Сколько формул в математике

Узнайте, сколько формул существует в математике. В этой статье мы рассмотрим различные виды формул и их применение в различных областях математики.

Математика — наука, которая изучает структуру, свойства и взаимосвязи чисел, величин и пространственных форм. Формулы являются неотъемлемой частью математики и используются для описания законов и зависимостей в различных областях знаний. От основных до сложных и неоднозначных, формулы предоставляют инструменты для решения различных задач.

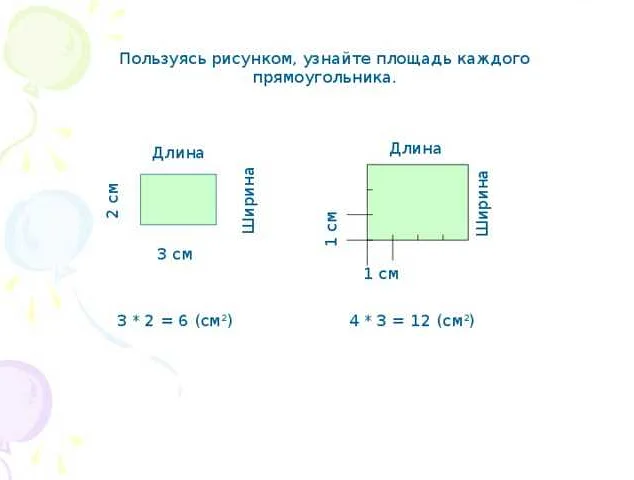
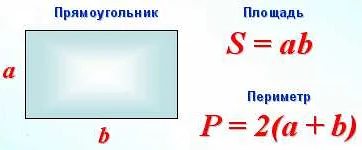
Основные формулы математики включают в себя такие понятия, как арифметические операции, геометрические фигуры, алгебраические уравнения и тригонометрические функции. Например, формула для вычисления площади прямоугольника — S = a * b, где S — площадь, а и b — длины сторон прямоугольника. Эта формула позволяет нам быстро рассчитать площадь прямоугольника, зная его размеры.

Сложные формулы в математике могут включать несколько переменных, функций и операций. Например, формула для нахождения процента скидки на товар — P = (1 — d) * 100%, где P — процент скидки, а d — десятичное представление скидки. Эта формула позволяет нам рассчитать процент скидки на товар, зная его цену и размер скидки в десятичной форме.

Важно помнить, что формулы в математике являются лишь инструментом для решения задач, и их использование требует понимания и правильной интерпретации. Некорректное применение формул может привести к ошибочным результатам и неверным выводам.

В конечном счете, количество формул в математике не может быть точно определено, так как оно зависит от области знаний и уровня сложности задачи. Однако, умение использовать формулы и понимать их суть является важным навыком для решения математических задач и применения математических концепций в реальной жизни.

Количество формул в математике: основные и сложные формулы для решения задач

В основе математики лежат базовые формулы, которые используются в широком спектре задач. Одной из таких формул является формула площади прямоугольника: S = a * b, где S – площадь, a и b – длины сторон прямоугольника.

Другой важной формулой является формула квадратного уравнения: x = (-b ± √(b^2 — 4ac)) / 2a, где x – корни уравнения, a, b и c – коэффициенты уравнения.

Вместе с базовыми формулами, в математике существуют и сложные формулы, которые применяются в специализированных областях. Например, в теории вероятностей используется формула условной вероятности: P(A|B) = P(A ∩ B) / P(B), где P(A|B) – условная вероятность события A при условии наступления события B.

Еще одной сложной формулой является формула дифференцирования: f'(x) = lim(h→0) (f(x+h) — f(x)) / h, где f'(x) – производная функции f(x).

Количество формул в математике огромно и постоянно растет с развитием науки. Основные формулы используются повсеместно и служат основой для решения различных задач. Сложные формулы позволяют решать более сложные и специализированные задачи в различных областях математики.

Использование формул в математике позволяет получать точные результаты и решать разнообразные задачи. Понимание основных и сложных формул является важным навыком для успешного изучения и применения математики.

Видео по теме:

Основные формулы для работы в математике

Формула вычитания: a — b = c, где a — уменьшаемое, b — вычитаемое, а c — разность.

Формула умножения: a * b = c, где a и b — множители, а c — произведение.

Формула деления: a / b = c, где a — делимое, b — делитель, а c — частное.

Формула квадратного корня: √a = b, где a — радиканд, а b — корень.

Формула площади прямоугольника: S = a * b, где a и b — длины сторон прямоугольника, а S — площадь.

Формула площади треугольника: S = (h * b) / 2, где h — высота, b — основание, а S — площадь.

Формула объема куба: V = a^3, где a — длина ребра, а V — объем.

Формула окружности: S = π * r^2, где π — число пи, r — радиус, а S — площадь.

Формула периметра круга: P = 2 * π * r, где π — число пи, r — радиус, а P — периметр.

Формула бинома Ньютона: (a + b)^n = C(n,0) * a^n * b^0 + C(n,1) * a^(n-1) * b^1 + … + C(n,n) * a^0 * b^n, где a и b — числа, n — степень, a^n — a в степени n, C(n,k) — биномиальный коэффициент.

Какие сложные формулы используются в математике

Одной из самых известных и сложных формул в математике является формула Гаусса для вычисления суммы чисел от 1 до n. Формула Гаусса выглядит следующим образом:

Формула Гаусса:	n(n + 1)
	—
	2

Эта формула позволяет быстро вычислить сумму всех натуральных чисел от 1 до n. Она широко применяется в различных областях математики, физики и информатики.

Еще одной сложной формулой, которую активно используют в математике, является формула Байеса. Формула Байеса используется для вычисления условной вероятности и является основой для статистического вывода. Она выглядит следующим образом:

Формула Байеса:

P(A|B) = (P(B|A) * P(A)) / P(B)

Эта формула позволяет вычислить вероятность наступления события A при условии, что произошло событие B. Она широко применяется в статистике, машинном обучении и искусственном интеллекте.

Кроме того, в математике существуют и другие сложные формулы, такие как формула Эйлера для вычисления комплексных чисел, формула Пи для вычисления площади круга, формула Ферма для нахождения наименьшего значения функции и многие другие. Все эти формулы играют важную роль в математике и применяются в различных областях науки и техники.

Вопрос-ответ:

Какие основные формулы есть в математике?

В математике существует множество основных формул, таких как формула для вычисления площади прямоугольника (S = a * b), формула для вычисления площади круга (S = π * r^2), формула для вычисления объема цилиндра (V = π * r^2 * h) и многие другие.

Какие сложные формулы используются в математике?

В математике существуют и сложные формулы, которые используются для решения более сложных задач. Например, для решения дифференциальных уравнений используются разностные формулы, для решения интегральных уравнений используются интегральные формулы, а для решения систем линейных уравнений используются матричные формулы.

Сколько всего формул в математике?

Точное количество формул в математике невозможно определить, так как их существует бесконечное множество. В математике разрабатывается и применяется новые формулы каждый день, поэтому невозможно узнать точное число.

Какие формулы используются в геометрии?

В геометрии используются различные формулы для вычисления площадей, объемов, длин отрезков и других характеристик геометрических фигур. Например, формулы для вычисления площади треугольника (S = 1/2 * a * h), площади параллелограмма (S = a * h), площади трапеции (S = 1/2 * (a + b) * h) и многие другие.

Какие формулы используются в физике?

В физике используются различные формулы для описания физических явлений. Например, формула для вычисления скорости (v = s / t), формула для вычисления работы (W = F * s * cos(α)), формула для вычисления энергии (E = m * c^2) и многие другие. Формулы в физике позволяют описывать и предсказывать поведение различных физических систем.

Какие основные формулы существуют в математике?

В математике существует множество основных формул, таких как формулы для расчета площади прямоугольника (S = a * b), площади круга (S = π * r^2), формулы для нахождения периметра (P = 2 * (a + b)), формулы для решения квадратного уравнения (x = (-b ± √(b^2 — 4ac)) / (2a)) и многие другие.

Зачем нужны формулы в математике

1. Формулы являются компактным и точным способом записи математических отношений и закономерностей. Они позволяют нам выразить сложные математические идеи и связи между разными величинами с помощью простых символов и операций.
2. Формулы помогают нам анализировать и понимать различные явления и процессы в мире. Они позволяют нам выявлять закономерности и устанавливать зависимости между разными переменными.
3. Формулы позволяют нам решать математические задачи. Они предоставляют нам инструменты для расчетов и построения моделей, которые помогают нам предсказывать и прогнозировать различные ситуации и результаты.
4. Формулы позволяют нам доказывать и устанавливать математические теоремы и утверждения. Они являются основой для математического рассуждения и доказательства.
5. Формулы помогают нам разрабатывать новые теории и расширять наши знания о мире. Они позволяют нам формулировать гипотезы и предположения, которые затем могут быть проверены и исследованы.

В целом, формулы играют важную роль в математике, так как они позволяют нам описывать, анализировать, решать и доказывать различные математические задачи и закономерности. Они являются основой для развития математической науки и ее применения в других областях знания и практики.

Примеры простых формул для решения задач

1. Формула площади прямоугольника: S = a * b, где S — площадь, a — длина одной из сторон, b — длина другой стороны. Эта формула позволяет найти площадь прямоугольника при известных значениях сторон.
2. Формула среднего арифметического: Среднее = (a + b + c) / 3, где Среднее — среднее арифметическое трех чисел a, b и c. При помощи этой формулы можно найти среднее значение из трех чисел.
3. Формула объема цилиндра: V = π * r^2 * h, где V — объем цилиндра, π — математическая константа Пи (примерное значение — 3.14), r — радиус основания цилиндра, h — высота цилиндра. При помощи этой формулы можно найти объем цилиндра при известных значениях радиуса и высоты.

Это всего лишь некоторые примеры простых формул, которые используются для решения различных задач в математике. Знание этих формул может значительно облегчить процесс решения задач и помочь получить точный ответ.

Какие формулы используются для решения сложных задач

Для решения сложных задач в математике используются различные формулы, которые позволяют выполнять сложные вычисления и находить нужные значения.

Ниже перечислены некоторые из основных формул, которые применяются для решения сложных задач в различных областях математики:

• Формулы для расчета площади и периметра геометрических фигур, таких как круг, треугольник, прямоугольник и т.д.
• Формулы для решения уравнений и систем уравнений, включая квадратные уравнения, линейные уравнения и т.д.
• Формулы для нахождения производных и интегралов в дифференциальном и интегральном исчислении, которые используются при изучении функций и их свойств.
• Формулы для вычисления вероятности и статистических характеристик, которые применяются в теории вероятностей и математической статистике.
• Формулы для решения задач по тригонометрии, включая тригонометрические функции, тригонометрические тождества и т.д.

Это лишь небольшая часть формул, которые могут быть использованы для решения сложных задач в математике. Каждая область математики имеет свои специфические формулы, которые применяются для решения задач в данной области.

Знание и применение этих формул позволяет упростить вычисления и решение сложных математических задач, а также облегчает понимание и изучение различных математических концепций.

Формулы для решения геометрических задач

Вот несколько основных формул, которые применяются при решении геометрических задач:

1. Формула для вычисления площади прямоугольника:

Площадь прямоугольника равна произведению его длины (a) на ширину (b):

S = a * b

2. Формула для вычисления площади круга:

Площадь круга равна произведению числа Пи (π) на квадрат радиуса (r):

S = π * r^2

3. Формула для вычисления объема цилиндра:

Объем цилиндра равен произведению площади основания (S) на высоту (h):

V = S * h

4. Формула для вычисления площади треугольника:

Площадь треугольника равна половине произведения длины основания (a) на высоту (h):

S = (1/2) * a * h

5. Формула для вычисления гипотенузы прямоугольного треугольника:

Гипотенуза (c) прямоугольного треугольника вычисляется по теореме Пифагора, согласно которой квадрат гипотенузы равен сумме квадратов катетов:

c^2 = a^2 + b^2

Это лишь некоторые из формул, которые применяются в геометрии для решения задач. Они позволяют находить площади, объемы, длины сторон и другие характеристики геометрических фигур и объектов. Знание и умение применять эти формулы облегчают решение задач и расширяют возможности геометрических вычислений.

Важные формулы для алгебры и арифметики

Формулы для арифметических операций

1. Формула сложения чисел: a + b = c, где a и b — слагаемые, а c — сумма.

2. Формула вычитания чисел: a — b = c, где a — уменьшаемое, b — вычитаемое, а c — разность.

3. Формула умножения чисел: a * b = c, где a и b — множители, а c — произведение.

4. Формула деления чисел: a / b = c, где a — делимое, b — делитель, а c — частное.

Формулы для решения уравнений

1. Формула линейного уравнения: ax + b = 0, где a и b — коэффициенты, а x — неизвестное.

2. Формула квадратного уравнения: ax^2 + bx + c = 0, где a, b и c — коэффициенты, а x — неизвестное.

3. Формула кубического уравнения: ax^3 + bx^2 + cx + d = 0, где a, b, c и d — коэффициенты, а x — неизвестное.

Формулы для работы с пропорциями

1. Формула пропорции: a/b = c/d, где a и c — соответственные части, а b и d — соответственные целые числа.

2. Формула пропорционального увеличения: a:b = c:d, где a и b — исходные значения, а c и d — новые значения.

Формулы для работы с процентами

1. Формула процентного соотношения: p% = p/100, где p — процент.

2. Формула расчета процента от числа: p% от a = (p/100) * a, где p — процент, а a — число.

3. Формула расчета числа при заданном проценте: a при p% = (a * 100) / p, где p — процент, а a — число.

Это лишь небольшой набор формул, которые широко применяются в алгебре и арифметике. Они помогают решать различные задачи и упрощать вычисления. Знание этих формул может быть полезно как в повседневной жизни, так и в профессиональной деятельности.

Сложные формулы для решения дифференциальных уравнений

Одним из наиболее сложных методов является метод вариации постоянных. Для его применения необходимо знание специальной формулы, которая позволяет решать линейные неоднородные дифференциальные уравнения.

Формула метода вариации постоянных имеет следующий вид:

1. Представляем общее решение неоднородного уравнения в виде суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.
2. Подставляем полученное представление в исходное неоднородное уравнение.
3. Определяем неизвестные постоянные, используя условия задачи.

Еще одной сложной формулой, используемой для решения дифференциальных уравнений, является формула Эйлера. Данная формула позволяет находить общее решение уравнения вида:

xny(n) + an-1xn-1y(n-1) + … + a0y = 0,

где n — натуральное число.

Формула Эйлера имеет следующий вид:

y = xr(c1ln(x) + c2),

где r — корень характеристического уравнения, а c1 и c2 — произвольные константы.

Это лишь две из множества сложных формул, используемых для решения дифференциальных уравнений. Знание и применение подобных формул позволяет решать задачи из разных областей науки и техники, где дифференциальные уравнения играют важную роль.