Что такое квадрат в математике определение

Квадратом в математике называется геометрическая фигура, у которой все стороны равны и все углы прямые. Квадрат также является специальным случаем прямоугольника, у которого все стороны равны. В математике квадрат также обозначает результат умножения числа на себя. Узнайте больше о квадрате и его свойствах в нашей статье.

Квадраты – это одно из основных понятий в математике, которое широко используется в различных областях. В математике квадратом называется результат умножения числа на себя. Например, квадрат числа 3 равен 9, так как 3 умноженное на 3 равно 9. Квадраты имеют множество интересных свойств и применений, которые делают их неотъемлемой частью математической науки.

Определение квадратов в математике является фундаментальным и важным для понимания более сложных математических понятий. Квадраты помогают нам изучать свойства чисел и решать разнообразные задачи. Они также являются основой для понимания кубов и других степеней чисел.

Применение квадратов в математике имеет широкий спектр. Они используются для решения уравнений, анализа графиков функций, построения геометрических фигур и многих других математических операций. Кроме того, квадраты играют важную роль в физике, экономике, программировании и других науках, где они помогают моделировать и предсказывать различные явления и процессы.

Квадраты в математике: основные понятия и определение

Квадраты играют важную роль в геометрии, алгебре и арифметике. В геометрии квадраты используются для изучения свойств фигур, решения задач на периметр и площадь, а также для построения различных геометрических моделей и диаграмм.

В алгебре квадраты также имеют свое определение. Квадрат числа — это результат умножения числа на себя. Например, квадрат числа 4 равен 4 умножить на 4, то есть 16.

Квадратные уравнения являются важным объектом изучения в алгебре. Они имеют вид ax^2 + bx + c = 0, где a, b и c — это коэффициенты, а x — неизвестная. Решение квадратного уравнения позволяет найти значения неизвестной x, при которых уравнение выполняется.

В арифметике квадраты используются для определения квадратного корня. Квадратный корень числа — это число, при возведении в квадрат которого получается исходное число. Например, квадратный корень из числа 9 равен 3, так как 3 умножить на 3 дает 9.

Таким образом, квадраты играют важную роль в математике и имеют много различных применений. Изучение квадратов позволяет углубить понимание геометрии, алгебры и арифметики, а также применять их в решении различных задач и уравнений.

Видео по теме:

История развития квадратов в математике

История использования квадратов в математике насчитывает свыше двух тысяч лет. Квадраты встречаются в различных сферах жизни и имеют важное значение в математике, астрономии, физике, инженерии и других науках.

В Древнем Египте и Древней Греции квадраты использовались для решения различных задач. Греческий математик Пифагор изучал свойства квадратов и ввел понятие квадратного корня. Позднее, в алгебре, математики использовали квадраты и квадратные корни для решения уравнений и анализа графиков функций.

В современной математике квадраты играют важную роль. Они используются в геометрии для определения площади квадрата и решения задач по теории вероятностей. Квадраты также используются в алгебре для решения систем уравнений и для анализа квадратных функций.

Квадраты имеют множество применений в реальной жизни. Они используются во многих инженерных и строительных расчетах. Кроме того, квадраты широко применяются в физике для измерения площадей, объемов и других величин.

Таким образом, история развития квадратов в математике свидетельствует о их важности и широком применении в различных областях знания.

Свойства квадратов: основные правила и законы

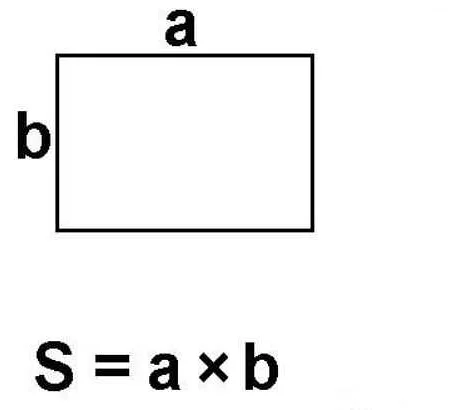
Основные правила и законы, связанные с квадратами, включают:

1. Стороны квадрата равны между собой. Это означает, что если известна длина одной стороны, то можно определить длину всех остальных сторон.
2. Квадрат имеет четыре прямых угла, каждый из которых равен 90 градусов.
3. Диагонали квадрата равны между собой и делят его на два прямоугольных треугольника.
4. Периметр квадрата вычисляется по формуле: П = 4 * a, где а — длина стороны квадрата.
5. Площадь квадрата вычисляется по формуле: S = a^2, где а — длина стороны квадрата.
6. Объем куба (трехмерного квадрата) вычисляется по формуле: V = a^3, где а — длина стороны куба.

Знание этих свойств и законов квадратов позволяет решать задачи различной сложности и упрощает работу с геометрическими фигурами, в которых используются квадраты.

Применение квадратов в алгебре и геометрии

Квадраты играют важную роль в алгебре и геометрии, предоставляя множество инструментов и методов для решения различных задач и проблем. В алгебре квадраты используются для выражения и упрощения алгебраических выражений, а также для решения уравнений и систем уравнений.

Одно из основных применений квадратов в алгебре — это вычисление квадратных корней. Квадратный корень из числа является таким числом, которое при возведении в квадрат дает исходное число. Квадратный корень может использоваться для нахождения неизвестных значений или для проверки правильности решений.

В геометрии квадраты играют важную роль при расчете площадей и периметров. Квадрат является особым видом прямоугольника, у которого все стороны равны. Это позволяет легко вычислять площадь и периметр квадрата, зная только длину одной его стороны.

Квадраты также используются в геометрии для моделирования различных объектов и фигур. Например, квадраты могут быть использованы для построения сетки координат или для создания графиков функций. Они также могут быть использованы для построения геометрических фигур, таких как кубы или пирамиды.

В обоих дисциплинах, алгебре и геометрии, квадраты играют важную роль и предоставляют мощный инструмент для решения различных задач. Понимание и использование квадратов позволяет упростить вычисления, решить уравнения и моделировать геометрические фигуры.

Квадратные уравнения: решение и примеры

Основной метод решения квадратных уравнений — формула дискриминанта. Дискриминант D вычисляется по формуле D = b^2 — 4ac. Значение дискриминанта позволяет определить тип решений уравнения:

• Если D > 0, то уравнение имеет два различных действительных корня.
• Если D = 0, то уравнение имеет один действительный корень.
• Если D < 0, то уравнение не имеет действительных корней, но имеет комплексные корни.

Примеры квадратных уравнений:

1. Уравнение x^2 — 5x + 6 = 0 имеет два корня: x1 = 2 и x2 = 3.
2. Уравнение 2x^2 + 4x + 2 = 0 имеет один корень: x = -1.
3. Уравнение 3x^2 + 2x + 5 = 0 не имеет действительных корней, но имеет комплексные корни.

Квадратные уравнения широко используются в различных областях математики и ее приложениях, таких как физика, экономика, инженерия и другие. Их решение позволяет найти значения переменных и решить задачи, связанные с пространственными и временными зависимостями.

Квадраты в планировании и конструкции

Квадраты часто используются в планировании и конструкции для измерения площади и создания симметричных форм.

В архитектуре и градостроительстве, квадраты помогают в определении пропорций и распределении пространства. Они используются для создания планов зданий и инфраструктурных объектов.

В строительстве, квадраты играют важную роль при расчете и планировании. Они помогают определить структуру и размеры строительных элементов, таких как стены, полы, потолки и окна.

Квадраты также используются в проектировании шаблонов и чертежей. Они помогают создать точные и симметричные формы, а также обеспечивают удобство в измерении и маркировке конструкции.

В области ландшафтного дизайна, квадраты используются для создания геометрических форм и организации пространства. Они помогают создать гармоничные и эстетически привлекательные композиции.

В целом, квадраты являются важным инструментом в планировании и конструкции, обеспечивая точность, пропорции и симметрию в процессе создания различных объектов и структур.

Квадраты в физике: применение и связь с другими величинами

Одним из основных применений квадратов в физике является описание кинематических величин, таких как скорость и ускорение. Например, квадрат скорости тела связан с его кинетической энергией и зависит от его массы и скорости. Также квадрат ускорения связан с изменением скорости тела и может быть использован для определения силы, действующей на тело.

Квадраты в физике также применяются для описания законов природы. Например, закон всемирного тяготения, согласно которому сила взаимодействия между двумя телами пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Это позволяет описать гравитационное взаимодействие и предсказывать движение небесных тел.

Кроме того, квадраты в физике используются для определения динамических величин, таких как работа и мощность. Например, работа, совершаемая силой, пропорциональна произведению силы и перемещения тела в квадрате, а мощность, определяемая как работа, совершаемая за единицу времени, зависит от работы и времени.

Таким образом, квадраты в физике играют важную роль в описании физических явлений и связи между различными величинами. Их использование позволяет проводить анализ и прогнозирование физических процессов, а также расширяет наши знания о мире и его законах.

Значение квадратов в повседневной жизни и практическом применении

Квадраты играют важную роль в математике и имеют различные применения в повседневной жизни. Они помогают нам решать задачи, моделировать реальные ситуации и понимать мир вокруг нас.

Вот несколько примеров, как квадраты используются в повседневной жизни:

1. Площади и периметры: Квадраты помогают нам вычислять площади и периметры различных фигур. Например, когда мы строим дом или учебное заведение, нам нужно знать площадь участка земли или площадь комнат, чтобы правильно планировать использование пространства.
2. Квадратные корни: В некоторых ситуациях нам нужно найти корень из числа. Например, при рассчете расстояния между двумя точками на плоскости или при определении длины стороны квадрата, если известна его площадь.
3. Геометрические формы: Квадраты — это одна из простейших геометрических фигур, которая имеет много свойств и характеристик. Они используются для создания других форм, таких как прямоугольники, кубы и прочие многогранники.
4. Квадраты в физике: В физике квадраты используются для измерения различных величин и вычисления физических законов. Например, для определения скорости, ускорения или энергии.

Это лишь некоторые примеры того, как квадраты находят свое применение в повседневной жизни и практических задачах. Они не только помогают упростить вычисления и решение задач, но и расширяют наше понимание мира вокруг нас.

Вопрос-ответ:

Что такое квадрат в математике?

В математике квадрат — это число, возведенное во вторую степень.

Как определить квадрат числа?

Чтобы определить квадрат числа, нужно это число возвести во вторую степень.

Какие свойства имеют квадраты чисел?

Квадраты чисел положительны или равны нулю, они могут быть использованы для измерения площадей, а также являются основой для формулы пифагорова.

Какие применения имеют квадраты в математике?

Квадраты используются для решения задач, связанных с площадями, геометрией, алгеброй и физикой. Они позволяют нам находить площади фигур, решать уравнения и моделировать реальные явления.