Что такое подмножество в математике

Подмножество в математике — это набор элементов, которые являются частью другого набора. Узнайте, как определить подмножество и как оно связано с понятием множества в математике.

В математике подмножество — это понятие, которое используется для описания отношений между множествами. Подмножество определяется как множество, содержащееся внутри другого множества. Другими словами, каждый элемент подмножества также является элементом данного множества. Подмножество может содержать все элементы исходного множества или только некоторые из них.

Для обозначения подмножества используется символ «⊆». Например, если A и B — два множества, и все элементы множества A также являются элементами множества B, то можно записать это как A ⊆ B. Если множество A является подмножеством множества B, но оно не является равным множеству B, то запись будет выглядеть как A ⊂ B.

Примером подмножества может служить множество всех четных чисел, которое является подмножеством множества всех целых чисел. Также можно рассмотреть множество всех трехзначных чисел, которое является подмножеством множества всех натуральных чисел.

Подмножество играет важную роль в математике и других науках. Оно позволяет определить отношения между множествами и использовать их в решении различных задач.

Определение подмножества в математике: понятие и суть

Пусть A и B — два множества. Если каждый элемент множества A также является элементом множества B, то говорят, что A является подмножеством B. Обозначение для подмножества — A ⊆ B.

Понятие подмножества позволяет строить иерархическую структуру множеств. Если множество A является подмножеством множества B, то можно говорить о включении A в B. Например, множество всех кругов является подмножеством множества всех фигур, так как каждый круг также является фигурой.

Определение подмножества в математике играет важную роль во многих областях, включая теорию множеств, логику, алгебру и дискретную математику. Понятие подмножества также используется в других науках, таких как информатика и физика, для описания отношений между объектами и сущностями.

Видео по теме:

Подмножество: что это и зачем оно нужно

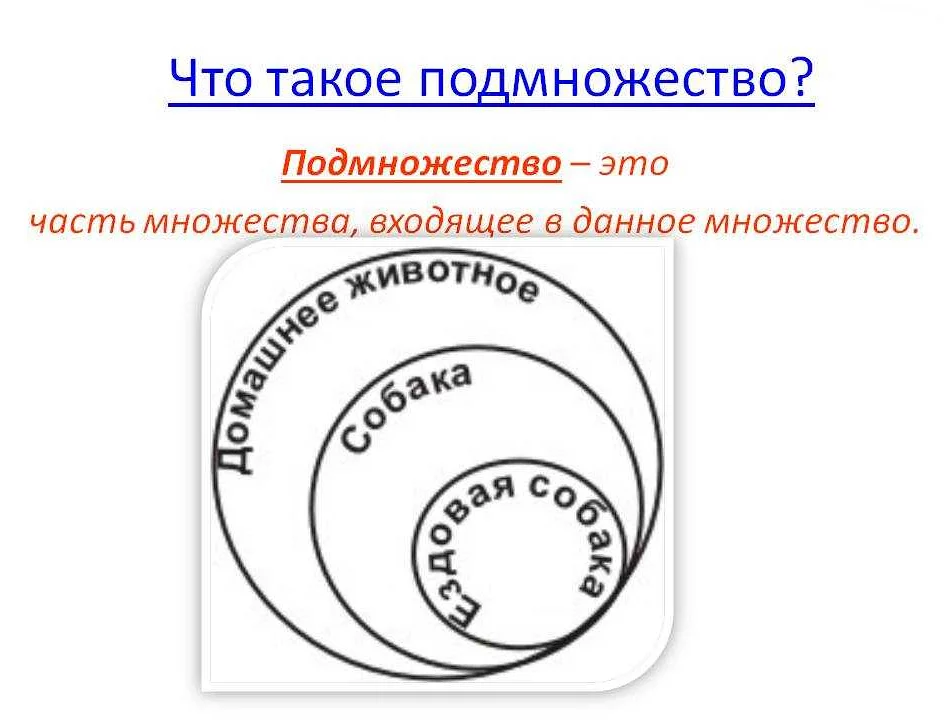
Зачем нужно понятие подмножества? Оно позволяет нам строить отношения и классификации между множествами. Мы можем сравнивать множества, устанавливать, является ли одно множество подмножеством другого, и делать выводы на основе этих отношений.

Например, рассмотрим множества A = {1, 2, 3} и B = {1, 2, 3, 4, 5}. В данном случае множество A является подмножеством множества B, так как все элементы множества A также присутствуют в множестве B. Мы можем записать это формально следующим образом: A ⊆ B.

Понятие подмножества также полезно при решении задач на пересечение и объединение множеств. Если мы знаем, что одно множество является подмножеством другого, то мы можем использовать это знание для упрощения решения задач и получения более точных результатов.

Таким образом, понятие подмножества играет важную роль в математике, позволяя нам устанавливать отношения между множествами и использовать эти отношения для решения различных задач.

Основные свойства и характеристики подмножества

Основные свойства и характеристики подмножества включают:

Символ	Описание
A ⊆ B	Множество A является подмножеством множества B
A ⊂ B	Множество A является строгим подмножеством множества B (A ≠ B)
A ⊄ B	Множество A не является подмножеством множества B
∅ ⊆ A	Пустое множество является подмножеством любого множества
A ⊆ A	Любое множество является подмножеством самого себя

Символ ⊆ обозначает отношение подмножества. Если A ⊆ B, то говорят, что A содержится в B. Если A ⊂ B, то A содержится строго в B.

Также стоит отметить, что любое множество является подмножеством самого себя, а пустое множество является подмножеством любого множества.

Подмножества играют важную роль в математике и широко применяются в различных областях, включая теорию множеств, логику, алгебру и геометрию.

Вопрос-ответ:

Что такое подмножество в математике?

Подмножество в математике — это часть множества, состоящая из некоторых или всех его элементов. Если каждый элемент множества A также является элементом множества B, то говорят, что A является подмножеством B.

Как определить подмножество?

Для определения подмножества нужно проверить, что каждый элемент множества A также является элементом множества B. Если это условие выполняется, то множество A является подмножеством множества B.

Может ли пустое множество быть подмножеством?

Да, пустое множество является подмножеством любого другого множества. Так как в пустом множестве нет элементов, то каждый элемент любого другого множества будет также являться элементом пустого множества.

Какие примеры можно привести подмножеств?

Примеры подмножеств можно привести в различных областях математики. Например, в множестве натуральных чисел можно рассмотреть подмножество четных чисел или подмножество простых чисел. В множестве геометрических фигур можно рассмотреть подмножество квадратов или подмножество треугольников. Примеры подмножеств можно найти во многих других областях математики.

Примеры подмножества: известные иллюстрации

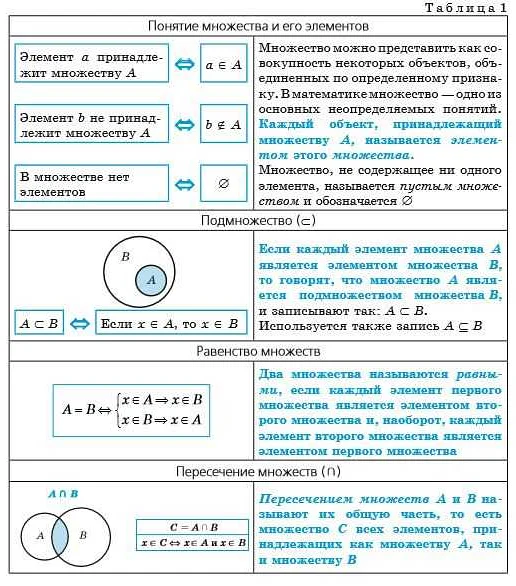
Рассмотрим несколько примеров подмножеств, чтобы лучше понять их суть:

• Пусть у нас есть множество A, состоящее из всех целых чисел от 1 до 5. Тогда подмножество B может быть множеством всех четных чисел в A: B={2, 4}. В этом случае B является подмножеством множества A.
• Рассмотрим множество C, состоящее из всех книг в библиотеке. Подмножеством C может быть множество D, которое состоит только из книг по математике: D={Алгебра, Геометрия}. Здесь D является подмножеством множества C.
• Пусть у нас есть множество E, состоящее из всех точек на координатной плоскости. Подмножество F может быть множеством точек, которые лежат на оси OX: F={(1, 0), (2, 0), (3, 0)}. В этом случае F является подмножеством множества E.

Это лишь некоторые примеры подмножеств, которые помогают наглядно представить, как они работают в математике. Важно помнить, что подмножество — это часть множества, которая включает в себя некоторые, а возможно и все элементы исходного множества.

Различные виды подмножеств и их классификация

В математике подмножества могут быть классифицированы по различным признакам. Рассмотрим некоторые из них:

• Пустое множество: это подмножество, не содержащее ни одного элемента. Оно обозначается символом ∅ или {}.
• Единичное множество: это подмножество, содержащее только один элемент. Например, {1} или {a}.
• Конечное множество: это подмножество, содержащее конечное количество элементов. Например, {1, 2, 3} или {a, b, c}.
• Бесконечное множество: это подмножество, содержащее бесконечное количество элементов. Например, {1, 2, 3, …} или {a, b, c, …}.
• Простое множество: это подмножество, в котором все элементы уникальны. Например, {1, 2, 3} или {a, b, c}.
• Составное множество: это подмножество, в котором содержатся повторяющиеся элементы. Например, {1, 2, 2, 3} или {a, a, b, c}.
• Исключительное множество: это подмножество, которое содержит элементы только из одного основного множества, и не содержит элементов из других множеств. Например, A = {1, 2, 3} и B = {3, 4, 5}, исключительное множество C = {1, 2} будет содержать только элементы из множества A, но не из множества B.
• Универсальное множество: это основное множество, которое содержит все возможные элементы, рассматриваемые в данном контексте. Оно обозначается символом U. Например, если рассматривается множество всех натуральных чисел, то универсальное множество будет обозначаться как U = {1, 2, 3, …}.

Это лишь некоторые из возможных классификаций подмножеств. В математике есть и другие классификации, которые могут быть использованы для более детального изучения свойств и отношений между подмножествами.

Отношения и операции с подмножествами

В математике существуют различные отношения и операции, которые могут быть применены к подмножествам.

С одной стороны, отношения позволяют сравнивать и устанавливать связи между различными подмножествами. Например, можно проверять, является ли одно подмножество частью другого, или наоборот. Такие отношения обычно обозначаются символами ⊆ (подмножество) и ⊂ (собственное подмножество). Например, если множество A содержит все элементы множества B, то говорят, что B является подмножеством A, и записывается как B ⊆ A. Если при этом множество A содержит хотя бы один элемент, которого нет в B, то говорят, что B является собственным подмножеством A, и записывается как B ⊂ A.

С другой стороны, операции с подмножествами позволяют создавать новые подмножества на основе уже существующих. Существуют три основные операции с подмножествами:

• Объединение: объединение двух подмножеств A и B образует новое подмножество, которое содержит все элементы их объединения. Обозначается символом ∪. Например, если A = {1, 2} и B = {2, 3}, то их объединение A ∪ B = {1, 2, 3}.
• Пересечение: пересечение двух подмножеств A и B образует новое подмножество, которое содержит только те элементы, которые принадлежат обоим подмножествам. Обозначается символом ∩. Например, если A = {1, 2} и B = {2, 3}, то их пересечение A ∩ B = {2}.
• Разность: разность двух подмножеств A и B образует новое подмножество, которое содержит только те элементы, которые принадлежат A, но не принадлежат B. Обозначается символом −. Например, если A = {1, 2} и B = {2, 3}, то их разность A − B = {1}.

Эти операции позволяют строить более сложные множества на основе уже имеющихся подмножеств и проводить различные операции с ними, что является важным инструментом в математике и других областях науки.

Роль и применение подмножеств в математике и других областях

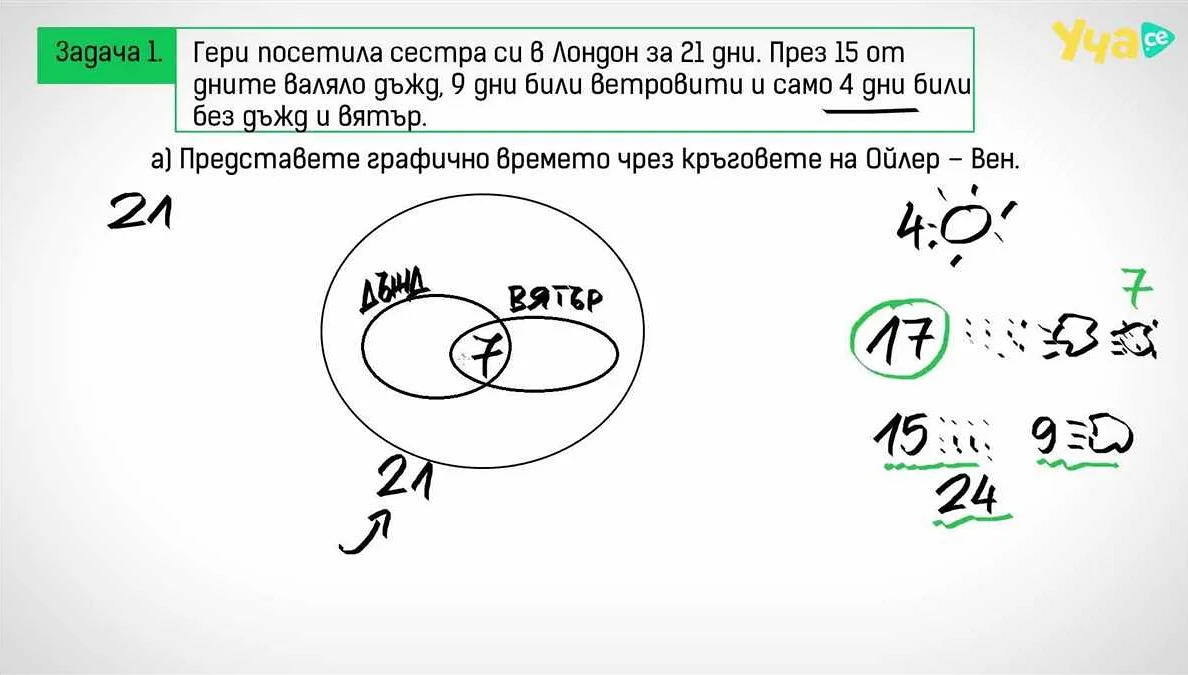
Подмножества играют важную роль в математике и других областях, таких как логика, информатика, теория множеств и даже в практической жизни. Они используются для описания и классификации объектов, установления отношений между ними, а также для решения различных задач.

В математике подмножества являются одним из основных понятий и составляют основу теории множеств. Они позволяют классифицировать и сравнивать множества по их элементам. Например, подмножество натуральных чисел может быть множеством четных чисел. Подмножества также используются для определения отношений между множествами, таких как включение и пересечение.

В логике подмножества используются для описания и классификации множеств высказываний. Например, множество «любые животные» может быть подмножеством множества «любые млекопитающие». Подмножества также позволяют устанавливать отношения между высказываниями, такие как подмножества «истинных высказываний» и «ложных высказываний».

В информатике подмножества используются для организации и классификации данных. Например, в базах данных можно использовать подмножества для описания групп объектов с общими свойствами. Подмножества также позволяют определить отношения между данными, такие как «подмножество всех пользователей, имеющих доступ к определенному ресурсу».

В практической жизни подмножества могут использоваться для классификации и организации объектов. Например, подмножество «различные виды фруктов» может быть использовано для классификации различных фруктов по их видам. Подмножества также помогают определить отношения между объектами, такие как «подмножество товаров, доступных для покупки в определенном магазине».

Таким образом, подмножества играют важную роль в различных областях и позволяют описывать, классифицировать и устанавливать отношения между объектами. Они являются основным инструментом для работы с множествами и являются неотъемлемой частью математики и других наук.

Связь подмножеств с другими математическими понятиями

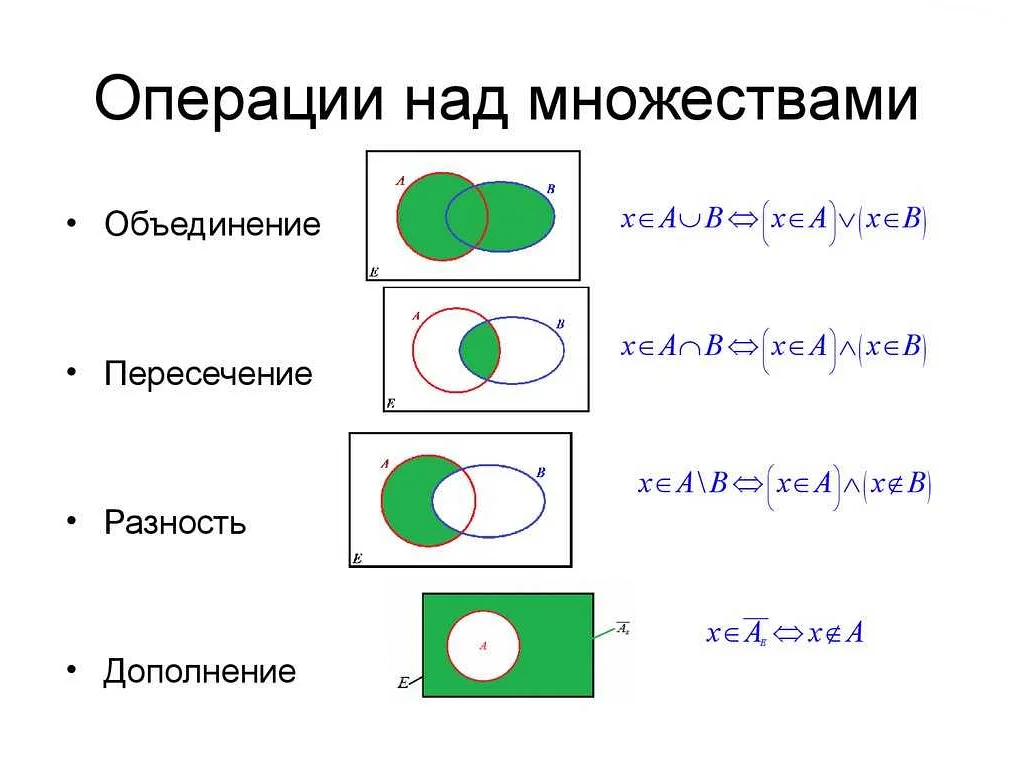
• Пересечение множеств: Если множество A является подмножеством множества B, то пересечение множеств A и B будет равно множеству A.
• Объединение множеств: Если множество A является подмножеством множества B, то объединение множеств A и B будет равно множеству B.
• Равенство множеств: Если множество A является подмножеством множества B и множество B является подмножеством множества A, то множества A и B равны.
• Дополнение множества: Если множество A является подмножеством множества B, то дополнение множества A относительно множества B будет равно разности множеств B и A.
• Выражение через символы: Подмножество может быть выражено математическим обозначением с использованием символа «⊆». Например, если множество A является подмножеством множества B, то можно записать «A ⊆ B».

Это лишь некоторые примеры связи подмножеств с другими математическими понятиями. Понимание и использование понятия подмножества позволяет более глубоко изучать и применять различные области математики.

Выводы о значимости и практическом применении подмножеств

Одним из главных применений подмножеств является классификация и группировка объектов в различных областях знания. Например, в компьютерной науке подмножества используются для описания иерархии классов и наследования в объектно-ориентированном программировании.

Подмножества также играют важную роль в теории множеств, где они используются для формулирования и доказательства различных теорем и утверждений. Они позволяют строить логические цепочки и выводы, а также определять отношения между множествами.

Кроме того, понятие подмножества имеет практическое применение в различных областях, таких как теория вероятностей, экономика, социология и другие. Например, в теории вероятностей подмножества используются для описания событий и определения вероятности их возникновения.

Таким образом, понимание и использование понятия подмножеств является важным элементом в математике и его применении в практике. Оно позволяет строить логические цепочки и доказательства, классифицировать и группировать объекты, а также формулировать и решать различные задачи в различных областях знания.