Что такое подмножество в математике 5 класс

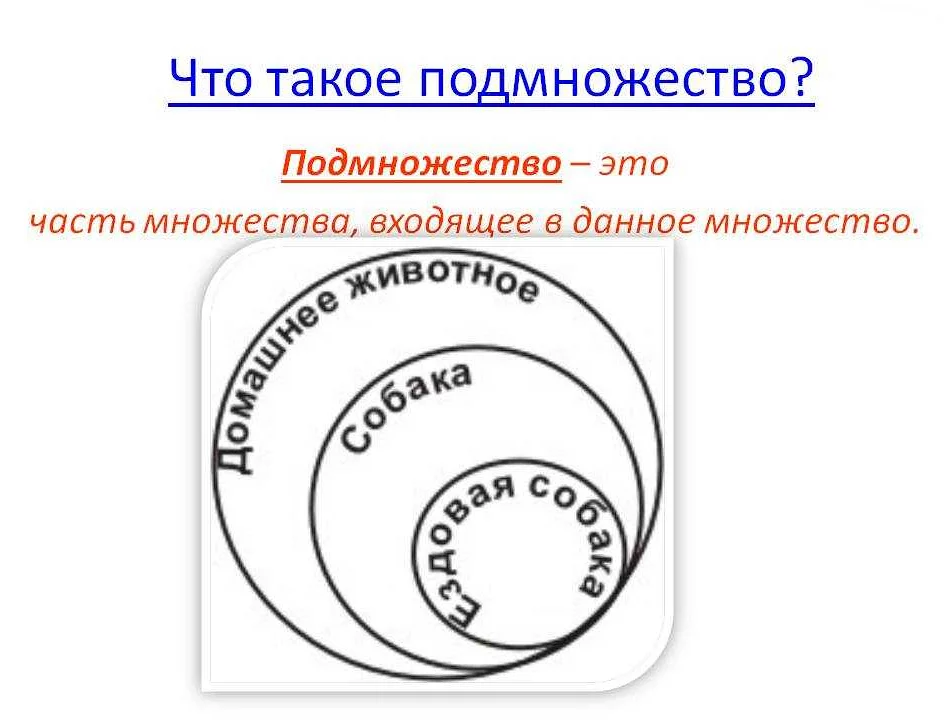
Подмножество в математике 5 класс — это часть множества, состоящая из некоторых его элементов. Узнайте основные понятия и правила работы с подмножествами в пятом классе математики.

В математике, подмножество — это группа элементов, которые являются частью более общего множества. Подмножество содержит только те элементы, которые находятся в исходном множестве. Таким образом, каждый элемент подмножества является элементом исходного множества.

Определение подмножества может быть наглядно проиллюстрировано с помощью примера. Рассмотрим множество натуральных чисел от 1 до 10 — {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Возьмем подмножество этого множества, состоящее только из четных чисел — {2, 4, 6, 8, 10}. В данном случае подмножество четных чисел является подмножеством множества натуральных чисел от 1 до 10.

Подмножества играют важную роль в математике и имеют множество применений. Они помогают разбивать большие множества на более мелкие группы для более удобной работы. Кроме того, подмножества используются для описания отношений и связей между элементами множества.

Например, рассмотрим множество всех студентов в классе. Мы можем выделить подмножество, состоящее только из студентов, которые занимаются спортом. Это позволит нам изучить и анализировать особенности и характеристики именно этой группы студентов, не затрагивая остальных.

Таким образом, понимание понятия подмножества в математике 5 класс позволяет нам более глубоко изучать и анализировать различные группы элементов, а также строить логические связи и отношения между ними.

Подмножество в математике 5 класс

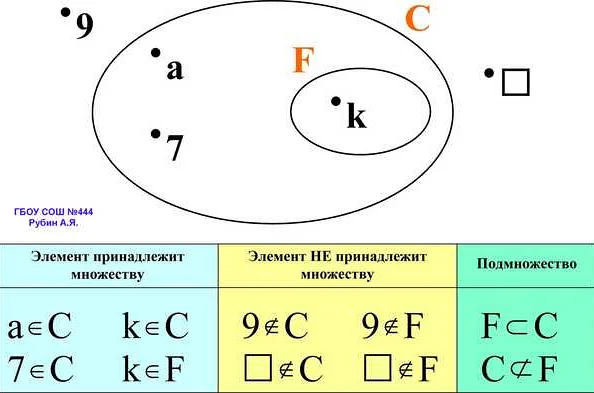
Обозначение подмножества: A ⊆ B. Если множество A не является подмножеством множества B, то обозначение будет: A ⊈ B.

В математике 5 класса часто встречаются примеры использования подмножеств. Например, можно рассмотреть множество всех животных и подмножества этого множества, такие как множество всех собак или множество всех кошек. Каждое из этих подмножеств является подмножеством множества всех животных.

Множество AМножество BПодмножество (A ⊆ B)

{1, 2}	{1, 2, 3, 4, 5}	Да
{1, 2, 6}	{1, 2, 3, 4, 5}	Нет
{apple, banana}	{apple, orange, banana}	Да

В приведенной таблице показаны примеры подмножеств. Множество A является подмножеством множества B, если все элементы множества A также являются элементами множества B.

Видео по теме:

Определение подмножества

Обозначение подмножества: A ⊆ B, где A — подмножество, а B — множество, в котором оно содержится. Если A не является подмножеством B, то обозначается как A ⊈ B.

Подмножество может быть как конечным, так и бесконечным. Например, множество натуральных чисел является подмножеством множества целых чисел.

Важно отличать понятие подмножества от понятия собственного подмножества. Собственное подмножество — это подмножество, которое не совпадает с исходным множеством. Например, если множество A = {1, 2, 3} и множество B = {1, 2, 3, 4, 5}, то A является собственным подмножеством B, потому что A ≠ B.

Примеры подмножеств

В математике подмножествами множества A называются все его части, включая само множество A и пустое множество.

Например, если у нас есть множество A = {1, 2, 3}, то его подмножествами будут:

1) Пустое множество ∅

2) Множество {1}

3) Множество {2}

4) Множество {3}

5) Множество {1, 2}

6) Множество {1, 3}

7) Множество {2, 3}

8) Множество {1, 2, 3} (само множество A).

Таким образом, в данном примере у множества A есть 8 подмножеств.

Заметим, что любое множество является подмножеством самого себя, а пустое множество является подмножеством любого множества.

Вопрос-ответ:

Что такое подмножество?

Подмножество — это набор элементов, включенных в другое множество.

Чем отличается подмножество от множества?

Подмножество — это множество, элементы которого включены в другое множество. Множество же — это набор уникальных элементов.

Как определить подмножество?

Для определения подмножества нужно проверить, что все элементы данного набора также включены в другое множество.

Какие примеры подмножеств можно привести?

Примерами подмножеств могут быть: множество всех четных чисел, множество всех красных фруктов, множество всех студентов в определенном классе и т.д.

Какие свойства имеют подмножества?

Подмножества обладают следующими свойствами: любое множество является подмножеством самого себя, пустое множество является подмножеством любого множества, количество подмножеств конечного множества равно 2 в степени количества элементов в множестве и т.д.

Что такое подмножество в математике?

Подмножество — это множество, элементы которого являются частью другого множества. То есть, если все элементы множества А также являются элементами множества В, то множество А является подмножеством множества В.

Как можно определить подмножество?

Для определения того, является ли одно множество подмножеством другого, необходимо проверить, что все элементы первого множества также являются элементами второго множества. Если это условие выполняется, то первое множество является подмножеством второго.

Равные множества

Для того чтобы два множества были равными, все их элементы должны совпадать. Порядок элементов в множестве не имеет значения. Например, множества {1, 2, 3} и {3, 2, 1} являются равными, так как содержат одни и те же элементы.

Равные множества можно обозначать с помощью знака равенства (=). Например, если множество A = {1, 2, 3} и множество B = {3, 2, 1}, то можно записать A = B, что означает, что множества A и B равны.

Равные множества важны для понимания операций над множествами, таких как объединение, пересечение и разность. Если два множества равны, то результаты этих операций также будут равными.

Например, если множество A = {1, 2, 3} и множество B = {3, 2, 1}, то:

• Объединение множеств A и B будет равно A ∪ B = {1, 2, 3} ∪ {3, 2, 1} = {1, 2, 3}
• Пересечение множеств A и B будет равно A ∩ B = {1, 2, 3} ∩ {3, 2, 1} = {1, 2, 3}
• Разность множеств A и B будет равна A \ B = {1, 2, 3} \ {3, 2, 1} = {} (пустое множество)

Таким образом, равные множества играют важную роль в математике и позволяют нам устанавливать соответствие между различными множествами и выполнять различные операции над ними.

Пустое множество

Пустое множество является особенным, так как оно является подмножеством любого другого множества. Например, если рассмотреть множество всех четных чисел, то пустое множество будет его подмножеством, так как в нем нет ни одного элемента, которое не является четным.

Пустое множество используется, например, в теории множеств для формулирования аксиом или определений. Оно также может использоваться в математике для обозначения невозможности выполнения какого-либо условия или отсутствия элементов, удовлетворяющих определенным требованиям.

Собственные подмножества

Собственным подмножеством множества А называется такое подмножество B, которое содержит только некоторые элементы множества А, но при этом не равно ему.

Например, пусть множество А = {1, 2, 3, 4}. Тогда собственными подмножествами множества А будут:

• {1}
• {2}
• {3}
• {4}
• {1, 2}
• {2, 3}
• {3, 4}
• {1, 3}
• {2, 4}

Эти подмножества содержат только некоторые элементы множества А, но не равны ему.

Собственные подмножества являются важным понятием в теории множеств и используются для решения различных задач, в том числе в математическом анализе и дискретной математике.

Количество подмножеств

Для множества, содержащего n элементов, количество подмножеств равно 2^n. Это означает, что каждый элемент может присутствовать или отсутствовать в каждом подмножестве. Всего имеется 2^n возможных комбинаций.

Например, для множества {1, 2, 3} количество подмножеств будет равно 2^3 = 8. Все возможные подмножества данного множества: {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}.

Таблица ниже показывает количество подмножеств для различных значений n:

nКоличество подмножеств (2^n)

0	1
1	2
2	4
3	8
4	16

Таким образом, количество подмножеств для множества зависит от количества его элементов и равно 2^n, где n — количество элементов в множестве.

Операции над подмножествами

В математике существуют различные операции, которые можно выполнять над подмножествами. Рассмотрим основные из них:

• Объединение подмножеств — это операция, которая позволяет объединить все элементы двух или более подмножеств в одно подмножество. Обозначается символом «∪». Например, если имеются два подмножества A = {1, 2, 3} и B = {3, 4, 5}, то их объединение будет выглядеть так: A ∪ B = {1, 2, 3, 4, 5}.
• Пересечение подмножеств — это операция, которая позволяет найти все общие элементы двух или более подмножеств. Обозначается символом «∩». Например, если имеются два подмножества A = {1, 2, 3} и B = {3, 4, 5}, то их пересечение будет выглядеть так: A ∩ B = {3}.
• Разность подмножеств — это операция, которая позволяет найти все элементы одного подмножества, которых нет в другом подмножестве. Обозначается символом «\» или «-«. Например, если имеются два подмножества A = {1, 2, 3} и B = {3, 4, 5}, то их разность будет выглядеть так: A \ B = {1, 2}.
• Дополнение подмножества — это операция, которая позволяет найти все элементы, которых нет в заданном подмножестве, относительно некоторого универсального множества. Обозначается символом «‘». Например, если имеется подмножество A = {1, 2, 3}, а универсальное множество U = {1, 2, 3, 4, 5}, то дополнение подмножества A относительно множества U будет выглядеть так: A’ = {4, 5}.

Эти операции могут быть полезными при работе с подмножествами и позволяют выполнять различные действия над элементами множеств.

Подмножество и включение

Для определения подмножества, необходимо проверить, что каждый элемент множества A является элементом множества B. Если это так, то A является подмножеством B, в противном случае A не является подмножеством B.

Например, рассмотрим множество A = {1, 2, 3} и множество B = {1, 2, 3, 4, 5}. В данном случае, каждый элемент множества A также присутствует в множестве B, поэтому A является подмножеством B.

Множество AМножество BA ⊆ B

{1, 2, 3}

{1, 2, 3, 4, 5}

Да