Что значит множество в математике

Множество в математике – это совокупность элементов, объединенных общим признаком или свойством. В данной статье рассмотрены основные понятия и определения, связанные с множествами, а также приведены примеры их использования в математических задачах и теориях. Узнайте, что такое пустое множество, подмножество, объединение и пересечение множеств, а также какие операции и свойства связаны с множествами в математике.

Множество — одно из основных понятий математики, которое является фундаментом для построения всех других математических объектов. Множество представляет собой совокупность элементов, объединенных общим свойством или условием. Элементы множества могут быть любыми объектами: числами, буквами, словами, геометрическими фигурами и т.д.

Множество обычно обозначается заглавными буквами, например, A, B, C и т.д. Элементы множества записываются внутри фигурных скобок и разделяются запятыми. Например, множество натуральных чисел можно записать так: {1, 2, 3, 4, …}.

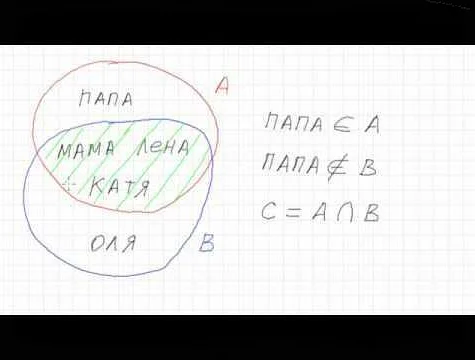
Принадлежность элемента к множеству обозначается символом ∈ (принадлежит) или ∉ (не принадлежит). Например, если A = {1, 2, 3} и B = {2, 3, 4}, то 2 ∈ A и 4 ∉ A.

Множества могут быть конечными или бесконечными. Конечное множество содержит конечное число элементов, а бесконечное множество имеет бесконечное число элементов. Например, множество всех целых чисел является бесконечным.

Множества могут быть пустыми, то есть не содержать ни одного элемента, и обозначаются символом ∅ или {}.

Что такое множество в математике

Основные свойства множества:

1. Элементы множества могут быть перечислены внутри фигурных скобок {} через запятую. Например, множество натуральных чисел можно записать как {1, 2, 3, …}.
2. Множество не имеет повторяющихся элементов. Каждый элемент может присутствовать в множестве только один раз.
3. Порядок элементов в множестве не имеет значения. Например, множества {1, 2, 3} и {3, 2, 1} считаются одинаковыми.

Множество может быть конечным или бесконечным. Конечное множество содержит определенное количество элементов, например, множество {1, 2, 3}. Бесконечное множество содержит несчетное количество элементов, например, множество натуральных чисел.

Множество может быть пустым, то есть не содержать ни одного элемента. Пустое множество обозначается символом ∅ или {}.

Примеры множеств:

Множество натуральных чисел: N = {1, 2, 3, …}

Множество целых чисел: Z = {…, -3, -2, -1, 0, 1, 2, 3, …}

Множество рациональных чисел: Q = {x | x = p/q, p ∈ Z, q ∈ Z, q ≠ 0}

Множество действительных чисел: R = {x | x — любое действительное число}

Множество комплексных чисел: C = {x + yi | x, y — действительные числа, i — мнимая единица}

Определение и основные понятия

Основные понятия, связанные с множествами:

• Элемент: отдельный объект или число, принадлежащий множеству.
• Пустое множество: множество, не содержащее ни одного элемента. Обозначается как ∅ или {}.
• Конечное множество: множество, состоящее из конечного числа элементов.
• Бесконечное множество: множество, состоящее из бесконечного числа элементов.
• Равенство множеств: два множества считаются равными, если они содержат одни и те же элементы.
• Подмножество: множество A является подмножеством множества B, если каждый элемент A также является элементом B.
• Декартово произведение: множество всех возможных упорядоченных пар элементов из двух множеств.

Это основные понятия, которые используются при работе с множествами в математике. Они являются основой для более сложных операций и свойств множеств, которые рассматриваются в дальнейшем.

Свойства множества

Множество в математике обладает рядом важных свойств, которые характеризуют его:

СвойствоОписание

Элементарность	Множество состоит из отдельных элементов, которые называются его членами или элементами. Любой объект может быть членом множества или не быть им.
Уникальность	В множестве не может быть повторяющихся элементов. Каждый элемент может встречаться в множестве только один раз.
Порядок	Порядок элементов в множестве не имеет значения. Это означает, что множество {1, 2, 3} и множество {3, 2, 1} считаются одним и тем же множеством.
Размерность	Мощность множества определяется количеством его элементов. Если множество содержит конечное число элементов, то его мощность называется конечной. Если же множество содержит бесконечное число элементов, то его мощность называется бесконечной.
Включение	Множество может быть включено в другое множество. Если каждый элемент одного множества является элементом другого множества, то первое множество называется подмножеством второго.
Операции	Существуют различные операции над множествами, такие как объединение, пересечение, разность, симметрическая разность и декартово произведение. Они позволяют комбинировать и преобразовывать множества.

Эти свойства помогают определить и изучить различные аспекты множеств в математике.

Равенство и подмножество

Два множества считаются равными, если они содержат одни и те же элементы. Если каждый элемент первого множества также является элементом второго множества, и наоборот, то эти множества считаются равными. Равенство множеств обозначается символом «=».

Подмножество — это отношение между двумя множествами, при котором каждый элемент первого множества также является элементом второго множества. Если множество A является подмножеством множества B, то записывается как A ⊆ B. Если существует элемент, который принадлежит множеству A, но не принадлежит множеству B, то множество A не является подмножеством множества B.

Понятие подмножества также включает понятие собственного подмножества. Собственное подмножество — это подмножество, которое содержит хотя бы один элемент, не принадлежащий рассматриваемому множеству.

Множество AМножество BРезультат

{1, 2, 3}	{1, 2, 3}	A = B
{1, 2}	{1, 2, 3}	A ⊆ B
{1, 2, 3}	{1, 2}	B ⊆ A
{1, 2}	{1, 2, 3}	A ≠ B
{1, 2, 3}	{1, 2}	A ⊂ B
{1, 2}	{1, 2, 3}	B ⊃ A

Операции над множествами

Множества в математике поддерживают различные операции, которые позволяют выполнять действия над элементами множеств. Операции над множествами включают:

1. Объединение множеств: объединение двух множеств включает все элементы из обоих множеств без повторений. Обозначается символом «∪». Например, объединение множеств {1, 2, 3} и {3, 4, 5} равно {1, 2, 3, 4, 5}.
2. Пересечение множеств: пересечение двух множеств включает только те элементы, которые присутствуют и в первом, и во втором множестве. Обозначается символом «∩». Например, пересечение множеств {1, 2, 3} и {3, 4, 5} равно {3}.
3. Разность множеств: разность двух множеств включает все элементы, которые присутствуют в первом множестве, но отсутствуют во втором множестве. Обозначается символом «\» или «-«. Например, разность множеств {1, 2, 3} и {3, 4, 5} равна {1, 2}.
4. Симметрическая разность множеств: симметрическая разность двух множеств включает все элементы, которые присутствуют только в одном из множеств. Обозначается символом «△». Например, симметрическая разность множеств {1, 2, 3} и {3, 4, 5} равна {1, 2, 4, 5}.

Эти операции позволяют строить новые множества на основе уже заданных, а также производить сравнение и анализ множеств. Они являются основными инструментами работы с множествами в математике и других областях, где множества используются для решения задач.

Примеры множеств

ПримерОписание

Множество натуральных чисел	Множество всех положительных целых чисел, начиная с единицы.
Множество целых чисел	Множество всех положительных и отрицательных целых чисел, включая ноль.
Множество рациональных чисел	Множество всех чисел, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами.
Множество действительных чисел	Множество всех чисел, которые можно представить на числовой прямой.
Множество комплексных чисел	Множество всех чисел, которые можно представить в виде суммы действительной и мнимой частей.
Множество простых чисел	Множество всех натуральных чисел, имеющих ровно два делителя: 1 и само число.

Это лишь некоторые примеры множеств, которые встречаются в математике. Множества могут быть бесконечными или конечными, содержать различные элементы и иметь свои уникальные свойства.

Бесконечные множества

В математике существуют множества, которые содержат несчетное количество элементов и называются бесконечными множествами. Они играют важную роль в различных областях математики и имеют множество интересных свойств и особенностей.

Одним из примеров бесконечных множеств является множество натуральных чисел. Это множество содержит все положительные целые числа, начиная с 1, и таким образом, его количество элементов бесконечно.

Еще одним примером бесконечного множества является множество всех целых чисел. Оно содержит как положительные, так и отрицательные целые числа, и, следовательно, имеет несчетное количество элементов.

Бесконечные множества могут быть также созданы путем бесконечного продолжения последовательности элементов. Например, множество всех положительных нечетных чисел или множество всех степеней числа 2.

Бесконечные множества могут иметь различные степени бесконечности. Некоторые множества могут иметь большую мощность, чем другие бесконечные множества. Например, множество всех вещественных чисел имеет большую мощность, чем множество натуральных чисел. Это означает, что существует бесконечное количество вещественных чисел, которое больше, чем бесконечное количество натуральных чисел.

Бесконечные множества играют важную роль в математике и имеют широкие приложения. Они используются в анализе, теории вероятностей, теории множеств, теории чисел и других областях математики для изучения различных свойств и закономерностей.

Видео по теме:

Вопрос-ответ:

Что такое множество?

Множество — это совокупность различных объектов, называемых элементами множества.

Какие свойства имеет множество?

Множество обладает несколькими свойствами: 1) Множество неупорядочено — порядок элементов не имеет значения; 2) В множестве нет повторяющихся элементов; 3) Множество может быть конечным или бесконечным; 4) Множество может быть пустым (не содержащим ни одного элемента).

Какие примеры можно привести для понимания множеств?

Примеры множеств могут быть разными: 1) Множество всех целых чисел; 2) Множество всех четных чисел; 3) Множество всех красных фруктов; 4) Множество всех студентов в университете и т.д.

Какие операции можно выполнять над множествами?

Над множествами можно выполнять различные операции, такие как объединение, пересечение, разность и дополнение. Операция объединения позволяет получить множество, содержащее все элементы из двух или более множеств. Операция пересечения позволяет получить множество, содержащее только общие элементы из двух или более множеств. Операция разности позволяет получить множество, содержащее элементы, присутствующие в одном множестве, но отсутствующие в другом. Операция дополнения позволяет получить множество, содержащее все элементы, отсутствующие в исходном множестве.

Какова роль множеств в математике?

Множества играют важную роль в математике, так как они являются основой для построения других математических конструкций и теорий. Множества используются для описания и классификации объектов, для решения задач и доказательства теорем. Они также позволяют формализовать различные математические понятия и операции.

Множества чисел

В математике существует несколько типов множеств чисел, каждое из которых имеет свои особенности и свойства. Рассмотрим некоторые из них:

1. Натуральные числа — это множество всех положительных целых чисел, начиная с единицы: 1, 2, 3, 4, 5, и так далее.

2. Целые числа — это множество чисел, включающее все натуральные числа, их противоположности (отрицательные числа) и ноль: …, -3, -2, -1, 0, 1, 2, 3, …

3. Рациональные числа — это множество чисел, представимых в виде дробей, где числитель и знаменатель являются целыми числами и знаменатель не равен нулю. Например, 1/2, -3/4, 0.

4. Иррациональные числа — это множество чисел, которые не могут быть представлены в виде дроби. Примерами иррациональных чисел являются корень из двух (√2), число Пи (π) и число Эйлера (е).

5. Вещественные числа — это множество всех рациональных и иррациональных чисел. Они представляются на числовой прямой и включают в себя все возможные значения.

6. Комплексные числа — это множество чисел, представляемых в виде суммы действительной и мнимой части. Они записываются в виде a + bi, где a и b — действительные числа, а i — мнимая единица.

Это лишь некоторые из типов множеств чисел, которые используются в математике. Каждый из этих типов имеет свои особенности и применения в разных областях науки и повседневной жизни.

Практическое применение множеств в математике

1. Теория вероятностей: Множества используются для описания событий и исследования их вероятности. Например, можно представить множество всех возможных исходов эксперимента и множество событий, которые мы хотим изучить.

2. Теория множеств: Основные понятия и операции над множествами являются основой этой теории. Она занимается изучением свойств множеств и их отношений.

3. Алгебра: Множества используются в алгебре для определения доменов, областей значений и решений уравнений. Множества также могут быть представлены в виде графов и использоваться для анализа их свойств.

4. Комбинаторика: Множества играют важную роль в комбинаторике, где изучаются различные комбинации и перестановки элементов. Множества используются для описания наборов объектов и их сочетаний.

5. Теория графов: В этой области математики множества используются для описания вершин и рёбер графов. Множества могут быть использованы для моделирования и анализа различных сетей и связей между объектами.

Это лишь некоторые примеры практического применения множеств в математике. Они помогают упорядочивать данные, проводить анализ и решать различные задачи, что делает множества важным инструментом для математических исследований и применений в реальном мире.