Что такое полином в математике простыми словами

Полином в математике — это алгебраическое выражение, состоящее из переменных, коэффициентов и операций сложения, вычитания и умножения. Полиномы используются для моделирования и решения различных задач в математике и естественных науках. В данной статье вы узнаете, как определить и классифицировать полиномы, а также как выполнять операции с ними.

Полином – это математическое выражение, состоящее из переменной, называемой переменной полинома, и коэффициентов, которые умножаются на эту переменную и возводятся в степень.

Полиномы могут иметь различные степени, которая определяется самой высокой степенью переменной в полиноме. Коэффициенты могут быть любыми числами, включая рациональные и иррациональные числа.

Например, полином вида 3x^2 + 2x + 1 имеет степень 2, так как переменная x возводится во вторую степень. Коэффициенты этого полинома равны 3, 2 и 1 соответственно.

Полиномы широко используются в математике для описания различных явлений и моделирования. Они позволяют удобно записывать и решать уравнения, а также проводить анализ функций и графиков.

Полином: основные понятия и определения

P(x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0

Здесь P(x) — полином, x — переменная, an, an-1, …, a1, a0 — коэффициенты, а n — степень полинома.

Степень полинома — это наивысшая степень переменной в полиноме. Например, в полиноме P(x) = 3×2 — 2x + 5 степень равна 2.

Коэффициенты полинома могут быть как числами, так и другими полиномами. Например, в полиноме P(x) = 2×3 + (x2 — 3x + 1) коэффициентом для степени 3 будет число 2, а для степени 2 — полином x2 — 3x + 1.

Полиномы могут быть разных видов: многочлены, биномы, триномы и другие. Многочлен — это полином, в котором есть несколько слагаемых. Бином — это полином, состоящий из двух слагаемых. Трином — это полином, состоящий из трех слагаемых. Например, полином P(x) = 4×3 — 2×2 + 3x — 5 является многочленом, а полином P(x) = x2 + 2x — биномом.

Полиномы играют важную роль в математике и используются для решения различных задач, таких как нахождение корней уравнений, интерполяция и аппроксимация функций, анализ данных и др. Они являются основой алгебры и имеют множество свойств и операций, которые позволяют выполнять различные манипуляции с ними.

В заключение, полином — это математическое выражение, состоящее из переменной и коэффициентов, умноженных друг на друга и сложенных между собой. Он имеет степень, которая определяется наивысшей степенью переменной в полиноме. Полиномы имеют разные виды, такие как многочлены, биномы, триномы, и играют важную роль в математике, используясь для решения различных задач и анализа данных.

Что такое полином в математике?

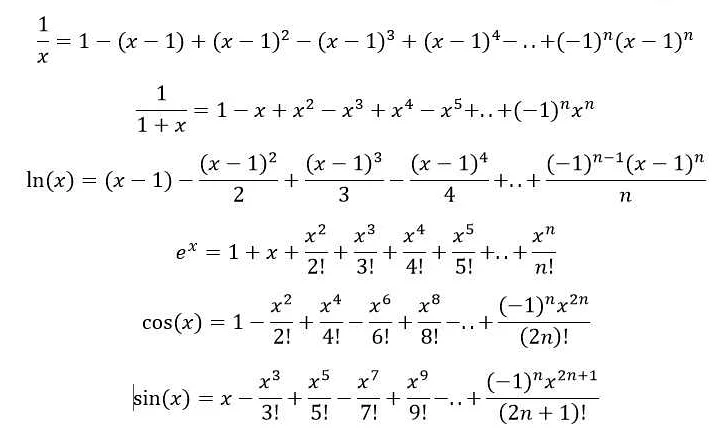
Основной вид полинома представляет собой сумму слагаемых, каждое из которых представляет собой произведение переменной на возведенную в целую степень. Например, полином может иметь вид:

• 3×2 + 2x + 1
• 5×3 — 2×2 + 7x — 3
• 2×4 + 3×3 — x2 + 5x + 4

В полиноме переменная (в данном случае x) может принимать различные значения, а коэффициенты (в данном случае числа) определяют вклад каждого слагаемого в общую сумму.

Полиномы широко используются в математике для описания и анализа различных процессов и явлений, например, при решении уравнений, интерполяции данных, аппроксимации функций и т.д.

Степень полинома и его коэффициенты

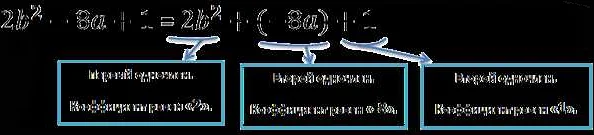
P(x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0

Где P(x) — полином, an, an-1, …, a2, a1, a0 — коэффициенты полинома, x — переменная, а n — степень полинома.

Коэффициенты полинома представляют собой числа, которые умножаются на соответствующие степени переменной. Например, в полиноме P(x) = 3×2 — 2x + 1 коэффициенты равны 3, -2 и 1.

Степень полинома определяет количество слагаемых в полиноме. Например, полином степени 2 содержит 3 слагаемых, полином степени 3 — 4 слагаемых и так далее.

Знание степени полинома и его коэффициентов позволяет анализировать и решать уравнения, проводить графическое изображение полинома и выполнять другие математические операции связанные с полиномами.

Многочлены и их свойства

У многочленов есть несколько важных свойств:

1. Степень многочлена определяется самой большой степенью переменной. В примере выше степень многочлена равна 2.

2. Коэффициенты многочлена могут быть как положительными, так и отрицательными числами. В выражении 3x^2 + 2x — 5 коэффициенты равны 3, 2 и -5 соответственно.

3. Многочлен может иметь свободный член, то есть член без переменной. В примере выше свободным членом является -5.

4. Суммой многочленов является выражение, полученное при сложении коэффициентов и переменных. Например, сумма многочленов 3x^2 + 2x — 5 и 2x^2 + 4x + 1 равна 5x^2 + 6x — 4.

5. Произведением многочленов является выражение, полученное при умножении коэффициентов и переменных. Например, произведение многочленов (3x^2 + 2x — 5) и (2x^2 + 4x + 1) равно 6x^4 + 14x^3 — 11x^2 — 16x — 5.

Многочлены широко используются в математике для решения уравнений, аппроксимации функций и моделирования явлений. Понимание основных свойств многочленов позволяет упростить вычисления и анализировать математические задачи.

Корни полинома и их значения

Значения корней полинома позволяют нам решать уравнения и находить точки пересечения с осями координат. Они имеют важное значение в алгебре и применяются в различных областях, таких как физика, экономика и инженерия.

Корни полинома могут быть как вещественными числами, так и комплексными. Вещественные корни полинома представляют собой значения переменной, которые являются действительными числами. Комплексные корни полинома представляют собой значения переменной, которые являются комплексными числами.

Значение корней полинома позволяет нам понять его поведение и характеристики, такие как количество пересечений с осью абсцисс, экстремумы и точки перегиба.

Важно отметить, что корни полинома могут повторяться, то есть иметь кратность больше 1. Кратность корня определяет, сколько раз он встречается в многочлене. Например, если у полинома есть корень a кратности 2, то он делится на (x — a)^2 без остатка.

Линейные и квадратичные полиномы

В математике полиномом называется алгебраическое выражение, состоящее из одночленов, которые объединены операциями сложения и вычитания. Одночлены, в свою очередь, представляют собой произведение числового коэффициента и переменных, возведенных в натуральные степени.

Линейный полином — это полином первой степени, то есть полином, у которого все одночлены имеют степень равную 1. Он имеет следующий вид: P(x) = a*x + b, где a и b — коэффициенты, x — переменная. Примером линейного полинома может служить выражение P(x) = 3x + 2.

Квадратичный полином — это полином второй степени. Он имеет следующий вид: P(x) = a*x^2 + b*x + c, где a, b и c — коэффициенты, x — переменная. Примером квадратичного полинома может служить выражение P(x) = 2x^2 + 3x + 1.

Линейные и квадратичные полиномы являются основными типами полиномов, которые широко используются в математике и других областях. Они позволяют описывать и моделировать различные явления и процессы, такие как движение, изменение величин и т.д.

Для работы с полиномами существуют различные методы и операции, такие как сложение, вычитание, умножение, деление и нахождение корней. Изучение полиномов и их свойств является важной частью алгебры и математического анализа.

Вид полиномаПримерОбщий вид

Линейный полином	P(x) = 3x + 2	P(x) = a*x + b
Квадратичный полином	P(x) = 2x^2 + 3x + 1	P(x) = a*x^2 + b*x + c

Сложение, вычитание и умножение полиномов

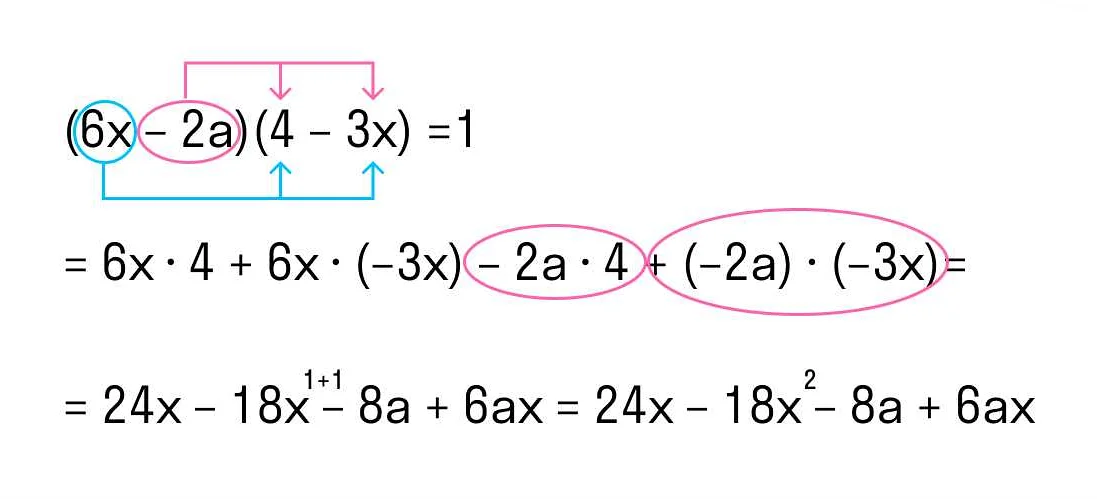
Вычитание полиномов работает аналогично сложению. Мы просто вычитаем коэффициенты одночленов с одинаковыми степенями. Например, если у нас есть полиномы P(x) = 3x^2 + 2x + 1 и Q(x) = 2x^2 + 3x — 5, то результатом их вычитания будет полином R(x) = (3 — 2)x^2 + (2 — 3)x + (1 + 5).

Умножение полиномов происходит путем умножения каждого одночлена одного полинома на каждый одночлен другого полинома, а затем суммирования всех полученных произведений. Например, если у нас есть полиномы P(x) = 3x + 2 и Q(x) = 2x — 1, то результатом их умножения будет полином R(x) = (3x )(2x) + (3x)(-1) + (2)(2x) + (2)(-1), который затем упрощается до R(x) = 6x^2 — 3x + 4x — 2, и, наконец, до R(x) = 6x^2 + x — 2.

Деление полиномов и остаток

При делении одного полинома на другой полином получается частное и остаток. Деление полиномов аналогично делению чисел, только вместо цифр используются переменные и степени.

Чтобы разделить один полином на другой, нужно подобрать такой полином, чтобы при умножении его на делитель получить делимое. Этот полином называется частным. Остаток от деления будет равен разности делимого и произведения частного на делитель.

Деление полиномов может быть представлено в виде алгоритма:

1. Расположить полиномы друг под другом, приведя к одинаковому порядку степеней переменных.
2. Поделить первый член делимого на первый член делителя.
3. Умножить полученное частное на делитель и записать результат под делимым.
4. Вычесть полученное произведение из делимого.
5. Полученную разность снова поделить на первый член делителя.
6. Повторять шаги 3-5 до тех пор, пока степень остатка не будет меньше степени делителя.

Остаток от деления будет состоять из полиномов, у которых степень переменной меньше степени делителя.

Деление полиномов и нахождение остатка от деления являются важными операциями в алгебре и находят применение в различных математических и инженерных задачах.

Вопрос-ответ:

Что такое полином?

Полином — это алгебраическое выражение, состоящее из набора переменных и констант, связанных между собой операциями сложения и умножения.

Какие операции можно выполнять с полиномами?

С полиномами можно выполнять операции сложения, вычитания и умножения. Также можно производить деление полиномов, но в этом случае результат может быть не полиномом, а рациональной дробью.

Какие есть виды полиномов?

Полиномы могут быть одночленами, биномами, триномами и т.д., в зависимости от количества слагаемых. Также они могут быть классифицированы по степени, которая определяется как наибольший показатель степени переменной в полиноме.

Как можно упростить полином?

Для упрощения полинома можно выполнить операции с подобными слагаемыми, то есть сложить или вычесть их. Также можно применить правила раскрытия скобок и сокращения подобных членов. В результате получится более простой вид полинома.

Зачем нужны полиномы в математике?

Полиномы широко применяются в математике и ее приложениях. Они используются для моделирования различных явлений, описания функций и решения уравнений. Также полиномы играют важную роль в алгебре, математическом анализе и других областях математики.

Что такое полином?

Полином — это алгебраическое выражение, состоящее из суммы или разности различных слагаемых, умноженных на степени переменной.

Применение полиномов в реальной жизни

Полиномы, как математический инструмент, находят свое применение во множестве областей реальной жизни. Их использование позволяет моделировать и анализировать различные явления, предсказывать и прогнозировать результаты и делать выводы на основе полученных данных.

Одной из областей, где полиномы применяются, является экономика. В экономической науке полиномы используются для моделирования и анализа экономических процессов, таких как рост экономического индекса, инфляция, спрос и предложение на рынке и т.д. С помощью полиномов можно предсказывать эти процессы, проводить исследования и принимать решения на основе полученных данных.

Еще одной областью, где полиномы находят применение, является физика. В физике полиномы используются для моделирования и анализа различных физических явлений, таких как движение тела, колебания, электромагнитные поля и другие. С помощью полиномов физики могут предсказывать поведение систем и проводить различные эксперименты для подтверждения своих теорий.

Также полиномы находят применение в компьютерной графике и анимации. Они используются для создания плавных и реалистичных движений объектов и персонажей. Математические модели на основе полиномов позволяют создавать различные эффекты и визуальные иллюзии.

Полиномы также используются в статистике и машинном обучении для анализа данных и построения моделей. С их помощью можно проводить регрессионный анализ, прогнозировать тренды и паттерны, а также делать выводы на основе полученных результатов.

Применение полиномов в реальной жизни не ограничено только этими областями. Они используются во множестве других наук и отраслей, таких как биология, химия, финансы, медицина и многое другое. Благодаря своей универсальности и гибкости, полиномы являются мощным инструментом для анализа и моделирования различных явлений в реальной жизни.

Видео по теме: