Что такое степень в математике 5 класс определение

Степень числа в математике 5 класс — это способ записи числа в виде произведения множителей, когда один и тот же множитель умножается на себя определенное количество раз. Узнайте определение и свойства степени числа в 5 классе математики.

Степень — одно из важнейших понятий в математике, которое изучается в 5 классе. Оно используется для работы с числами и позволяет упростить вычисления и запись больших или маленьких чисел.

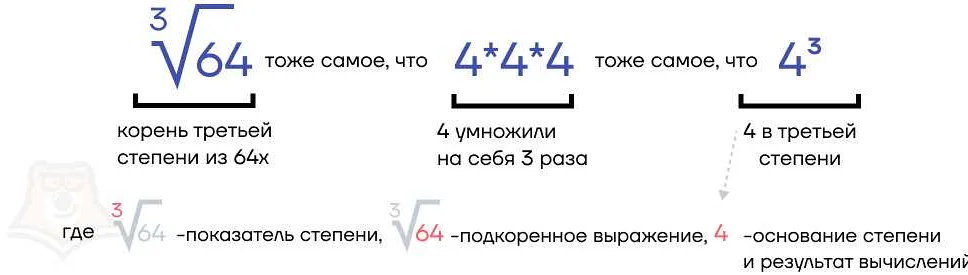
Степень состоит из двух частей: основания и показателя степени. Основание — это число, которое возводится в степень, а показатель степени — это число, указывающее, сколько раз нужно умножить основание на себя. Например, в степени 3 число 2 — это основание, а число 3 — это показатель степени.

При записи степеней используется специальный символ — знак умножения «^». Например, 2^3 означает 2 в степени 3, что равно 2 * 2 * 2 = 8.

Степени могут быть положительными и отрицательными. Если показатель степени положительный, то это означает, что нужно умножить основание на себя столько раз, сколько указано в показателе. Если показатель степени отрицательный, то основание возводится в обратную степень, то есть степень с отрицательным показателем равна 1, делённая на степень с положительным показателем. Например, 2^(-3) равно 1 / (2^3) = 1 / 8 = 0.125.

Определение понятия «степень»

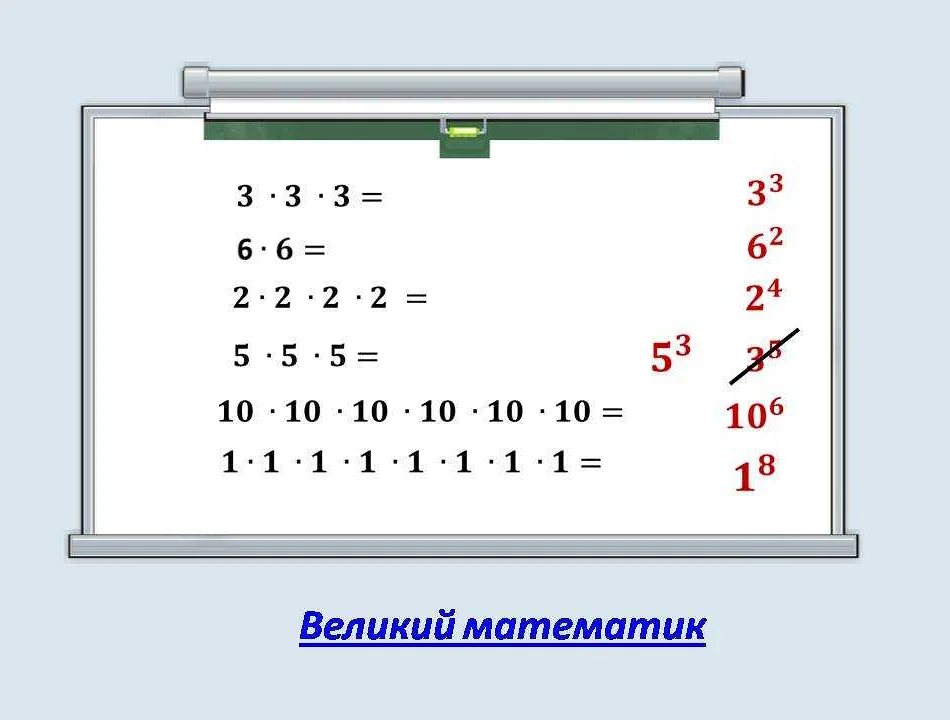
Степень обозначается с помощью символа «^». Например, если нужно возвести число 2 в степень 3, запись будет выглядеть как 2^3. Это означает, что необходимо умножить число 2 на само себя три раза: 2 * 2 * 2 = 8.

Основные понятия, связанные со степенью:

• Положительная степень – когда показатель степени больше нуля.
• Отрицательная степень – когда показатель степени меньше нуля.
• Нулевая степень – когда показатель степени равен нулю. В этом случае любое число, кроме нуля, возводится в нулевую степень и равно 1.

Степень может быть любым целым числом, включая положительные и отрицательные значения.

Видео по теме:

Основные свойства степени

Основные свойства степени включают:

1. Свойство умножения степеней с одинаковым основанием: при умножении степеней с одинаковым основанием и разными показателями, показатели складываются. Например, a^m * a^n = a^(m + n).
2. Свойство деления степеней с одинаковым основанием: при делении степеней с одинаковым основанием и разными показателями, показатели вычитаются. Например, a^m / a^n = a^(m — n).
3. Свойство возведения степени в степень: при возведении степени в степень показатели умножаются. Например, (a^m)^n = a^(m * n).
4. Свойство степени с отрицательным показателем: при возведении в степень с отрицательным показателем, число переворачивается и меняется местами с 1. Например, a^(-n) = 1 / a^n.
5. Свойство степени с нулевым показателем: любое число, кроме 0, возводится в степень 0, равную 1. Например, a^0 = 1.

Понимание и применение этих основных свойств степени поможет в решении различных задач и упростит работу с числами, записанными в степенной форме.

Определение и примеры положительной степени

Положительная степень — это степень, в которой число умножается само на себя заданное количество раз. Например, число 2 в положительной степени 3 будет выглядеть так: 2^3 = 2 * 2 * 2 = 8.

Вот еще несколько примеров положительной степени:

1. Число 5 в степени 2: 5^2 = 5 * 5 = 25.
2. Число 3 в степени 4: 3^4 = 3 * 3 * 3 * 3 = 81.
3. Число 10 в степени 3: 10^3 = 10 * 10 * 10 = 1000.

В положительной степени число всегда умножается само на себя заданное количество раз, что позволяет получить новое число, которое больше исходного в несколько раз.

Вопрос-ответ:

Как определить степень числа?

Степень числа — это число, которое показывает, сколько раз нужно умножить данное число на себя. Например, степень числа 2 равна 4, потому что 2 * 2 = 4. Для определения степени числа нужно записать число в умножаемом виде и указать, сколько раз нужно умножить это число на себя.

Как обозначается степень числа?

Степень числа обозначается с помощью верхнего индекса, который записывается справа от числа. Например, степень числа 2 обозначается как 2 в степени 3 и записывается как 2^3.

Какая степень числа определяет квадрат числа?

Квадрат числа определяется степенью 2. Например, число 4 в квадрате равно 4^2 = 16. То есть, чтобы получить квадрат числа, нужно это число умножить на само себя.

Что такое нулевая степень числа?

Нулевая степень числа всегда равна 1. Например, 5^0 = 1. Все числа, возведенные в нулевую степень, равны 1.

Что такое отрицательная степень числа?

Отрицательная степень числа обозначает, что число находится в знаменателе дроби. Например, число 2 в степени -3 обозначается как 2^-3 и равно 1/2^3 = 1/8. В отрицательной степени число переводится в знаменатель и записывается с положительным показателем степени.

Что такое степень в математике?

Степень в математике — это операция, позволяющая возводить число в некоторую степень, то есть умножать его само на себя определенное количество раз.

Как записывается степень?

Степень записывается с помощью числа, которое называется основанием, и числа, которое называется показателем степени. Основание записывается внизу, а показатель степени — наверху, после знака «^». Например, 2^3 означает, что число 2 возводится в степень 3.

Определение и примеры отрицательной степени

Формально, отрицательная степень числа a обозначается как a-n, где a – число, n – отрицательное целое число.

Примеры отрицательной степени:

• 2-2 = 1/(22) = 1/4
• 3-3 = 1/(33) = 1/27
• 5-1 = 1/(51) = 1/5

Отрицательная степень числа позволяет нам работать с дробными значениями и вычислять их на основе их обратных значений. Она играет важную роль в математике и науке и используется в различных областях, включая физику, экономику и программирование.

Свойства положительной степени

Основные свойства положительной степени:

1. Умножение чисел в степени. Если числа, возведенные в степени, имеют одну и ту же основу, то их степени можно сложить. Например, am * an = am+n.
2. Умножение степени на степень. Если число возводится в степень, а результат возводится в новую степень, то степени можно перемножить. Например, (am)n = am*n.
3. Умножение числа в степени на произведение чисел. Если число возводится в степень, а затем производится операция умножения с другими числами, то можно распределить степень на каждый множитель. Например, am * bm = (a * b)m.
4. Возведение в степень 0. Любое число, кроме 0, возводится в степень 0 равно 1. Например, a0 = 1.
5. Возведение в степень 1. Любое число, включая 0, возводится в степень 1 равно самому числу. Например, a1 = a.

Эти свойства позволяют упростить вычисления и решение задач, связанных со степенями чисел.

Свойства отрицательной степени

Основные свойства отрицательной степени:

1. Свойство переворота: Если число возвести в отрицательную степень, то результат будет обратным значением этого числа в положительной степени. Например, 2^-2 = 1/2^2 = 1/4.

2. Свойство умножения: Число, возведенное в сумму отрицательных степеней, равно произведению чисел, каждое из которых возведено в соответствующую степень. Например, 2^-2 * 2^-3 = 1/2^2 * 1/2^3 = 1/4 * 1/8 = 1/32.

3. Свойство деления: Частное двух чисел, возведенных в отрицательные степени, равно произведению чисел, каждое из которых возведено в соответствующую положительную степень. Например, (2^-2) / (2^-3) = (1/2^2) / (1/2^3) = (1/4) / (1/8) = (1/4) * (8/1) = 8/4 = 2.

4. Свойство степени степени: Число, возведенное в отрицательную степень, а затем в положительную степень, равно числу, возведенному в произведение этих степеней. Например, (2^-2)^3 = (1/2^2)^3 = (1/4)^3 = 1/64.

Знание и применение свойств отрицательной степени позволяет более удобно работать с математическими выражениями и решать задачи, связанные с экспоненциальными функциями.

Определение и примеры нулевой степени

Например:

• 00 = 1
• 10 = 1
• 20 = 1
• 30 = 1

Во всех примерах выше, числа возводятся в нулевую степень, и результатом является число 1. Это свойство нулевой степени применяется во многих математических выражениях и формулах.

Свойства нулевой степени

Степень нуля обладает несколькими особыми свойствами:

1. Любое число, возведенное в степень 0, равно 1. Независимо от значения числа, при возведении его в нулевую степень, результат всегда будет равен 1. Например, 20 = 1, (-3)0 = 1.
2. Нуль в нулевой степени не определен. В математике установлено, что 00 не имеет определенного значения. Разные математические области и задачи могут интерпретировать это выражение по-разному, поэтому ответ на вопрос о значении 00 может быть разным в различных контекстах.
3. Степень нуля в отрицательной степени не определена. Аналогично нулю в нулевой степени, выражение 0-n не имеет определенного значения, где n — отрицательное число. В данном случае, вычисление невозможно, и ответ является неопределенным.

Знание этих свойств поможет вам понять особенности работы со степенями, включая нулевую степень, в математике.