Полином что это в математике

Полином — это математическое выражение, состоящее из переменной и коэффициентов, связанных через операции сложения, вычитания и умножения. Полиномы широко применяются в алгебре и анализе для моделирования и решения различных задач. В этой статье вы узнаете, что такое полином, какие его основные свойства и примеры использования в математике.

Полином — это алгебраическая функция, состоящая из суммы или разности произведений переменных, возведенных в натуральные степени. Они являются одной из основных тем в алгебре и широко используются в различных областях математики, физики, экономики и компьютерных наук.

Определение полинома включает в себя несколько ключевых элементов. Во-первых, полином состоит из переменных, называемых переменными полинома. Эти переменные могут принимать любые значения и обычно обозначаются буквами. Второй элемент — это коэффициенты, которые умножаются на каждую переменную в полиноме. Коэффициенты могут быть любыми числами, включая целые числа, рациональные числа и действительные числа. И, наконец, полином имеет степень, которая определяется наивысшей степенью переменной в полиноме.

Пример полинома: 3x^2 + 2xy — 5

В данном примере полином состоит из трех термов. Первый терм 3x^2 состоит из переменной x, возведенной в степень 2, и коэффициента 3. Второй терм 2xy состоит из двух переменных x и y и коэффициента 2. И третий терм -5 состоит только из коэффициента -5.

Полиномы играют важную роль в алгебре и имеют множество применений. Они используются для моделирования реальных процессов, решения уравнений, аппроксимации функций и многое другое. Понимание полиномов позволяет математикам и ученым анализировать и предсказывать различные явления и является фундаментальной частью математической грамотности.

Определение полинома в математике

Полиномы могут содержать одну или несколько переменных, обозначаемых буквами, например, x, y, z. Коэффициенты могут быть любыми числами, включая целые числа, дроби и даже комплексные числа.

Степень полинома — это наивысшая степень переменной в полиноме. Например, в полиноме 2x^3 + 3x^2 — 5x + 1 степень полинома равна 3, так как наивысшая степень переменной x равна 3.

Примеры полиномов:

2x^3 + 3x^2 — 5x + 1

4x^2y^3 — 2xy + 7

6a^2b — 9ab^2 + 12ab

Полиномы широко используются в математике для решения уравнений, моделирования функций и анализа данных.

Видео по теме:

Структура полинома

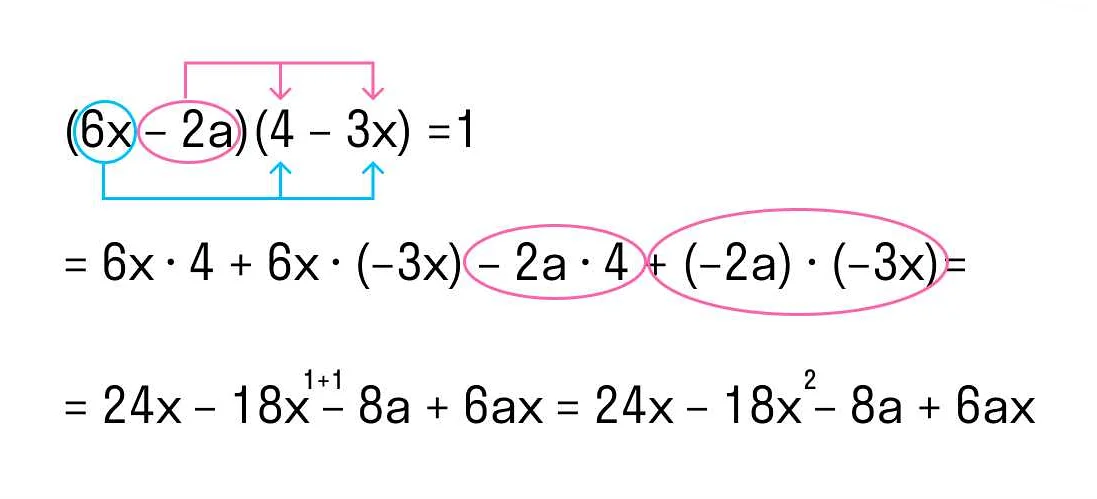
Структура полинома представляет собой сумму или разность одночленов, где каждый одночлен состоит из коэффициента и переменной, возведенной в степень.

Например, полином может иметь следующую структуру:

• 2×3 — 5×2 + 3x — 7
• 4y2 + 2
• 3a4 — 2b3 + 5c2 — d

В приведенных примерах полиномы состоят из одночленов, в которых переменные возводятся в неотрицательные целые степени (3, 2, 1, 0, и так далее). Коэффициенты (2, -5, 3, -7 и т. д.) представляют числа, умноженные на переменные.

Степень полинома и его коэффициенты

Степень полинома определяется наибольшим показателем переменной в его мономах. Например, если полином имеет вид:

$$P(x) = a_nx^n + a_{n-1}x^{n-1} + \ldots + a_1x + a_0$$

где $$a_n, a_{n-1}, \ldots, a_1, a_0$$ — коэффициенты полинома, а $$n$$ — его степень, то степень полинома равна $$n$$.

Коэффициенты полинома могут быть как числами, так и переменными. Числовые коэффициенты обычно обозначаются буквами $$a, b, c, \ldots$$, а переменные коэффициенты — буквами $$p, q, r, \ldots$$

Например, полином $$P(x) = 2x^3 — 3x^2 + 4x — 1$$ имеет степень 3 и коэффициенты $$2, -3, 4, -1$$.

Степень полинома позволяет определить его свойства, такие как количество корней и поведение графика полинома.

Операции с полиномами

В математике существуют несколько основных операций, которые можно выполнять с полиномами.

Сложение и вычитание полиномов:

• Для сложения полиномов их соответствующие слагаемые с одинаковыми степенями складываются или вычитаются. Например, чтобы сложить полиномы 3x^2 + 2x + 1 и 5x^2 — 4x + 2, необходимо сложить коэффициенты при одинаковых степенях:
  • 3x^2 + 5x^2 = 8x^2
  • 2x — 4x = -2x
  • 1 + 2 = 3

  Получаем полином 8x^2 — 2x + 3.

Умножение полиномов:

• Для умножения полиномов необходимо каждое слагаемое первого полинома умножить на каждое слагаемое второго полинома, а затем сложить полученные произведения. Например, чтобы умножить полиномы (2x + 3) и (4x — 1), выполним следующие действия:
  • 2x * 4x = 8x^2
  • 2x * (-1) = -2x
  • 3 * 4x = 12x
  • 3 * (-1) = -3

  Затем сложим полученные произведения: 8x^2 — 2x + 12x — 3. Получаем полином 8x^2 + 10x — 3.

Деление полиномов:

• Деление полиномов — это процесс нахождения частного и остатка от деления одного полинома на другой. Деление полиномов осуществляется по аналогии с делением чисел, где степени полиномов служат вместо цифр. Результатом деления будет частное и остаток. Например, при делении полинома 3x^2 + 2x + 1 на полином x — 1 получим:
  • Частное: 3
  • Остаток: 5x + 6

  Получаем результат деления: 3 с остатком 5x + 6.

Возведение полинома в степень:

• Возведение полинома в целую положительную степень выполняется путем многократного умножения полинома самого на себя. Например, чтобы возвести полином 2x + 1 в квадрат, нужно выполнить следующие действия:
  • (2x + 1) * (2x + 1) = 4x^2 + 2x + 2x + 1
  • Упрощаем: 4x^2 + 4x + 1

  Получаем полином 4x^2 + 4x + 1.

Примеры полиномов

В математике полиномом называется алгебраическое выражение, состоящее из переменных и констант, а также операций сложения, вычитания и умножения. Вот несколько примеров полиномов:

Пример 1:

3x^2 + 5x — 2

Это полином второй степени, так как самая высокая степень переменной x равна 2.

Пример 2:

4y^3 — 2y^2 + 7y + 1

Это полином третьей степени, так как самая высокая степень переменной y равна 3.

Пример 3:

2a^4 — 3a^2 + 4a — 1

Это полином четвертой степени, так как самая высокая степень переменной a равна 4.

Пример 4:

8x^5 + 2x^3 — 6x

Это полином пятой степени, так как самая высокая степень переменной x равна 5.

Таким образом, полиномы могут иметь различную степень, включая нулевую степень (когда полином равен константе).

Основные свойства полиномов

Полиномы в математике обладают рядом особенностей, которые позволяют нам анализировать их свойства и использовать их в различных приложениях. Ниже приведены основные свойства полиномов:

• Степень полинома: степень полинома определяется как наивысшая степень переменной в полиноме. Например, полином вида 3x^2 + 2x + 1 имеет степень 2.
• Коэффициенты полинома: коэффициенты полинома — это числа, которые умножаются на каждую переменную в полиноме. Например, в полиноме 3x^2 + 2x + 1 коэффициенты равны 3, 2 и 1.
• Термы полинома: термы полинома — это отдельные выражения, состоящие из коэффициента и переменной, возведенной в степень. Например, в полиноме 3x^2 + 2x + 1 есть три терма: 3x^2, 2x и 1.
• Старший коэффициент: старший коэффициент полинома — это коэффициент, умножаемый на переменную с наивысшей степенью. В полиноме 3x^2 + 2x + 1 старший коэффициент равен 3.
• Многочлены одинаковой степени: многочлены одинаковой степени сравниваются путем сравнения их старших коэффициентов. Многочлен с более высоким старшим коэффициентом считается более важным.

Это основные свойства полиномов, которые помогают в их анализе и использовании в различных областях математики и ее приложениях.

Применение полиномов в математике и физике

Полиномы широко применяются в математике и физике для моделирования различных явлений и решения задач. Вот некоторые области, где полиномы находят свое применение:

1. Алгебраическая геометрия: полиномы используются для изучения геометрических объектов, таких как алгебраические кривые и поверхности.
2. Математический анализ: полиномы используются для приближения сложных функций и вычисления интегралов.
3. Теория вероятностей: полиномы Лежандра и полиномы Чебышева используются для аппроксимации распределений и оценки вероятностей.
4. Теория чисел: полиномы используются для изучения простых чисел и факторизации чисел.
5. Физика: полиномы используются для моделирования движения тел, электромагнитных полей, колебаний и волн.

Во всех этих областях полиномы позволяют описывать и анализировать сложные математические и физические явления, что делает их важным инструментом в научных и инженерных расчетах.

Вопрос-ответ:

Что такое полином?

Полином — это выражение, состоящее из переменных и констант, связанных только с операциями сложения, вычитания и умножения. Он может быть записан в виде многочлена, в котором переменные возводятся в натуральные степени.

Какие операции можно выполнять с полиномами?

С полиномами можно выполнять операции сложения, вычитания и умножения. Также можно находить значения полинома при заданных значениях переменных и находить корни полинома.

Как записывается полином в математике?

Полином обычно записывается в виде многочлена, где переменные возводятся в натуральные степени, а коэффициенты при этих степенях могут быть как числами, так и другими переменными или выражениями. Например, полином 3x^2 + 2xy — 5z^3.

Какие есть примеры полиномов?

Примерами полиномов могут быть: 2x^3 + 5x^2 — 7x + 3, a^2b^3 — 4ab + 2, 3x^4 + 2x^3 — 5x^2 + x — 1. Все эти выражения являются многочленами, состоящими из переменных, возведенных в степени.

Какие свойства имеют полиномы?

У полиномов есть несколько свойств. Например, сумма или разность двух полиномов также является полиномом. Произведение двух полиномов также является полиномом. Также полином может иметь корни — значения переменных, при которых полином равен нулю.

Что такое полином в математике?

Полином в математике — это алгебраическое выражение, состоящее из переменных и коэффициентов, объединенных операциями сложения и умножения.