Что такое правильная дробь в математике 5 класс

Правильная дробь – это дробь, в которой числитель меньше знаменателя. В математике 5 класса правильные дроби являются основным понятием, их можно сравнивать, складывать, вычитать и умножать. Узнайте подробности о правильных дробях и их использовании в математике 5 класса.

Правильная дробь — это одна из основных форм представления десятичных дробей в математике. В 5 классе, ученики начинают изучать этот вид дробей, который имеет свои особенности и правила записи. Правильная дробь представляет собой число, которое меньше единицы и имеет числитель, меньший знаменателя. В обычной десятичной форме правильная дробь представляется числом с запятой, где цифры после запятой образуют бесконечную последовательность.

Определить правильную дробь можно, сравнивая числитель и знаменатель. Если числитель меньше знаменателя, то дробь является правильной. Например, дробь 3/5 является правильной, так как числитель (3) меньше знаменателя (5). Однако дробь 5/3 не является правильной, так как числитель (5) больше знаменателя (3).

Примеры правильных дробей:

• 1/2 — числитель (1) меньше знаменателя (2)
• 2/3 — числитель (2) меньше знаменателя (3)
• 3/4 — числитель (3) меньше знаменателя (4)

Знание правильных дробей важно для дальнейшего изучения математики, так как они являются основой для работы с десятичными дробями и пропорциями. Правильные дроби широко используются в различных областях науки и повседневной жизни, их понимание поможет ученикам лучше разбираться в математических задачах и ситуациях.

Определение правильной дроби

Например, дроби 1/2, 3/4 и 2/3 являются правильными дробями. Во всех этих случаях числитель (1, 3, 2) меньше знаменателя (2, 4, 3), и эти дроби не могут быть упрощены.

Правильные дроби часто используются для представления части целого числа или долей от целого числа. Например, если у вас есть 3 яблока, а вы съели 2/3, то осталось 1/3 или одно яблоко. В этом случае 1/3 является правильной дробью, представляющей часть от целого числа.

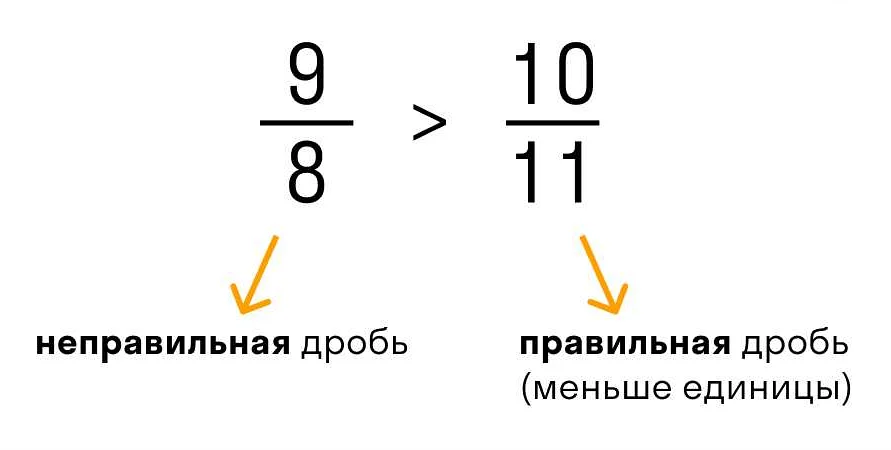
Важно отметить, что правильная дробь отличается от неправильной дроби, у которой числитель больше знаменателя. Например, дроби 5/4, 7/3 и 4/2 являются неправильными дробями, так как числитель больше знаменателя.

Видео по теме:

Примеры правильных дробей

1. 1/2 — одна вторая;
2. 3/4 — три четверти;
3. 2/3 — две трети;
4. 5/8 — пять восьмых;
5. 7/10 — семь десятых;

Это лишь несколько примеров правильных дробей. Все они имеют числитель, который меньше знаменателя и представляют собой часть от целого числа.

Свойства правильных дробей

1. Числитель правильной дроби всегда положительный и меньше знаменателя.
2. Знаменатель правильной дроби всегда положительный и больше числителя.
3. Правильные дроби можно представить в виде смешанной дроби, где целая часть равна нулю.
4. Правильные дроби можно сокращать, то есть уменьшать числитель и знаменатель на одно и то же число.
5. Сумма или разность двух правильных дробей всегда являются правильной дробью.
6. Умножение двух правильных дробей также дает правильную дробь.
7. Деление правильной дроби на целое число или другую правильную дробь также дает правильную дробь.

Наличие этих свойств позволяет упрощать вычисления с правильными дробями и выполнять различные математические операции с ними.

Сравнение правильных дробей

Для того чтобы сравнить две правильные дроби, сначала сравнивают их числители. Если числители равны, то сравнивают знаменатели. Если числители и знаменатели обеих дробей равны, значит, дроби равны.

Если числители и знаменатели разные, необходимо привести дроби к общему знаменателю и сравнить их числители. Дробь с большим числителем будет больше, а дробь с меньшим числителем будет меньше.

Пример:

Сравним дроби 3/5 и 2/5:

Так как знаменатели (5) равны, сравниваем числители. 3 больше, чем 2, поэтому дробь 3/5 больше, чем 2/5.

Сравним дроби 2/3 и 2/4:

Поскольку знаменатели (3 и 4) разные, необходимо привести дроби к общему знаменателю. Общий знаменатель будет равен 12.

2/3 = 8/12, 2/4 = 6/12.

Теперь можно сравнить числители: 8 больше, чем 6. Значит, дробь 2/3 больше, чем 2/4.

Таким образом, сравнение правильных дробей позволяет определить их относительный размер и сравнить их между собой.

Сокращение правильных дробей

Для сокращения правильных дробей нужно найти их наибольший общий делитель (НОД) числителя и знаменателя. НОД — это наибольшее число, на которое можно одновременно поделить числитель и знаменатель.

Например, у нас есть дробь 6/9. Чтобы сократить ее, мы найдем НОД числителя 6 и знаменателя 9. НОД(6, 9) равен 3. Делим числитель и знаменатель на 3, получаем сокращенную дробь 2/3.

Сокращение правильных дробей помогает упростить вычисления и работу с дробными числами. Оно также помогает нам видеть эквивалентные дроби и сравнивать их легче.

Например, если у нас есть две дроби: 2/4 и 1/2, то мы знаем, что они равны, потому что они обе сокращены до 1/2.

Поэтому, сокращение правильных дробей является важным навыком в математике 5 класса, который поможет нам лучше понимать и работать с дробными числами.

Сложение и вычитание правильных дробей

Правильные дроби могут быть сложены или вычтены, используя определенные правила. Для сложения и вычитания правильных дробей необходимо следовать следующим шагам:

1. Найти общий знаменатель: При сложении или вычитании правильных дробей необходимо найти общий знаменатель. Общий знаменатель — это число, на которое можно помножить знаменатели обеих дробей, чтобы получить одинаковые знаменатели.

2. Привести дроби к общему знаменателю: После нахождения общего знаменателя необходимо привести обе дроби к этому знаменателю. Для этого необходимо умножить числитель и знаменатель каждой дроби на такое число, чтобы знаменатель стал равным общему знаменателю.

3. Сложить или вычесть числители: После приведения дробей к общему знаменателю можно сложить или вычесть числители. При сложении или вычитании числителей общий знаменатель остается неизменным.

4. Упростить дробь: После сложения или вычитания числителей, если это возможно, необходимо упростить полученную дробь, то есть сократить числитель и знаменатель на их наибольший общий делитель.

Пример:

Дано: $\frac{2}{3}$ + $\frac{1}{4}$

Шаг 1: Общий знаменатель равен 12.

Шаг 2: Приводим дроби к общему знаменателю:

$\frac{2}{3}$ = $\frac{2 \cdot 4}{3 \cdot 4}$ = $\frac{8}{12}$

$\frac{1}{4}$ = $\frac{1 \cdot 3}{4 \cdot 3}$ = $\frac{3}{12}$

Шаг 3: Складываем числители:

$\frac{8}{12}$ + $\frac{3}{12}$ = $\frac{8 + 3}{12}$ = $\frac{11}{12}$

Шаг 4: Упрощаем дробь:

$\frac{11}{12}$ — упрощенная правильная дробь.

Таким образом, результат сложения правильных дробей $\frac{2}{3}$ и $\frac{1}{4}$ равен $\frac{11}{12}$.

Умножение и деление правильных дробей

Правила умножения правильных дробей:

1. Умножаем числитель первой дроби на числитель второй дроби, получаем новый числитель.
2. Умножаем знаменатель первой дроби на знаменатель второй дроби, получаем новый знаменатель.
3. Полученный числитель и знаменатель образуют новую правильную дробь.

Пример:

Дано: 2/3 * 3/4

Решение:

1. Умножаем числитель первой дроби (2) на числитель второй дроби (3), получаем новый числитель (6).
2. Умножаем знаменатель первой дроби (3) на знаменатель второй дроби (4), получаем новый знаменатель (12).
3. Полученная дробь: 6/12.

Правила деления правильных дробей:

1. Умножаем числитель первой дроби на знаменатель второй дроби, получаем новый числитель.
2. Умножаем знаменатель первой дроби на числитель второй дроби, получаем новый знаменатель.
3. Полученный числитель и знаменатель образуют новую правильную дробь.

Пример:

Дано: 2/3 : 4/5

Решение:

1. Умножаем числитель первой дроби (2) на знаменатель второй дроби (5), получаем новый числитель (10).
2. Умножаем знаменатель первой дроби (3) на числитель второй дроби (4), получаем новый знаменатель (12).
3. Полученная дробь: 10/12.

Важно помнить, что полученные дроби можно сократить, то есть убрать общие делители у числителя и знаменателя.

Таким образом, умножение и деление правильных дробей является простым процессом, требующим лишь умения умножать и делить числа.

Задачи на правильные дроби в 5 классе

Одна из задач, которую ученики могут встретить, звучит так: «Разделите круг на 4 равные части, а затем окрасьте 3 из них. Какую дробь показывают окрашенные части?». В данной задаче ученикам нужно понять, что окрашено 3 из 4 равных частей, то есть окрашенная часть составляет $\frac{3}{4}$ от всего круга.

Еще одна задача может звучать так: «Аня выпила $\frac{2}{3}$ стакана воды, а Катя выпила $\frac{5}{6}$ стакана воды. Кто из них выпил больше?». Чтобы решить эту задачу, ученикам нужно сравнить две правильные дроби и сделать вывод, что $\frac{5}{6}$ больше, чем $\frac{2}{3}$.

Также ученики могут сталкиваться с задачами на сложение и вычитание правильных дробей. Например: «Сложите $\frac{2}{5}$ и $\frac{3}{5}$». Чтобы решить эту задачу, ученикам нужно привести обе дроби к общему знаменателю, который в данном случае равен 5, и сложить числители. Ответ будет $\frac{5}{5}$, что равно 1.

Задачи на правильные дроби в 5 классе помогают ученикам углубить свое понимание этой математической концепции и научиться применять ее на практике. Решение таких задач требует логического мышления и навыков работы с дробями.

Вопрос-ответ:

Что такое правильная дробь?

Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, 1/2, 3/4, 2/5 — все они являются правильными дробями.

Какие примеры правильных дробей можно привести?

Примеры правильных дробей: 1/3, 2/5, 3/8, 4/7, 5/9 и так далее. Все эти дроби имеют числитель, который меньше знаменателя.

Чем правильная дробь отличается от неправильной?

Правильная дробь отличается от неправильной тем, что у правильной дроби числитель меньше знаменателя, а у неправильной дроби числитель больше знаменателя. Например, 3/4 — правильная дробь, а 5/3 — неправильная дробь.

Как можно представить правильную дробь в виде смешанного числа?

Правильную дробь можно представить в виде смешанного числа, если ее знаменатель больше числителя. Например, дробь 4/3 можно представить в виде смешанного числа 1 1/3.