Что такое правильные и неправильные дроби в математике

Правильные и неправильные дроби — это основные понятия в математике, которые объясняют различия между числами, состоящими из целой и дробной части. Узнайте, как определить, является ли дробь правильной или неправильной и как они используются в различных математических операциях.

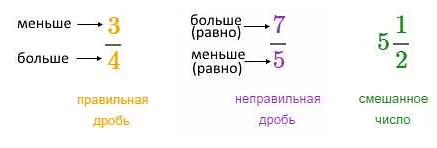
Дробь – это числовая форма представления рационального числа, состоящая из двух числителя и знаменателя, разделенных чертой. В математике существуют два типа дробей: правильные и неправильные. Правильная дробь – это дробь, числитель которой меньше знаменателя. Неправильная дробь – это дробь, числитель которой больше или равен знаменателю.

Важно отметить, что правильные и неправильные дроби могут быть положительными или отрицательными. Положительная дробь имеет положительный знак перед числителем, а отрицательная – отрицательный. Чтобы привести дробь к правильному виду, нужно провести операцию деления числителя на знаменатель. Если результат равен нулю, то дробь является правильной. Если результат больше нуля, то дробь является неправильной.

Примерами правильных дробей являются: 1/2, 3/4, 5/8. Примерами неправильных дробей являются: 3/2, 5/4, 7/6. Важно уметь различать правильные и неправильные дроби, так как это помогает в решении различных задач в математике, например, при работе с дробями в арифметических операциях.

Что такое дробь в математике и какие бывают ее виды

В зависимости от значения числителя и знаменателя, дроби делятся на два основных вида: правильные и неправильные.

Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, дробь 3/4 является правильной, так как 3 меньше 4.

Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, дробь 5/2 является неправильной, так как 5 больше 2.

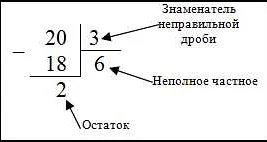
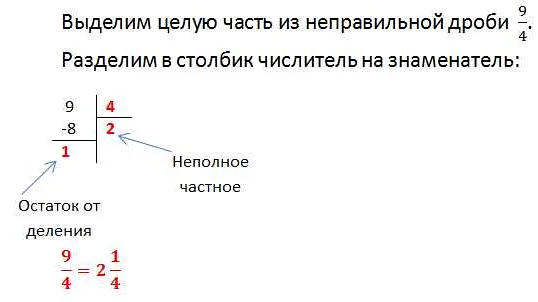
Однако, неправильная дробь можно преобразовать в смешанную дробь, где целая часть и дробная часть записываются отдельно. Например, дробь 5/2 можно записать как смешанную дробь 2 1/2.

Важно отметить, что дроби могут быть положительными или отрицательными, что зависит от знака числителя и знаменателя.

Вывод: Дробь — это числовое представление доли или части целого числа. Она может быть правильной или неправильной в зависимости от значения числителя и знаменателя.

Что такое правильная дробь и как ее определить

Для определения, является ли дробь правильной, нужно сравнить числитель и знаменатель. Если числитель меньше знаменателя, то дробь будет правильной. Например, дроби 1/2, 2/3, 3/4 являются правильными, так как числитель в каждой дроби меньше знаменателя.

Правильные дроби обладают некоторыми характеристиками. Во-первых, их значение всегда меньше единицы, так как числитель меньше знаменателя. Во-вторых, чем больше знаменатель, тем меньше значение дроби. Например, дробь 1/2 меньше дроби 1/3, так как знаменатель во второй дроби больше. В-третьих, правильные дроби можно представить в виде смешанной дроби или десятичной дроби.

Знание о правильных дробях важно при работе с дробями, так как они являются одним из основных типов дробей и используются в различных математических операциях, включая сложение, вычитание, умножение и деление дробей. Правильные дроби также имеют практическое применение в реальной жизни, например, при расчете долей, процентов и вероятностей.

Что такое неправильная дробь и как ее определить

Чтобы определить, является ли дробь правильной или неправильной, нужно сравнить числитель и знаменатель. Если числитель больше знаменателя, то дробь неправильная. Если числитель меньше или равен знаменателю, то дробь правильная.

Неправильные дроби могут быть представлены в виде смешанных чисел или десятичных дробей. Смешанное число состоит из целой части и дробной части. Например, неправильная дробь 5/3 можно записать как смешанное число 1 2/3.

Неправильные дроби могут быть использованы для представления чисел больше единицы. Они широко применяются в различных областях, таких как физика, экономика, архитектура и т.д. Поэтому важно понимать, как определить и работать с неправильными дробями.

Примеры неправильных дробейСмешанные числаДесятичные дроби

3/2	1 1/2	1.5
7/4	1 3/4	1.75
11/5	2 1/5	2.2

Примеры правильных дробей в математике

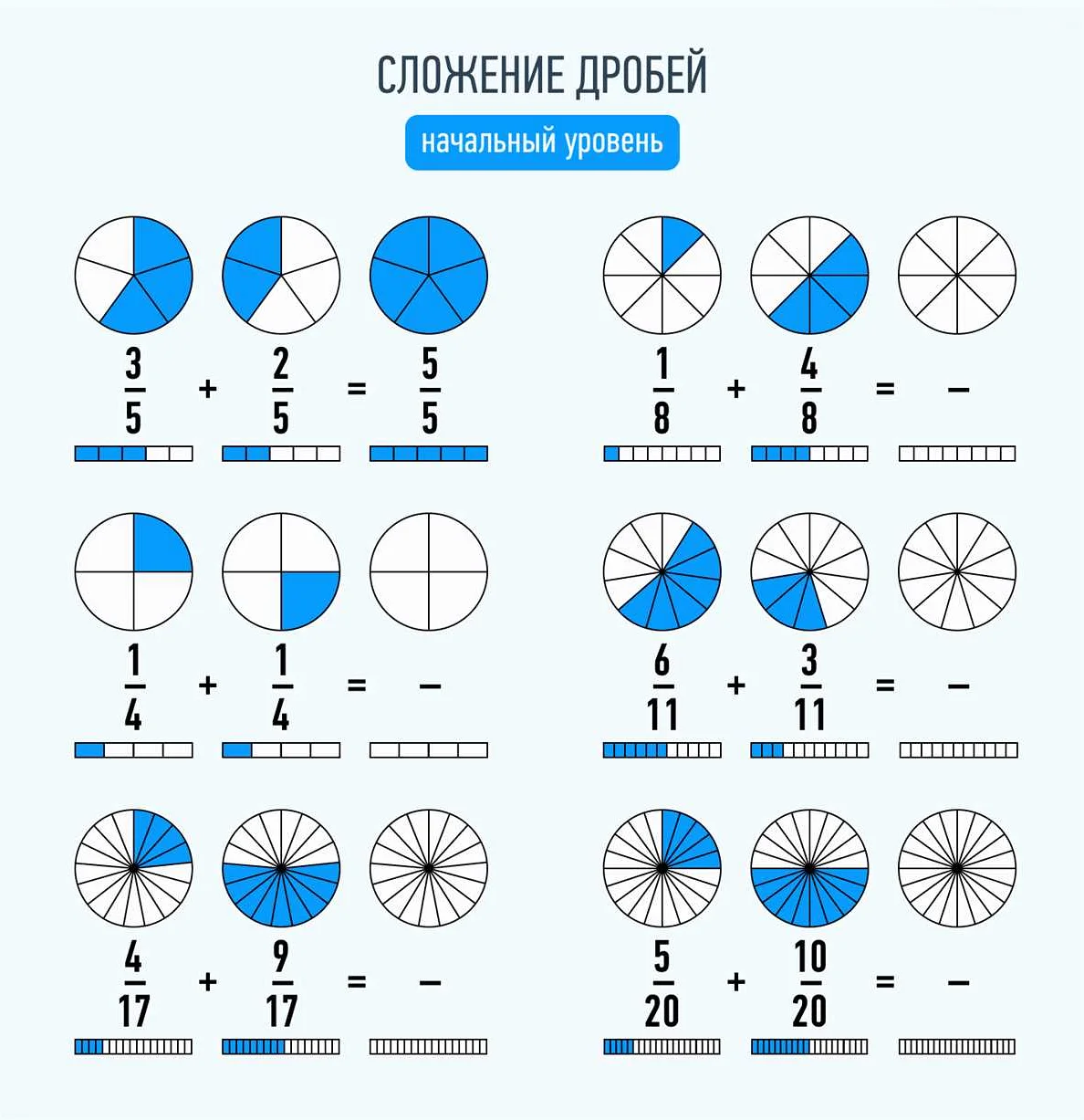
• 1/2 — половина единицы;
• 3/4 — три четверти;
• 7/8 — семь восьмых;
• 2/3 — две трети;
• 5/6 — пять шестых;

Это лишь некоторые из множества примеров правильных дробей. Они широко используются в различных областях математики и других наук, а также в повседневной жизни.

Примеры правильных дробей с числителем 1

1/2	Одна вторая — это пример правильной дроби с числителем 1. Здесь числитель равен 1, а знаменатель равен 2. Эта дробь представляет собой одну половину от целого.
1/3	Одна треть — это еще один пример единичной правильной дроби. Здесь числитель равен 1, а знаменатель равен 3. Эта дробь представляет собой одну треть от целого.
1/4	Одна четвертая — это также пример правильной дроби с числителем 1. Здесь числитель равен 1, а знаменатель равен 4. Эта дробь представляет собой одну четвертую от целого.

Единичные правильные дроби — это особый вид дробей, которые играют важную роль в математике. Они позволяют нам выражать доли от целых чисел и использовать их в различных расчетах и проблемах.

Примеры правильных дробей с числителем больше 1

1. Дробь 2/3. В данном случае числитель равен 2, а знаменатель равен 3. Это пример правильной дроби, потому что 2 меньше 3.
2. Дробь 5/8. В данном случае числитель равен 5, а знаменатель равен 8. Это также пример правильной дроби, так как 5 меньше 8.
3. Дробь 3/5. В данном случае числитель равен 3, а знаменатель равен 5. Это также пример правильной дроби, потому что 3 меньше 5.

Примеры правильных дробей с числителем больше 1 показывают, что дроби могут быть правильными, несмотря на то, что числитель больше знаменателя. Это важно учитывать при работе с дробями в математике.

Примеры неправильных дробей в математике

Вот несколько примеров неправильных дробей:

1. 3/2

В данном примере числитель равен 3, а знаменатель равен 2. Так как 3 больше 2, эта дробь является неправильной.

2. 7/4

В этом примере числитель равен 7, а знаменатель равен 4. Так как 7 больше 4, эта дробь также является неправильной.

3. 11/5

В данном примере числитель равен 11, а знаменатель равен 5. Так как 11 больше 5, эта дробь также является неправильной.

Неправильные дроби играют важную роль в математике и используются при решении различных задач и примеров.

Примеры неправильных дробей с числителем меньше знаменателя

Неправильные дроби представляют собой дроби, у которых числитель больше знаменателя. Однако, также существуют случаи, когда числитель меньше знаменателя, и эти дроби также считаются неправильными.

Ниже приведены несколько примеров неправильных дробей с числителем меньше знаменателя:

1. 1/2 — в этом примере числитель равен 1, а знаменатель равен 2. Числитель меньше знаменателя, поэтому эта дробь является неправильной.

2. 2/3 — в этом примере числитель равен 2, а знаменатель равен 3. Числитель меньше знаменателя, поэтому эта дробь также является неправильной.

3. 3/4 — в этом примере числитель равен 3, а знаменатель равен 4. Числитель меньше знаменателя, поэтому эта дробь также считается неправильной.

4. 4/5 — в этом примере числитель равен 4, а знаменатель равен 5. Числитель меньше знаменателя, поэтому эта дробь является неправильной.

5. 5/6 — в этом примере числитель равен 5, а знаменатель равен 6. Числитель меньше знаменателя, поэтому эта дробь также считается неправильной.

Приведенные выше примеры показывают, что неправильные дроби могут иметь разнообразные значения числителя и знаменателя, но при этом числитель всегда будет меньше знаменателя.

Примеры неправильных дробей с числителем больше знаменателя

1. 7/4

В этом примере числитель равен 7, а знаменатель равен 4. Такая дробь неправильная, потому что числитель больше знаменателя. Ее можно упростить до смешанной дроби или десятичной дроби.

2. 9/5

В данном примере числитель равен 9, а знаменатель равен 5. Эта дробь также является неправильной, так как числитель больше знаменателя. Ее можно представить в виде смешанной дроби или десятичной дроби.

3. 11/6

В этом примере числитель равен 11, а знаменатель равен 6. Эта дробь также является неправильной, так как числитель больше знаменателя. Она может быть записана в виде смешанной дроби или десятичной дроби.

Неправильные дроби с числителем больше знаменателя часто встречаются в математике и могут быть использованы для решения различных задач и проблем. Важно уметь их распознавать и правильно обрабатывать в контексте задачи.

Вопрос-ответ:

Что такое правильные и неправильные дроби в математике?

Правильные дроби — это дроби, у которых числитель меньше знаменателя. Неправильные дроби — это дроби, у которых числитель больше или равен знаменателю.

Можете привести примеры правильных дробей?

Конечно! Примеры правильных дробей: 1/2, 2/3, 3/4 и 4/5. Во всех этих дробях числитель меньше знаменателя.

Какие примеры можно привести неправильных дробей?

Неправильные дроби примеры: 3/2, 5/4, 7/3 и 9/5. Во всех этих дробях числитель больше знаменателя.

Можно ли сократить правильную дробь?

Да, правильные дроби можно сокращать. Например, дробь 4/8 можно сократить до 1/2, так как числитель и знаменатель делятся на 4.

Какие правила относятся к сложению правильных и неправильных дробей?

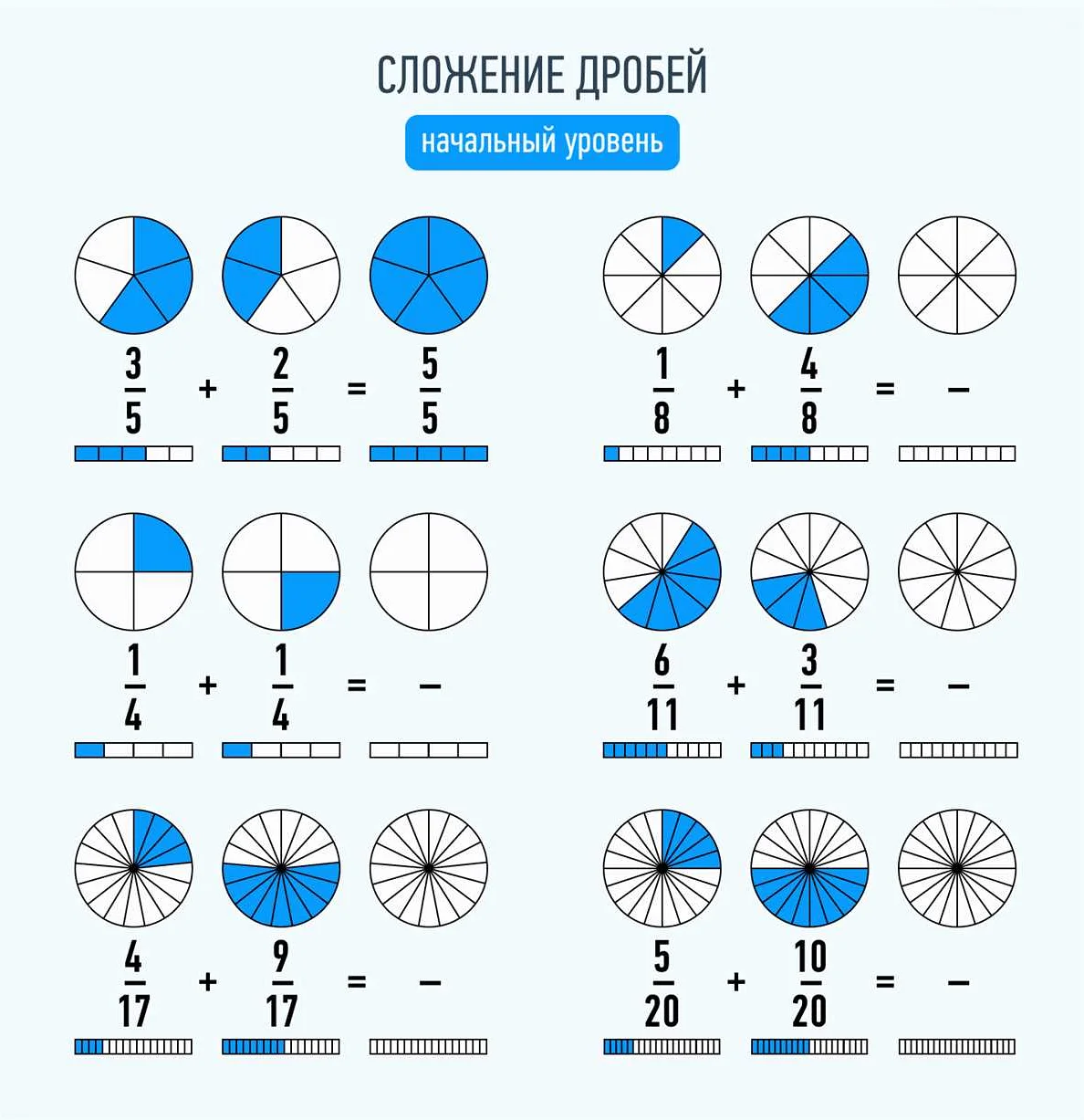
При сложении правильных и неправильных дробей нужно привести их к общему знаменателю и затем сложить числители. Например, 1/2 + 3/4 = 2/4 + 3/4 = 5/4.

Что такое правильные дроби?

Правильные дроби — это дроби, у которых числитель меньше знаменателя. Например, 1/2, 3/4, 5/8 — все они являются правильными дробями.

Видео по теме: