Что такое произведение в математике 2 класс
Содержимое
- 1 Что такое произведение в математике 2 класс
- 1.1 Что такое произведение в математике 2 класс
- 1.2 Определение произведения
- 1.3 Как считать произведение
- 1.4 Примеры вычисления произведения
- 1.5 Свойства произведения
- 1.6 Произведение числа на 0
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.8.0.1 Какое определение произведения в математике во 2 классе?
- 1.8.0.2 Какими способами можно найти произведение?
- 1.8.0.3 Какие особенности имеет произведение в математике 2 класса?
- 1.8.0.4 Какие примеры произведения можно привести для уточнения понятия?
- 1.8.0.5 Какими методами можно учить детей произведение в математике 2 класса?
- 1.8.0.6 Что такое произведение в математике?
- 1.8.0.7 Как вычислить произведение?
- 1.9 Произведение числа на 1
- 1.10 Закрепление материала по произведению
Произведение в математике для учащихся 2 класса — это результат умножения двух чисел. Узнайте, как правильно выполнять умножение и использовать произведение в различных задачах и упражнениях.
Произведение — это одна из основных арифметических операций в математике. Во втором классе ученики начинают изучать концепцию произведения и его свойства. Произведение — это результат умножения двух или более чисел.
Произведение может быть представлено в виде умножения: первый множитель умножается на второй множитель, и результатом будет произведение. Например, если у нас есть два числа — 4 и 3, и мы умножаем их, то получим произведение 12.
Произведение также можно представить с помощью повторяющегося сложения. Например, если у нас есть число 3 и мы умножаем его на 4, это означает, что мы должны прибавить 3 четыре раза: 3 + 3 + 3 + 3 = 12. Таким образом, 12 является произведением чисел 3 и 4.
Умножение имеет несколько свойств, которые помогают в решении задач. Например, свойство коммутативности гласит, что порядок множителей не влияет на результат умножения. То есть умножение числа 3 на 4 даст такой же результат, как и умножение числа 4 на 3.
Второй класс — это первый шаг в изучении произведения. Ученики будут узнавать больше о произведении и его свойствах по мере продвижения в математическом образовании.
Что такое произведение в математике 2 класс

Во втором классе ученики изучают произведение чисел от 1 до 10. Например, если мы умножим число 3 на число 4, то получим произведение 12. Это означает, что при сложении числа 3 четыре раза, мы получим результат 12.
Произведение можно записать с помощью умножения: 3 * 4 = 12. Здесь число 3 называется множителем, а число 4 – вторым множителем. Результат умножения называется произведением.
В математике произведение также имеет свойства. Например, свойство коммутативности гласит, что порядок множителей не влияет на результат умножения. То есть, 3 * 4 будет равно 4 * 3.
Второклассники изучают произведение чисел на уроках математики и решают примеры, чтобы закрепить свои знания. Например, они могут решить задачу: «Сколько будет 2 * 5?». Ответом будет произведение 10.
Изучение произведения во втором классе является важной основой для дальнейших математических навыков. Это поможет ученикам лучше понять понятие умножения и развить навыки работы с числами.
Определение произведения

Произведение двух чисел можно представить как сумму одного из чисел, взятого несколько раз. Например, произведение чисел 2 и 3 равно сумме двух чисел 2 + 2 + 2 = 6.
Произведение может быть использовано для нахождения площади прямоугольника или квадрата. Например, если длина прямоугольника равна 4, а ширина равна 3, то произведение этих двух чисел (4 × 3) даст площадь прямоугольника, равную 12.
Как считать произведение

Например, если мы хотим посчитать произведение чисел 5 и 3, мы умножаем эти числа:
5×3=15
Таким образом, произведение чисел 5 и 3 равно 15.
Можно также считать произведение большего количества чисел. Для этого нужно умножить все эти числа друг на друга. Например, если мы хотим посчитать произведение чисел 2, 3 и 4, мы выполняем следующие умножения:
2×3×4=24
Таким образом, произведение чисел 2, 3 и 4 равно 24.
Теперь вы знаете, как считать произведение чисел. Удачных вычислений!
Примеры вычисления произведения
-
- Пример 1: Вычислим произведение чисел 3 и 4.
Чтобы найти произведение 3 и 4, нужно умножить эти числа:
3 * 4 = 12
Ответ: произведение чисел 3 и 4 равно 12.
-
- Пример 2: Вычислим произведение чисел 5 и 2.
По аналогии с предыдущим примером, умножим числа 5 и 2:
5 * 2 = 10
Ответ: произведение чисел 5 и 2 равно 10.
-
- Пример 3: Вычислим произведение чисел 0 и 7.
Если одно из чисел равно нулю, то произведение всегда будет равно нулю:
0 * 7 = 0
Ответ: произведение чисел 0 и 7 равно 0.
Таким образом, вычисление произведения — это умножение двух или более чисел, результатом которого является новое число.
Свойства произведения
У произведения есть несколько свойств:
Свойство 1: Коммутативность
Произведение чисел не зависит от порядка их умножения. Например, 2 * 3 = 3 * 2. Это свойство можно запомнить так: «Менять местами числа — можно».
Свойство 2: Ассоциативность
При умножении трех и более чисел, результат не зависит от того, какие числа сначала перемножать. Например, (2 * 3) * 4 = 2 * (3 * 4). Это свойство можно запомнить так: «Скобки менять можно».
Свойство 3: Нейтральный элемент
Умножение на 1 не меняет число. Например, 2 * 1 = 2. Это свойство можно запомнить так: «Умножение на 1 не изменяет».
Свойство 4: Распределительное свойство
Произведение двух чисел, умноженное на третье число, равно произведению каждого числа, умноженного на это третье число. Например, 2 * (3 + 4) = (2 * 3) + (2 * 4). Это свойство можно запомнить так: «Через скобки вместо плюса можно поставить знак умножения».
Эти свойства помогают упростить вычисления и использовать их в различных задачах и примерах.
Произведение числа на 0
Произведение числа на 0 равно 0. Это означает, что если у нас есть любое число, а мы умножаем его на 0, то результат всегда будет равен 0.
Например, если у нас есть число 5 и мы умножаем его на 0, получаем:
5 * 0 = 0
Также можно провести эксперимент, умножив другие числа на 0 и увидеть, что результат всегда будет 0. Например:
12 * 0 = 0
100 * 0 = 0
Понимание этого правила поможет нам в решении математических задач, а также в понимании основных операций и свойств чисел.
Видео по теме:
Вопрос-ответ:
Какое определение произведения в математике во 2 классе?
Произведение в математике 2 класса — это результат умножения двух или более чисел.
Какими способами можно найти произведение?
Произведение можно найти с помощью сложения одного числа несколько раз или с помощью таблицы умножения.
Какие особенности имеет произведение в математике 2 класса?
Произведение в математике 2 класса обладает такими особенностями: коммутативность (порядок сомножителей не важен), ассоциативность (порядок выполнения умножений не важен), нейтральный элемент (единица не меняет значение числа при умножении).
Какие примеры произведения можно привести для уточнения понятия?
Примеры произведения в математике 2 класса: 2 * 3 = 6, 4 * 5 = 20, 3 * 3 * 3 = 27.
Какими методами можно учить детей произведение в математике 2 класса?
Для обучения произведению в математике 2 класса можно использовать игровые методы, задачи на нахождение произведения, таблицу умножения, а также примеры из реальной жизни для иллюстрации практического применения произведения.
Что такое произведение в математике?
Произведение — это результат умножения двух или более чисел. В математике оно является одной из основных арифметических операций.
Как вычислить произведение?
Для вычисления произведения нужно умножить два или более числа. Для этого можно использовать умножение в столбик или использовать знак умножения (*).
Произведение числа на 1
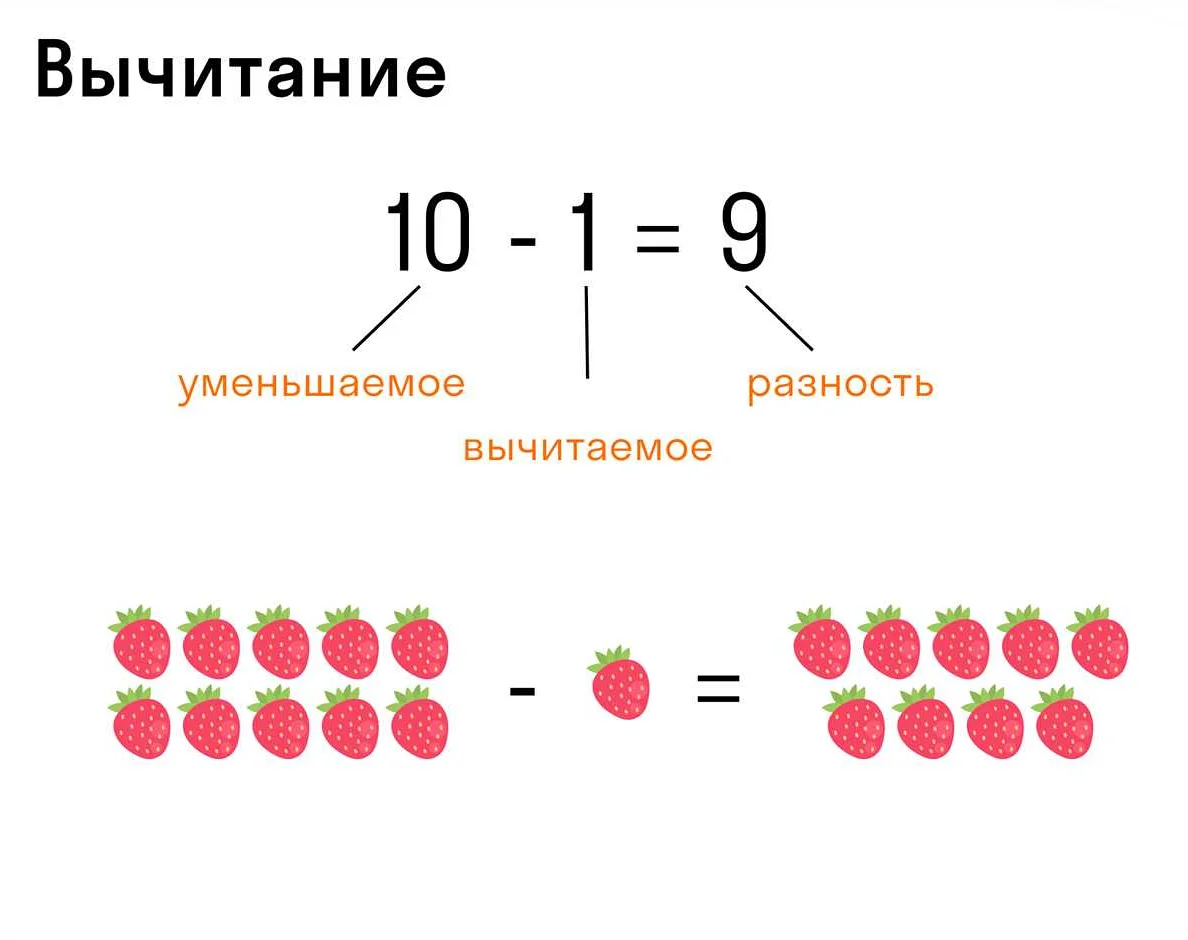
Произведение числа на 1 равно самому числу. Умножая любое число на 1, мы не изменяем его значение. Это свойство умножения на 1 называется свойством единицы.
Например, произведение числа 5 на 1 будет равно 5. Это можно записать как 5 * 1 = 5.
Также произведение числа 0 на 1 будет равно 0. Это можно записать как 0 * 1 = 0.
Понимание свойства единицы важно при решении задач и вычислениях, связанных с умножением.
Закрепление материала по произведению
Чтобы закрепить материал по произведению, давайте рассмотрим несколько примеров:
ПримерРешение
| 2 x 3 | 6 |
| 4 x 5 | 20 |
| 7 x 2 | 14 |
В каждом примере мы умножаем два числа и получаем произведение. Например, в первом примере 2 умножаем на 3 и получаем 6. Во втором примере 4 умножаем на 5 и получаем 20. А в третьем примере 7 умножаем на 2 и получаем 14.
Таким образом, произведение — это результат умножения двух чисел.




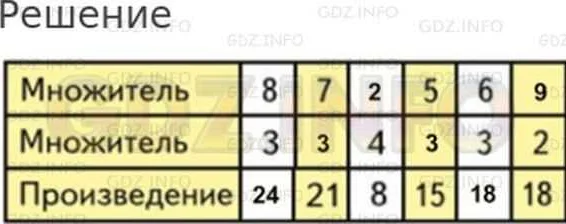
Произведение в математике для второго класса — это умножение чисел. Оно помогает нам узнать, сколько будет результат умножения двух чисел. Например, если у нас есть 2 корзины, и в каждой корзине 3 яблока, мы можем использовать произведение, чтобы узнать, сколько яблок у нас всего. Произведение 2 и 3 будет равно 6. То есть у нас будет 6 яблок. Помимо этого, произведение имеет свойства, например, коммутативное свойство, когда порядок чисел не важен. Например, если у нас есть 2 корзины с 3 яблоками и мы хотим узнать их суммарное количество, мы можем перемножить 3 на 2 и получить 6. Произведение — это важная математическая операция, которая помогает нам решать задачи и понимать мир вокруг нас.
Произведение в математике во втором классе — это одна из основных операций. Оно показывает, сколько будет результат, если одно и то же число прибавить несколько раз. Например, если у нас есть число 3 и мы его умножим на 4, то получим 12. Это значит, что мы прибавили число 3 четыре раза. Произведение можно обозначить знаком «×» или точкой, например: 3 × 4 = 12. Второклассники могут умножать числа до 10, используя таблицу умножения. Например, если нужно найти произведение 5 и 2, нужно посмотреть в таблицу умножения и найти пересечение строки 5 и столбца 2. В результате получим число 10. Таким образом, произведение позволяет нам быстро и точно узнать результат повторяющихся сложений и является важным навыком для дальнейшего изучения математики.
Очень понятная и доступная статья! Я с радостью прочитал и узнал новое о произведении в математике для второго класса. Теперь я понимаю, что произведение это результат умножения двух чисел. В статье очень хорошо объясняется, как умножать числа и как записывать произведение. Примеры с картинками помогли мне еще лучше понять материал. Теперь я смогу самостоятельно решать задачи на произведение. Большое спасибо автору за такую понятную статью!
Произведение — это одна из основных операций в математике. Во втором классе дети начинают изучать это понятие. Произведение обозначается знаком «×» или символом «*», и оно означает умножение двух чисел. Например, если у нас есть задача «4 × 3», то произведение этих чисел будет равно 12. Также важно помнить, что порядок умножения не влияет на результат. Например, «3 × 4» также будет равно 12. Произведение можно представить с помощью группировки объектов. Например, если у нас есть 3 коробки, в каждой из которых лежит по 4 яблока, то общее количество яблок будет равно произведению 3 и 4, то есть 12. Дети могут попробовать решить различные задачи с использованием произведения, например, посчитать количество яблок в нескольких корзинах или количество ног у нескольких животных. Понимание произведения поможет им лучше разобраться с умножением и решать более сложные задачи в будущем.