Что такое произвольное число в математике

Произвольное число в математике — это число, которое может быть выбрано из любого множества чисел без каких-либо ограничений. Оно может быть положительным или отрицательным, дробным или целым, вещественным или комплексным. Произвольное число играет важную роль в различных математических теориях и моделях, позволяя рассматривать диапазон возможных значений для различных переменных и функций.

Математика – это наука, изучающая структуру, свойства и отношения между числами, а также различные операции, которые можно производить с числами. В математике существуют различные типы чисел, и одним из них является произвольное число.

Произвольное число – это число, которое выбирается или определяется без каких-либо ограничений или специфических условий. Оно может принимать любое значение из определенного диапазона или быть выбрано среди всех возможных значений.

Произвольные числа широко используются в математике для решения задач и проведения исследований. Например, при решении уравнений или построении графиков функций часто приходится задавать произвольные значения переменных. При этом произвольное число может быть как целым, так и дробным, положительным или отрицательным.

Например, при решении уравнения 2x + 3 = 7, мы можем выбрать произвольное число для переменной x. Пусть x = 2. Подставляя это значение в уравнение, мы получим 2 * 2 + 3 = 7, что является верным утверждением. Однако, мы могли бы выбрать и другое произвольное число для x, например, x = 4. В этом случае, получаем 2 * 4 + 3 = 7, что также является верным утверждением. Таким образом, произвольные числа позволяют нам исследовать различные варианты решений и получать разнообразные результаты.

Определение произвольного числа

Произвольные числа часто используются для иллюстрации математических концепций или при проведении вычислений, где точное значение не имеет особого значения. Например, произвольное число может быть использовано в уравнении для представления неизвестного значения, которое нужно найти.

Примеры произвольных чисел:

• Произвольное целое число в диапазоне от 1 до 10.
• Произвольное вещественное число в интервале от -1 до 1.
• Произвольное число из множества {1, 2, 3, 4, 5}.

Важно отметить, что произвольные числа могут быть выбраны с помощью различных методов, таких как случайная генерация или задание пользователем. В математике и программировании использование произвольных чисел имеет широкий спектр применений.

Видео по теме:

Какое значение имеет произвольное число

Произвольное число в математике представляет собой число, выбранное без каких-либо ограничений или упорядочений. Оно может принимать любое значение из некоторого заданного множества чисел или быть выбрано случайным образом.

Значение произвольного числа может зависеть от контекста или задачи, в которой оно используется. В некоторых случаях произвольное число может быть заранее определено или задано в качестве параметра для дальнейших вычислений или анализа данных.

Примеры произвольных чисел могут включать выбор случайного числа от 1 до 10, выбор произвольной точки на координатной плоскости или выбор случайного элемента из некоторого множества. Все эти примеры демонстрируют, что произвольное число может принимать различные значения в зависимости от задачи или условий.

Примеры использования произвольных чисел

Произвольные числа широко применяются в математике и ее приложениях. Они играют важную роль в различных областях, включая алгебру, геометрию, теорию вероятностей и дискретную математику.

Например, в алгебре произвольные числа могут быть использованы для определения переменных в уравнениях и неравенствах. Мы можем рассмотреть уравнение вида x + 3 = 7, где x — произвольное число. Решая это уравнение, мы можем найти значение x как равное 4. Таким образом, произвольное число позволяет нам найти все возможные значения переменных, удовлетворяющих данному уравнению.

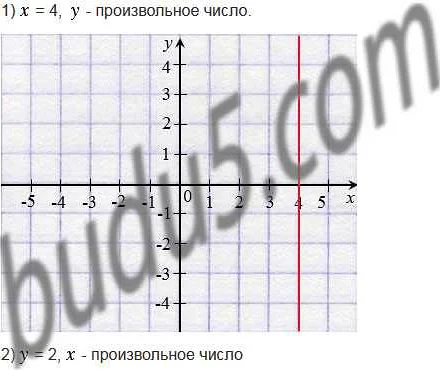
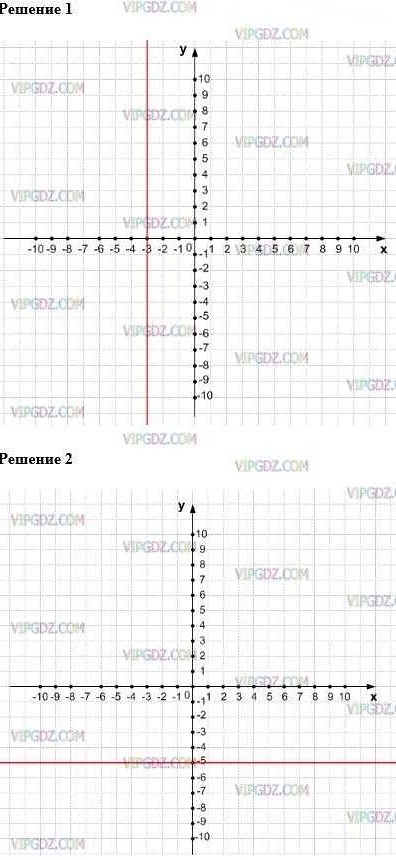
В геометрии произвольные числа могут быть использованы для задания координат точек на плоскости. Например, мы можем рассмотреть точку A с координатами (x, y), где x и y — произвольные числа. Таким образом, используя произвольные числа, мы можем определить широкий класс точек на плоскости.

В теории вероятностей произвольные числа могут быть использованы для моделирования случайных событий. Например, мы можем рассмотреть эксперимент, заключающийся в броске монеты. Пусть x — произвольное число, которое представляет результат броска монеты: 0 — орел, 1 — решка. Таким образом, используя произвольные числа, мы можем моделировать случайные события и исследовать их вероятности.

В дискретной математике произвольные числа могут быть использованы для создания комбинаторных моделей. Например, мы можем рассмотреть задачу о комбинации из n элементов, выбираемых по k элементов. Пусть x — произвольное число, которое представляет количество выбранных элементов. Таким образом, используя произвольные числа, мы можем исследовать различные комбинаторные модели и их свойства.

Таким образом, произвольные числа играют важную роль в математике и ее приложениях, позволяя нам моделировать различные ситуации, решать уравнения и изучать свойства различных математических объектов.

Вопрос-ответ:

Что такое произвольное число?

Произвольное число — это число, которое может принимать любое значение в определенном диапазоне или множестве. Оно не имеет ограничений и может быть любым числом в зависимости от контекста.

Как можно определить произвольное число?

Произвольное число можно определить, указав диапазон или множество, в котором оно может находиться. Например, если мы говорим о произвольном числе от 1 до 10, то оно может быть любым числом от 1 до 10, включительно.

Можете привести пример произвольного числа?

Конечно! Например, если мы говорим о произвольном числе от 1 до 100, то 42 может быть произвольным числом, так как оно находится в указанном диапазоне и может быть выбрано наугад.

В математике всегда используются произвольные числа?

Нет, не всегда. Использование произвольных чисел зависит от контекста и задачи. В некоторых случаях требуется использование конкретных чисел, а в других — произвольных чисел для получения общих решений или установления общих закономерностей.

Какие еще примеры произвольных чисел можно привести?

Еще один пример произвольного числа — это случайное число, которое выбирается наугад из определенного диапазона или множества. Например, если мы говорим о произвольном числе от 1 до 6, то любое число от 1 до 6 может быть выбрано случайным образом.

Что такое произвольное число в математике?

Произвольное число в математике — это число, которое выбирается без каких-либо ограничений или специальных условий. Оно может принимать любое значение из заданного множества чисел.

Какие примеры произвольных чисел можно привести?

Примеры произвольных чисел могут быть разнообразными. Например, если рассматривать множество всех натуральных чисел, то произвольным числом может быть любое число из этого множества, такое как 1, 10, 100 и т.д. Если рассматривать множество всех действительных чисел, то произвольным числом может быть любое число, например 3.14 или -2.5.

Значение произвольного числа в математических операциях

Произвольное число в математике представляет собой число, которое может быть любым из множества допустимых значений. Оно не имеет конкретного заданного значения, а может принимать любое значение в определенном диапазоне или множестве значений.

В математических операциях произвольное число может использоваться для демонстрации свойств и законов математики. Например, при сложении или вычитании произвольного числа с фиксированным числом, результат будет также произвольным числом.

При умножении произвольного числа на другое число, можно использовать произвольный множитель и получить произвольный результат. Также произвольное число может быть использовано для деления на другое число, что также даст произвольный результат.

Произвольное число может быть использовано в математических операциях для демонстрации свойств и законов математики, а также для решения задач и проблем, где требуется использовать случайные или неопределенные значения.

Произвольное число и его роль в статистике

Произвольное число в математике обычно определяется как число, которое выбирается без каких-либо ограничений или предписаний. В контексте статистики, произвольное число играет важную роль при проведении экспериментов и исследований.

В статистике, произвольное число может использоваться для выбора случайной выборки из генеральной совокупности. Например, чтобы провести опрос по мнению о политических предпочтениях, можно случайным образом выбрать несколько произвольных чисел, которые затем будут соответствовать определенным людям в генеральной совокупности.

Использование произвольных чисел в статистике помогает устранить возможные искажения и предвзятость, которые могут возникнуть при выборе выборки. Чтобы быть действительно представительным для генеральной совокупности, выборка должна быть случайной и не предсказуемой. Использование произвольных чисел помогает в достижении этой случайности и уменьшает вероятность систематической ошибки.

Кроме того, произвольные числа могут быть использованы для создания случайных переменных в статистических моделях. Например, при моделировании потока трафика на дороге, произвольные числа могут быть использованы для моделирования случайных событий, таких как появление автомобилей или изменение скорости движения.

Таким образом, произвольные числа играют важную роль в статистике, обеспечивая случайность и непредсказуемость в выборках и моделях. Их использование помогает достичь более точных и надежных результатов при проведении исследований и анализе данных.

Влияние произвольного числа на точность вычислений

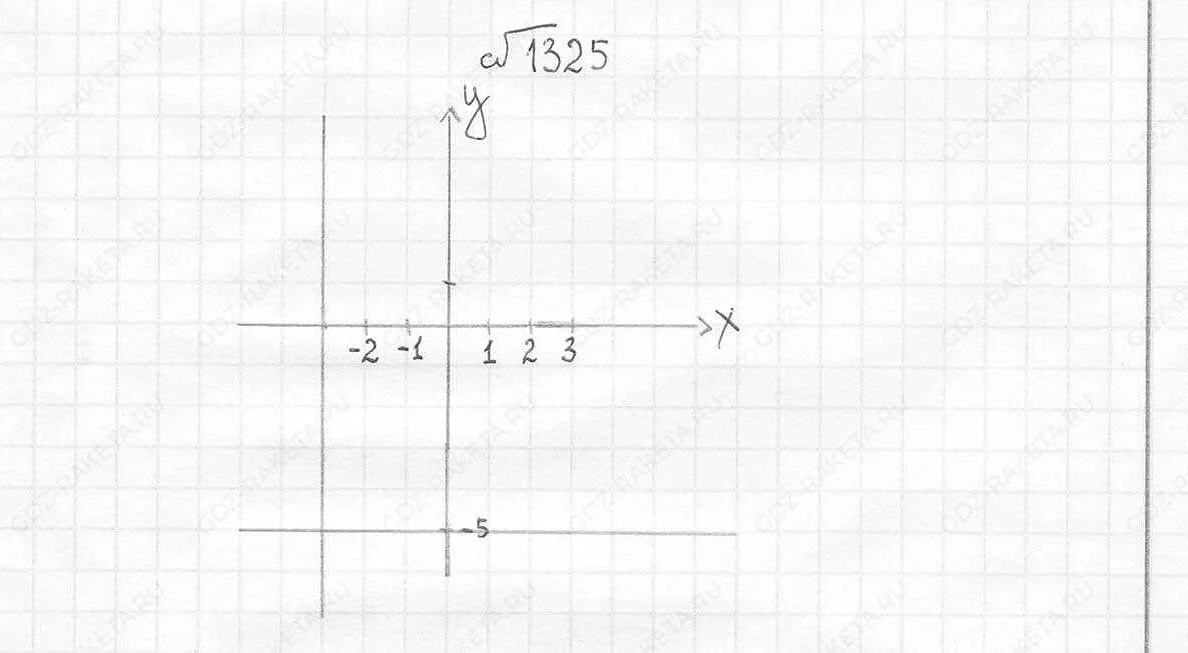
Произвольное число в математике представляет собой значение, которое может быть выбрано из некоторого диапазона или множества значений. Влияние произвольного числа на точность вычислений в математике может быть существенным.

При проведении вычислений в математике, особенно в численных методах, точность играет важную роль. Чем более точные значения используются в вычислениях, тем более точные будут результаты. Однако, если произвольное число, которое используется в вычислениях, не является достаточно точным, это может привести к неточным результатам.

Например, рассмотрим задачу вычисления площади круга. Формула для вычисления площади круга состоит из двух величин: радиуса круга и числа Пи. Если мы используем произвольное число для значения Пи, которое является приближением этой константы, то результат вычисления площади круга будет приближенным.

Точность вычислений может быть улучшена путем использования более точных значений произвольных чисел или увеличения количества разрядов при их представлении в вычислениях. Например, в вычислениях с плавающей точкой, использование чисел двойной точности может увеличить точность вычислений по сравнению с числами одинарной точности.

Влияние произвольного числа на точность вычислений зависит от конкретной задачи и используемого алгоритма. При выборе произвольного числа для вычислений следует учитывать требуемую точность и доступные ресурсы для ее достижения. Оптимальный выбор произвольного числа может быть основан на анализе конкретной задачи и опыте в области численных вычислений.

Приложения произвольных чисел в различных областях

Произвольные числа находят применение в различных областях науки и техники. Рассмотрим некоторые из них:

1. Криптография: Произвольные числа служат основой для создания криптографических ключей. Криптографический ключ представляет собой случайное число, которое используется для шифрования и дешифрования данных. Благодаря использованию произвольных чисел, криптографические ключи становятся непредсказуемыми и невоспроизводимыми, что обеспечивает высокую степень защиты информации.

2. Моделирование случайных процессов: В различных областях науки и техники необходимо моделировать случайные процессы, например, в физике, экономике, компьютерных симуляциях и т.д. Для этого используются произвольные числа, которые позволяют генерировать случайные последовательности чисел, приближающие статистические характеристики реальных случайных процессов.

3. Математические исследования: Произвольные числа играют важную роль в математике и ее различных областях. Например, в теории вероятностей и статистике произвольные числа используются для моделирования случайных событий и оценки вероятностей. В алгоритмах и компьютерных вычислениях произвольные числа используются для генерации псевдослучайных чисел, которые имеют свойства случайности, но при этом могут быть воспроизведены.

4. Информационная безопасность: Произвольные числа играют важную роль в обеспечении информационной безопасности. Они используются для создания случайных паролей и идентификаторов, генерации случайных чисел для шифрования данных и аутентификации пользователей. Благодаря использованию произвольных чисел, системы безопасности становятся непроницаемыми для взлома и подделки.

Таким образом, произвольные числа имеют широкий спектр применения в различных областях науки и техники, где требуется случайность, непредсказуемость и невоспроизводимость чисел.

Выводы и обзор использования произвольных чисел в математике

Произвольные числа представляют собой числа, которые могут принимать любое значение в заданном диапазоне или наборе значений. Они используются в математике для моделирования случайных событий, а также для решения задач, где точное значение недоступно или неизвестно.

Произвольные числа широко используются в статистике, вероятности, теории игр и других областях математики. Они позволяют моделировать различные случаи и предсказывать вероятности исходов в экспериментах.

Одним из примеров использования произвольных чисел является моделирование случайной выборки из заданного распределения. Например, при проведении опроса среди населения можно использовать произвольные числа для случайного отбора опрашиваемых.

Также произвольные числа могут использоваться для моделирования случайных величин, таких как время ожидания, расстояние, сумма денег и т. д. Это позволяет анализировать и предсказывать различные ситуации и варианты развития событий.

Произвольные числа также играют важную роль в компьютерных моделях и симуляциях. Они используются для генерации случайных чисел, что позволяет создавать разнообразные условия и варианты виртуального мира.

В заключение, использование произвольных чисел в математике является неотъемлемой частью моделирования случайных событий и предсказания вероятностей. Они помогают решать задачи, где точное значение недоступно или неизвестно, и позволяют анализировать и предсказывать различные ситуации и исходы экспериментов.