Что такое простые множители 6 класс математика

Простые множители в математике для 6 класса — это числа, которые делят данное число без остатка и сами не делятся на другие числа, кроме 1 и себя самого. Узнайте, как найти простые множители и использовать их в задачах и уравнениях.

Простые множители – это числа, которые делят данное число без остатка и сами делятся только на 1 и на себя. Простые множители играют важную роль в разложении чисел на множители и нахождении их наибольшего общего делителя.

Основное понятие, используемое при работе с простыми множителями, — это факторизация числа. Факторизация представляет число в виде произведения простых множителей. Например, число 24 можно разложить на простые множители как 2 * 2 * 2 * 3.

Простые множители помогают нам легко и быстро находить наибольший общий делитель двух чисел. Например, чтобы найти наибольший общий делитель чисел 36 и 48, мы разложим оба числа на простые множители: 36 = 2 * 2 * 3 * 3, а 48 = 2 * 2 * 2 * 2 * 3. Теперь мы можем сравнить простые множители и выбрать их наименьшую степень, получив наибольший общий делитель – 2 * 2 * 3 = 12.

Простые множители широко используются в различных областях математики, физики и информатики. Умение разложить число на простые множители позволяет решать множество задач и находить наибольший общий делитель, наименьшее общее кратное и другие важные параметры чисел.

О чем будет речь в статье

В данной статье мы рассмотрим понятие простых множителей в математике для учеников 6 класса. Мы изучим, что такое простые числа и как их находить. Также мы узнаем, что такое простые множители и как их использовать для разложения чисел на множители. Рассмотрим основные примеры разложения чисел на простые множители и научимся применять это знание на практике. По окончанию чтения статьи ученики смогут легко разложить число на простые множители и использовать это знание в решении задач по математике.

Для наглядности и удобства изучения материала в статье будут представлены таблицы с примерами разложения чисел на простые множители.

ЧислоПростые множители

12	2, 2, 3
20	2, 2, 5
36	2, 2, 3, 3

Также мы рассмотрим несколько задач, в которых потребуется использовать знания о простых множителях для решения. Это поможет ученикам применить полученные знания на практике и закрепить материал.

Все материалы в статье будут представлены доступным и понятным языком, что позволит ученикам легко усвоить информацию и применить ее в учебе.

Определение простых множителей

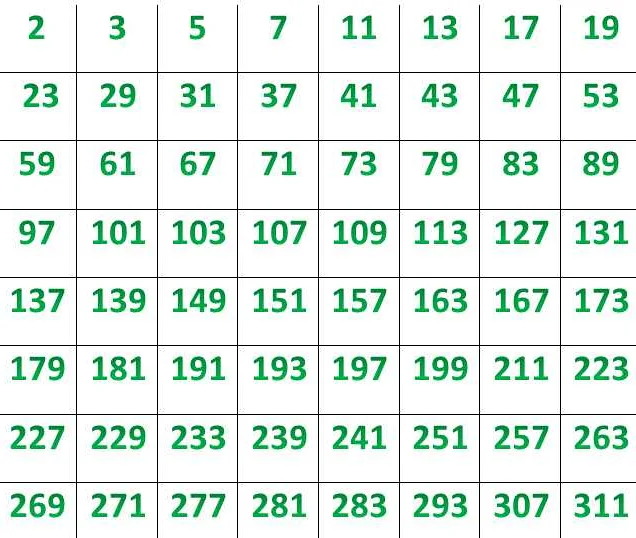
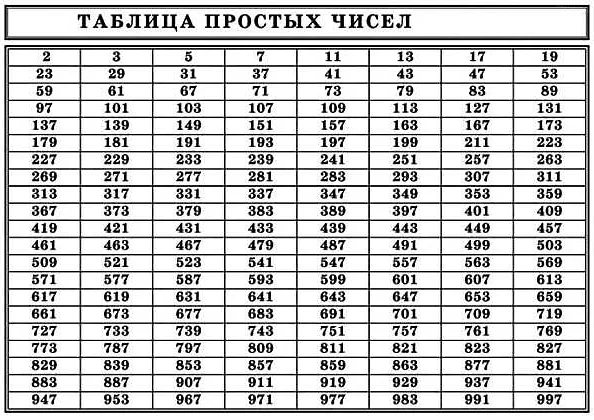
Простое число — это число, которое делится без остатка только на себя и на 1. Примеры простых чисел: 2, 3, 5, 7, 11 и т.д.

Чтобы найти простые множители данного числа, его необходимо последовательно делить на простые числа, начиная с 2. Если число делится без остатка, то это число является простым множителем. Затем полученный результат снова делим на простые числа и так далее, пока результат деления не станет равным 1.

Например, чтобы найти простые множители числа 24, мы начинаем делить его на 2:

24 ÷ 2 = 12

Затем делим полученное число на 2:

12 ÷ 2 = 6

Последний шаг:

6 ÷ 2 = 3

Результат равен 3, что является простым числом. Таким образом, простые множители числа 24 это 2, 2 и 3.

Основные понятия

Простое число — это число, которое делится только на 1 и на само себя.

Разложение числа на простые множители — это представление данного числа в виде произведения простых чисел.

Нахождение простых множителей числа — это процесс разложения данного числа на простые множители.

НОД (наибольший общий делитель) — это наибольшее число, на которое одновременно делится данный набор чисел.

НОК (наименьшее общее кратное) — это наименьшее число, которое одновременно делится на данный набор чисел.

Примеры простых множителей

Простыми множителями числа называются числа, на которые это число делится без остатка. Рассмотрим некоторые примеры простых множителей:

Пример 1:

Число 12 имеет простые множители 2 и 3, так как 12 делится на 2 и 3 без остатка:

12 = 2 * 2 * 3

Пример 2:

Число 15 имеет простые множители 3 и 5, так как 15 делится на 3 и 5 без остатка:

15 = 3 * 5

Пример 3:

Число 24 имеет простые множители 2 и 3, так как 24 делится на 2 и 3 без остатка:

24 = 2 * 2 * 2 * 3

Пример 4:

Число 35 имеет простые множители 5 и 7, так как 35 делится на 5 и 7 без остатка:

35 = 5 * 7

Это лишь некоторые примеры простых множителей. Каждое число имеет свои уникальные простые множители, которые можно найти путем деления числа на все возможные числа до его половины и проверки на делимость без остатка.

Пример 1

Разложим число 48 на простые множители.

Сначала найдем наименьший простой делитель числа 48. Он равен 2, так как число 48 делится на 2 без остатка.

Поделим число 48 на 2. Получим 48 ÷ 2 = 24.

Теперь найдем наименьший простой делитель числа 24. Он также равен 2.

Поделим число 24 на 2. Получим 24 ÷ 2 = 12.

Продолжим делить число 12 на наименьший простой делитель, который равен 2.

Получим 12 ÷ 2 = 6.

Теперь число 6 уже не делится на 2 без остатка, поэтому найдем следующий наименьший простой делитель, который равен 3.

Поделим число 6 на 3. Получим 6 ÷ 3 = 2.

Делить число 2 на простой делитель уже не имеет смысла, так как это сам простой делитель.

Итак, разложение числа 48 на простые множители: 48 = 2 × 2 × 2 × 2 × 3 = 2^4 × 3.

Пример 2

Разложим число 36 на простые множители:

1. Находим первый простой делитель числа 36. Перебираем простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 и т.д. Первое простое число, на которое делится 36 без остатка, — это 2.
2. Делим число 36 на 2 и получаем 18.
3. Затем находим следующий простой делитель числа 18. Перебираем простые числа, начиная с 2, и находим, что 18 делится без остатка на 2.
4. Делим число 18 на 2 и получаем 9. В данном случае 9 — простое число.
5. Таким образом, разложение числа 36 на простые множители выглядит следующим образом: 36 = 2 * 2 * 3 * 3.

Простые множители числа 36: 2 и 3.

Пример 3

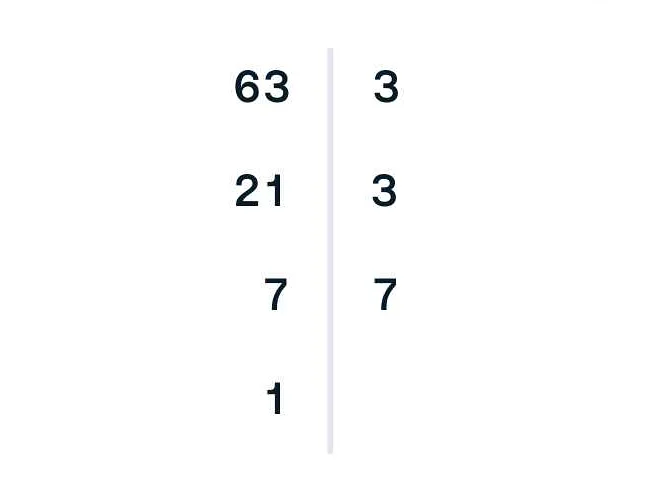
Разложим число 36 на простые множители.

Для начала проверяем, делится ли число на 2. Да, 36 делится на 2 без остатка.

36 ÷ 2 = 18

Получили число 18. Теперь проверяем, делится ли оно на 2. Да, 18 делится на 2 без остатка.

18 ÷ 2 = 9

Получили число 9. Теперь проверяем, делится ли оно на 2. Нет, 9 не делится на 2 без остатка.

Проверяем, делится ли 9 на 3. Да, 9 делится на 3 без остатка.

9 ÷ 3 = 3

Получили число 3. Дальше проверяем, делится ли оно на 2. Нет, 3 не делится на 2 без остатка.

Проверяем, делится ли 3 на 3. Да, 3 делится на 3 без остатка.

3 ÷ 3 = 1

Получили число 1. Дальше проверять уже не нужно. Мы разложили число 36 на простые множители:

Простые множителиСтепени

2	2
3	2

Свойства простых множителей

Свойства простых множителей:

1. Каждое число можно представить в виде произведения простых множителей. Например, число 12 можно представить как 2 * 2 * 3.
2. Простые множители числа могут повторяться. Например, число 36 можно представить как 2 * 2 * 3 * 3.
3. Простые множители числа не зависят от порядка умножения. Например, число 20 можно представить как 2 * 2 * 5 или 2 * 5 * 2.
4. Если число является простым, то у него только один простой множитель – оно само. Например, число 17 имеет только один простой множитель – число 17.
5. Если число делится на простое число без остатка, то это число является одним из простых множителей данного числа. Например, число 24 делится на 2 без остатка, поэтому 2 является одним из простых множителей числа 24.

Знание свойств простых множителей поможет в решении задач по факторизации чисел и нахождению их наименьшего общего кратного и наибольшего общего делителя.

Свойство 1

Например, число 12 можно разложить на простые множители 2 и 3, так как 2 * 2 * 3 = 12. При этом, ни 2, ни 3 нельзя разложить на множители более маленькие, чем они сами.

Используя простые множители, мы можем записать число в виде произведения простых множителей. Например, число 24 можно записать как 2 * 2 * 2 * 3.

Разложение числа на простые множители позволяет упростить вычисления и проводить операции с числами более эффективно.

Свойство 2

Это свойство простых множителей позволяет упростить деление чисел с помощью их разложения на простые множители. Если числа имеют общие простые множители, то их можно сократить и упростить выражение.

Например, чтобы упростить выражение 12/18, можно разложить числа на простые множители: 12 = 2 * 2 * 3, 18 = 2 * 3 * 3. После сокращения общих простых множителей получим: 12/18 = (2 * 2 * 3)/(2 * 3 * 3) = 1/3.

Таким образом, знание свойства простых множителей позволяет упростить арифметические операции и решать задачи на деление и умножение чисел.

Видео по теме:

Какое значение имеет понятие «простые множители» в математике?

Простые множители — это числа, на которые можно разложить данное число без остатка. Они являются основными строительными блоками для составления чисел и имеют особое значение в теории чисел.

Как найти простые множители числа?

Для нахождения простых множителей числа нужно начать с наименьшего простого числа (обычно это число 2) и проверять, делится ли число на это число без остатка. Если делится, то это является простым множителем. Затем число нужно поделить на найденный простой множитель и продолжить процесс для полученного частного.

Зачем нужно разложение числа на простые множители?

Разложение числа на простые множители позволяет нам лучше понять его структуру и свойства. Это основа для решения многих задач в математике, таких как нахождение наибольшего общего делителя, наименьшего общего кратного, нахождение простых чисел, проверка чисел на простоту и т.д.

Можно ли разложить число на простые множители, если оно само является простым?

Если число само является простым, то его разложение на простые множители будет состоять только из этого числа. Например, число 7 является простым и его разложение на простые множители будет выглядеть так: 7 = 7.