Что такое простой делитель в математике
Содержимое
- 1 Что такое простой делитель в математике
- 1.1 Определение простого делителя
- 1.2 Свойства простого делителя
- 1.3 Примеры простого делителя
- 1.4 Как найти простой делитель
- 1.5 Простые делители в разложении числа
- 1.6 Простой делитель и множественность
- 1.7 Простой делитель и делимость
- 1.8 Вопрос-ответ:
- 1.8.0.1 Что такое простой делитель в математике?
- 1.8.0.2 Какие свойства имеют простые делители?
- 1.8.0.3 Как найти простые делители числа?
- 1.8.0.4 Какие примеры простых делителей можно привести?
- 1.8.0.5 Может ли число иметь только один простой делитель?
- 1.8.0.6 Что такое простой делитель?
- 1.8.0.7 Какие свойства имеют простые делители?
- 1.9 Простой делитель и наименьшее общее кратное
- 1.10 Видео по теме:
Простой делитель — это число, которое делит данное число нацело и не имеет других делителей, кроме единицы и самого себя. Узнайте, как находить простые делители и на что они могут повлиять в математике.
Простой делитель — одно из основных понятий в теории чисел. Это натуральное число, которое делит данное число нацело и не имеет делителей, кроме 1 и самого себя. Простые делители играют важную роль в различных математических исследованиях и прикладных задачах.
Свойства простых делителей являются основными в теории чисел. Одно из основных свойств простых делителей заключается в том, что любое натуральное число может быть представлено в виде произведения простых чисел. Это так называемая факторизация числа.
Например, число 12 может быть разложено на простые множители: 12 = 2 * 2 * 3.
Простые делители также позволяют определить наибольший общий делитель двух чисел и наименьшее общее кратное. Наибольший общий делитель — это наибольшее число, которое делит оба числа нацело, а наименьшее общее кратное — это наименьшее число, которое делится на оба числа нацело.
Определение простого делителя
Например, число 7 является простым делителем числа 21, так как 7 делит 21 без остатка и имеет только два делителя: 1 и 7.
Простые делители играют важную роль в различных областях математики, таких как факторизация чисел и построение простых чисел.
Свойства простого делителя
Вот некоторые свойства простого делителя:
- Простой делитель всегда является делителем самого числа. Например, число 7 является простым делителем числа 42, так как 42 делится на 7 без остатка.
- Простой делитель всегда меньше или равен самому числу. Например, простые делители числа 15 — это 3 и 5, которые оба меньше самого числа 15.
- Простой делитель не может быть представлен в виде произведения двух или более простых чисел. Например, число 10 имеет простые делители 2 и 5, которые нельзя представить в виде произведения других простых чисел.
- Простой делитель не может быть делителем другого простого делителя. Например, числа 2 и 3 являются простыми делителями числа 12, но 2 не является делителем 3 и наоборот.
- Простой делитель всегда имеет только два делителя — 1 и самого себя. Например, простой делитель числа 11 имеет только два делителя — 1 и 11.
Знание свойств простых делителей позволяет более эффективно решать задачи, связанные с дроблениями чисел на простые множители и нахождением их наименьшего общего кратного и наибольшего общего делителя.
Примеры простого делителя
Пример 1: Число 7. Единственные делители этого числа — 1 и 7, поэтому 7 является простым делителем.
Пример 2: Число 13. У него также только два делителя — 1 и 13, следовательно, 13 является простым делителем.
Пример 3: Число 19. Простые делители этого числа — 1 и 19, поэтому 19 является простым делителем.
Пример 4: Число 23. Единственные делители этого числа — 1 и 23, поэтому 23 также является простым делителем.
Простые делители играют важную роль в различных областях математики, таких как теория чисел и криптография. Они помогают в решении различных задач и имеют множество интересных свойств, которые изучают математики.
Как найти простой делитель
Один из самых простых способов найти простой делитель — это последовательно делить число на все числа от 2 до его квадратного корня. Если деление происходит без остатка, то число является простым делителем. Если найден простой делитель, то можно остановить дальнейший поиск.
Например, для числа 28 можно последовательно делить его на числа от 2 до 5 (квадратный корень из 28). Первое деление без остатка произойдет при делении на 2, значит 2 — простой делитель числа 28.
Еще один метод поиска простого делителя — это применение алгоритма решета Эратосфена. Данный алгоритм позволяет найти все простые числа до заданного числа. Зная простые числа до заданного числа, можно проверить, является ли это число простым делителем.
Например, для числа 28 можно использовать решето Эратосфена для поиска всех простых чисел до 28. Из полученного списка простых чисел можно выбрать только те числа, которые являются делителями числа 28. В данном случае получим простые делители 2 и 7.
Таким образом, существует несколько методов и алгоритмов, с помощью которых можно найти простой делитель числа. Выбор метода зависит от конкретной задачи и доступных ресурсов для решения.
Простые делители в разложении числа
Для разложения составных чисел на простые делители используется процесс факторизации. Факторизация позволяет представить число в виде произведения простых множителей.
Например, число 20 можно разложить на простые делители следующим образом: 20 = 2 * 2 * 5. Здесь число 2 и 5 являются простыми делителями числа 20.
Таким образом, любое число можно представить в виде произведения простых чисел, называемых простыми делителями. Это позволяет упростить вычисления и изучение свойств чисел.
Простой делитель и множественность

Множественность простого делителя — это степень, в которой простое число входит в разложение данного числа на простые множители.
Например, для числа 12 его разложение на простые множители будет выглядеть следующим образом: 22 * 3. Здесь простое число 2 входит в разложение числа 12 с множественностью 2, так как оно присутствует в разложении два раза.
Множественность простого делителя позволяет определить, сколько раз данный простой делитель входит в разложение числа на простые множители.
Знание множественности простого делителя может быть полезно, например, при упрощении дробей, факторизации чисел или решении уравнений.
Простой делитель и делимость

Делимость – это свойство, которое означает, что одно число делится на другое без остатка. Если число а делится на число b без остатка, то число b является делителем числа а.
Простые делители являются основными строительными блоками в разложении чисел на множители. Каждое натуральное число может быть разложено на простые множители. Например, число 12 может быть разложено на простые множители 2, 2 и 3.
Простые делители обладают несколькими интересными свойствами:
- Простые числа не могут быть выражены в виде произведения двух или более натуральных чисел, кроме как в виде произведения на 1.
- Каждое натуральное число имеет единственное разложение на простые множители. Это означает, что простые делители числа уникальны.
- Если число делится на простое число без остатка, то это число либо само является простым делителем, либо может быть разложено на простые делители.
Простые делители играют важную роль в различных областях математики, таких как теория чисел, криптография и алгоритмы.
Вопрос-ответ:
Что такое простой делитель в математике?
Простой делитель — это натуральное число, которое делит данное число без остатка и само имеет только два делителя: 1 и само себя.
Какие свойства имеют простые делители?
Простые делители обладают следующими свойствами: они всегда натуральные числа, они делят число без остатка, и они сами имеют только два делителя.
Как найти простые делители числа?
Для поиска простых делителей числа можно использовать метод факторизации или деление числа на все числа от 2 до квадратного корня из числа.
Какие примеры простых делителей можно привести?
Примеры простых делителей: для числа 10 — это 2 и 5; для числа 15 — это 3 и 5; для числа 23 — это только число 23, так как оно само является простым.
Может ли число иметь только один простой делитель?
Нет, число не может иметь только один простой делитель. Простой делитель всегда имеет только два делителя: 1 и само себя.
Что такое простой делитель?
Простой делитель — это натуральное число, которое делит данный натуральный число без остатка и является простым числом.
Какие свойства имеют простые делители?
Простые делители имеют несколько свойств. Во-первых, каждое натуральное число, большее единицы, имеет как минимум один простой делитель. Во-вторых, если простое число p делит произведение двух чисел a и b, то оно делит хотя бы один из них. В-третьих, если простое число p делит произведение a и b, то оно делит a или b (или оба). В-четвертых, если простое число p делит квадрат натурального числа, то оно делит само это число.
Простой делитель и наименьшее общее кратное
Наименьшее общее кратное (НОК) двух или более чисел это наименьшее число, которое делится на все эти числа без остатка. Например, НОК чисел 4 и 6 равно 12.
Простые делители и НОК тесно связаны. Если у нас есть два числа, то их НОК можно найти, используя простые делители и степени этих делителей.
Для нахождения НОК нужно взять все простые делители каждого числа и учесть максимальные степени этих делителей. Например, для чисел 8 и 12:
8 = 2^3
12 = 2^2 * 3
Максимальные степени простого делителя 2 равны 3 и 2, а простого делителя 3 равны 0 и 1. Поэтому НОК равно 2^3 * 3 = 24.
Таким образом, простые делители помогают нам находить наименьшее общее кратное двух или более чисел.

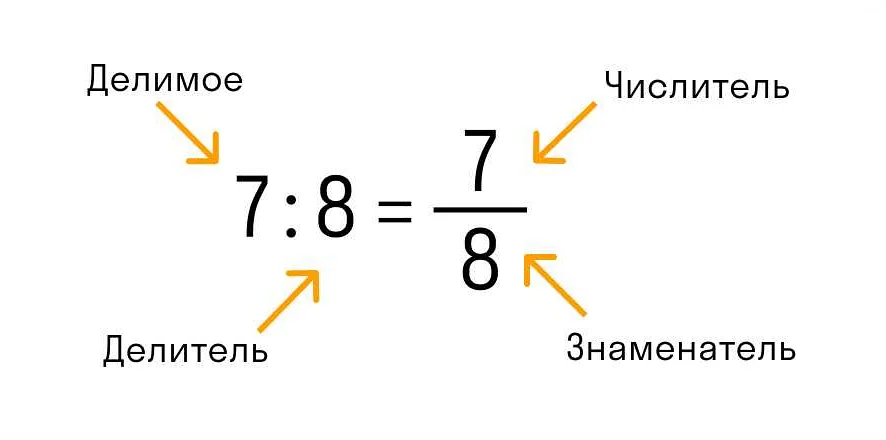

Очень интересная и познавательная статья! Я всегда задавался вопросом, что такое простой делитель и как его определить. Спасибо автору за четкое объяснение! Теперь я понимаю, что простой делитель — это натуральное число, которое не имеет делителей, кроме себя и единицы. Важно отметить, что простые делители несут важную информацию о свойствах чисел, их роли можно сравнить с «кирпичиками», из которых составляются все остальные числа. Зная простые делители, мы можем разложить любое число на простые множители, что упрощает работу с числами и решение различных задач. Например, факторизация чисел помогает нам находить НОД и НОК, а также решать уравнения и системы уравнений. Ясные и понятные примеры в статье помогли мне лучше усвоить материал. В целом, статья очень полезна и рекомендую ее всем, кто интересуется математикой!
Ваша статья очень понятно объясняет, что такое простой делитель в математике. Я всегда думала, что делителей у чисел много, но благодаря вашему объяснению я поняла, что простые делители — это особые числа, которые делят число без остатка и сами являются простыми числами. Мне очень понравилось, что вы привели примеры, чтобы наглядно показать, как найти простые делители. Теперь я легко понимаю, что такое простые числа и как их использовать при разложении числа на простые множители. Спасибо за четкое объяснение и полезные примеры! Я буду рада прочитать еще статьи на вашем сайте.
Простой делитель в математике — это такой делитель натурального числа, который не имеет других делителей, кроме единицы и самого себя. Это понятие очень важно для многих областей математики, включая алгебру и теорию чисел. Простые делители помогают нам разложить сложные числа на их простые множители и понять их структуру. Кроме того, они играют важную роль в решении задач, связанных с делимостью. Например, возьмем число 24. Его простыми делителями являются числа 2, 3 и 6. Это значит, что 24 можно разложить на произведение простых чисел: 2 * 2 * 2 * 3. Такое разложение называется каноническим разложением числа. Простые делители имеют несколько важных свойств. Во-первых, каждое натуральное число можно разложить на простые множители единственным образом. Во-вторых, простые числа являются основными строительными блоками для всех остальных чисел. Например, любое число можно представить в виде произведения простых чисел, возведенных в некоторые степени. Понимание простых делителей помогает нам решать различные математические задачи. Они используются, например, для нахождения наибольшего общего делителя, проверки чисел на простоту и многих других задач. Изучение простых делителей позволяет нам получить глубокий аналитический взгляд на мир чисел и открыть новые закономерности и связи.
Прекрасная статья! Очень интересно узнать о простых делителях в математике. Я всегда думала, что делители это просто числа, на которые можно разделить другое число без остатка. Но теперь я понимаю, что простые делители имеют особое значение. Они являются числами, которые делят наше число только на себя и на единицу. Это такая интересная концепция! Я поняла, что простые делители играют важную роль в факторизации чисел и нахождении наименьшего общего делителя. И узнать, что простые числа бесконечны, просто поразительно! Теперь я с нетерпением буду искать простые делители в числах, чтобы лучше понять их структуру. Спасибо за такую понятную и информативную статью!
Отличная статья! Я всегда была сильно заинтересована в математике, и простые делители — одно из самых увлекательных понятий для меня. Теперь я понимаю, что простые делители — это числа, которые делятся без остатка только на себя и на единицу. Их свойства также очень интересны: они всегда являются простыми числами, и их количество в числе может быть как конечным, так и бесконечным. Мне понравилось, как автор привел примеры, чтобы проиллюстрировать понятие простых делителей. Теперь я понимаю, что они встречаются везде в нашей повседневной жизни, от разложения чисел на простые множители до защиты информации в криптографии. Эта статья увлекательна и понятна даже для людей, не имеющих специального образования в математике. Спасибо за такое интересное чтение!