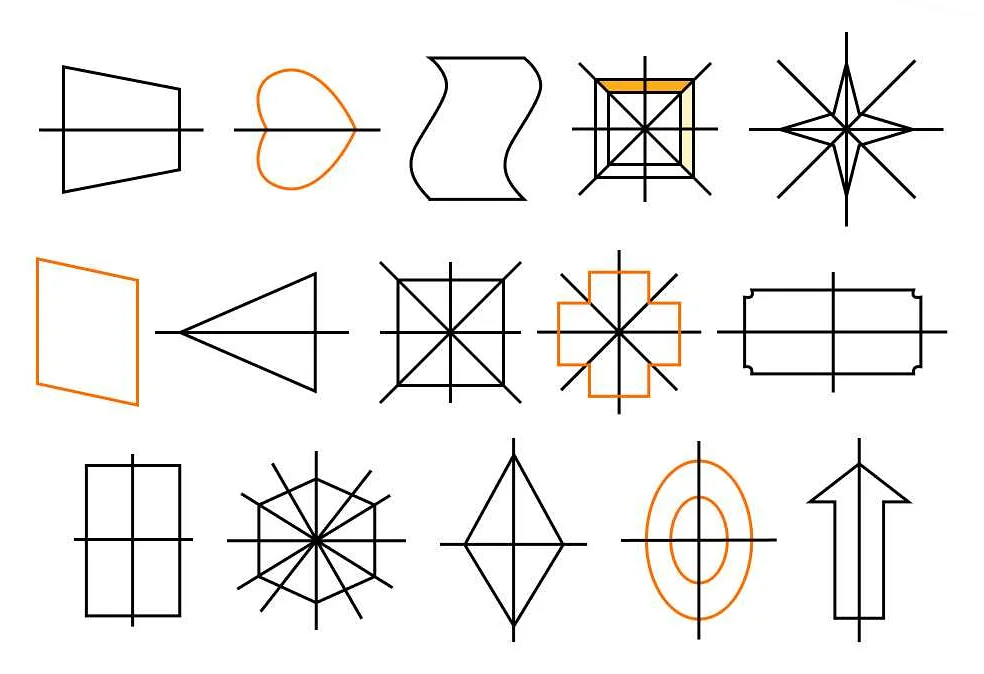Что означает симметрично в математике

Симметрия в математике означает, что объект или график может быть разделен на две одинаковые части относительно определенной прямой, плоскости или точки. Эта статья объясняет понятие симметрии и приводит примеры его применения в математических задачах и графиках.

Симметрия — одно из основных понятий в математике. Она является ключевым элементом для понимания многих математических концепций и теорий. Симметричные объекты имеют особые характеристики, которые позволяют нам легко анализировать их свойства и отношения.

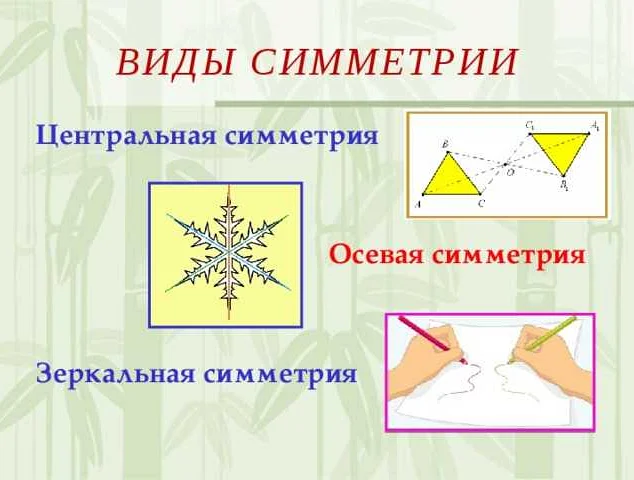
В математике симметрия может быть определена как отношение между объектами, которое означает, что один объект может быть преобразован в другой с помощью определенного преобразования. Это может быть отражение, поворот или сдвиг. Преобразование, сохраняющее симметрию, называется симметрией объекта.

Симметрия имеет широкое применение в различных областях математики, физики и искусства. Например, в геометрии симметрия используется для изучения фигур и форм, а в алгебре — для анализа уравнений и функций. В физике симметрия объясняет законы сохранения и принципы преобразования. В искусстве симметрия создает гармоничные и привлекательные композиции.

Примером симметрии может служить отражение фигуры относительно оси. Если каждая точка фигуры, отображаемая на оси, имеет симметричную точку относительно нее, то фигура считается симметричной относительно этой оси. Примерами таких симметричных фигур могут служить квадрат, прямоугольник, равносторонний треугольник и многие другие.

Симметрично в математике: определение и примеры

В математике понятие симметричности широко используется для описания отношений и структур объектов. Симметричность обычно означает, что некоторый объект или отношение сохраняется при некоторых преобразованиях.

Один из наиболее распространенных видов симметрии в математике — это симметрия относительно оси. Например, если взять двумерную фигуру, такую как круг, и нарисовать ось, проходящую через его центр, то фигура будет симметрична относительно этой оси. Это означает, что если отразить фигуру вдоль оси, то она не изменится.

Кроме того, симметрия может быть определена в отношении других преобразований, таких как повороты и смещения. Например, если взять треугольник и повернуть его на 120 градусов вокруг его центра, то он будет симметричен. Это означает, что после поворота треугольник будет выглядеть точно так же, как и до поворота.

Симметричность также может быть определена в отношении алгебраических операций. Например, если взять два числа и сложить их, то результат будет симметричен относительно этих чисел. Это означает, что порядок слагаемых не имеет значения, и сумма будет одинаковой вне зависимости от порядка сложения.

Таким образом, симметрия в математике является важным понятием, которое помогает описать и анализировать различные структуры и отношения между объектами.

Видео по теме:

Понятие симметричности в математике

Одним из простых примеров симметричности является отношение равенства для чисел. Например, число 4 симметрично самому себе, так как после отражения оно остается неизменным. Также, если два числа равны друг другу, то они также симметричны относительно друг друга.

Симметричность также может быть применена к геометрическим фигурам. Например, квадрат является симметричной фигурой, так как его можно отразить относительно любой из своих диагоналей и он останется идентичным. Также, если две фигуры идентичны, то они симметричны относительно друг друга.

Понятие симметричности также широко используется в алгебре, где симметричность может быть определена в терминах отношений и операций. Например, если для двух элементов выполняется операция сложения и результат равен нулю, то эти элементы симметричны относительно операции сложения.

Симметричные фигуры и объекты

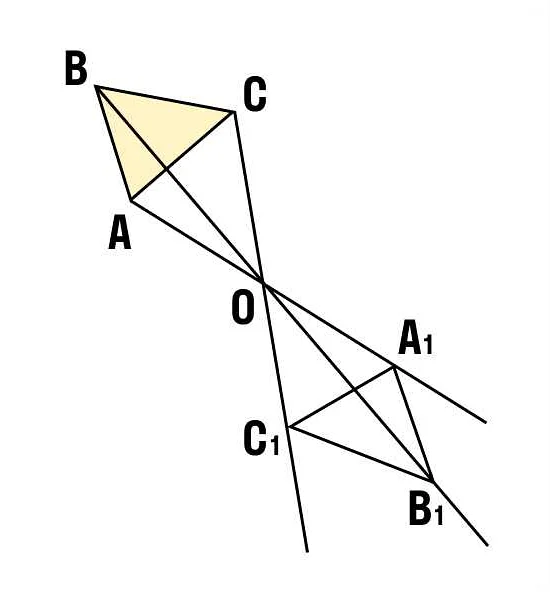
Симметричные фигуры могут быть как плоскими, так и пространственными. Некоторые примеры симметричных фигур включают прямоугольник, квадрат, круг, равносторонний треугольник и многоугольник. Все эти фигуры имеют ось симметрии, которая является прямой или плоскостью, вокруг которой фигура симметрична.

Кроме того, симметрия может применяться не только к геометрическим фигурам, но и к другим объектам. Например, симметричные молекулы в химии имеют оси симметрии, вокруг которых можно поворачивать молекулу так, чтобы она выглядела одинаково.

Симметрия является важным концептом в математике, так как она позволяет нам анализировать и классифицировать фигуры и объекты. Понимание симметрии помогает нам увидеть закономерности и свойства, которые могут быть полезными при решении различных задач и проблем.

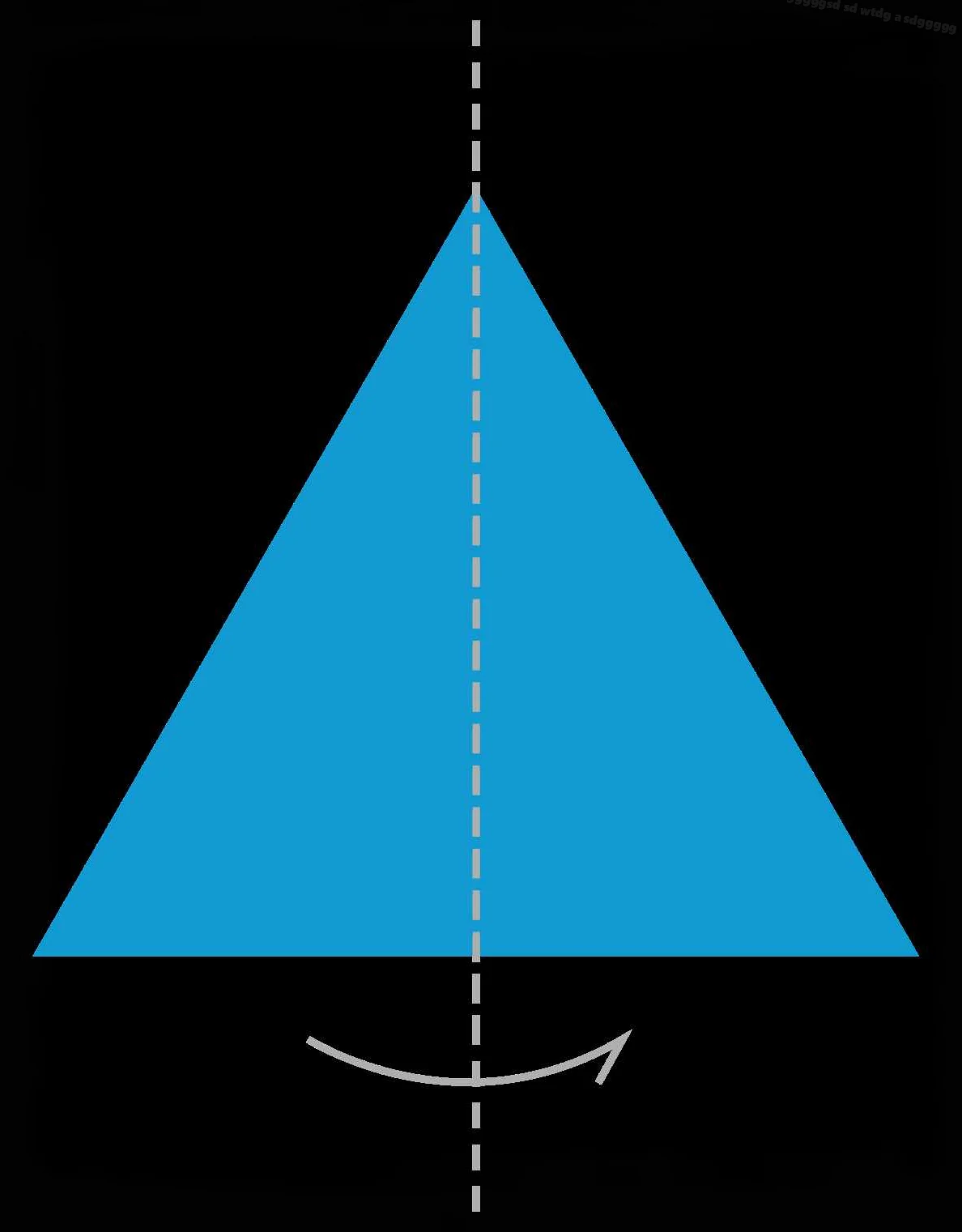
Оси симметрии

Горизонтальная ось симметрии проходит через центр фигуры и делит ее на две симметричные половины, которые совпадают при отражении относительно этой оси.

Вертикальная ось симметрии также проходит через центр фигуры и разделяет ее на две зеркальные половины, которые совпадают при отражении.

Диагональная ось симметрии проходит через центр фигуры и делит ее на две симметричные половины, которые являются зеркальными отражениями друг друга относительно этой оси.

Некоторые примеры фигур с осью симметрии:

Фигура	Ось симметрии
Квадрат	Вертикальная и горизонтальная оси симметрии
Прямоугольник	Вертикальная и горизонтальная оси симметрии
Круг	Бесконечное количество диагональных осей симметрии
Равносторонний треугольник	Три диагональные оси симметрии

Симметричные функции

Формально, функция f(x1, x2, …, xn) называется симметричной, если для любой перестановки аргументов xi значение функции остается неизменным:

Перестановка аргументовЗначение функции

x1, x2, …, xn	f(x1, x2, …, xn)
x2, x1, …, xn	f(x2, x1, …, xn)
…	…
xn, xn-1, …, x1	f(xn, xn-1, …, x1)

Примером симметричной функции является функция суммы двух чисел. Независимо от порядка, в котором числа будут сложены, сумма останется неизменной.

Симметричные графики

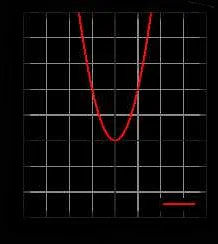
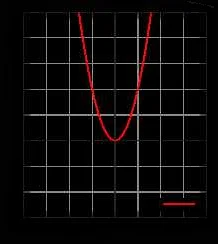
Симметричные графики могут быть использованы для отображения симметричных функций или отношений. Например, график функции f(x) = x^2 является симметричным относительно оси y, так как остается неизменным после отражения относительно этой оси. Это означает, что значение функции в точке a будет таким же, как и значение в точке -a.

Также симметричные графики могут быть использованы для отображения симметричных геометрических фигур, таких как круги или равносторонние треугольники. Например, график круга является симметричным относительно его центра, так как каждая точка графика находится на одинаковом расстоянии от центра.

Использование симметричных графиков может помочь визуализировать и понять симметричные свойства функций или геометрических фигур, что является важным инструментом в математике и других науках.

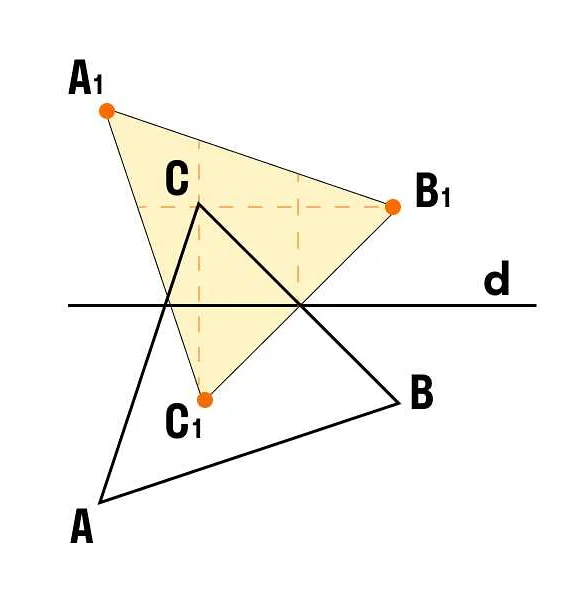
Симметричное отношение

Например, рассмотрим отношение «равенство» между двумя числами. Если число A равно числу B, то число B также равно числу A. Таким образом, отношение «равенство» является симметричным отношением.

Еще одним примером симметричного отношения является отношение «сходства» между геометрическими фигурами. Если фигура A похожа на фигуру B, то фигура B также похожа на фигуру A. Таким образом, отношение «сходства» также является симметричным отношением.

Симметричное отношение играет важную роль в математике и других науках, так как позволяет связывать элементы между собой и находить сходства и связи между ними.

Симметричные матрицы

Другими словами, симметричная матрица обладает свойством равенства элементов, расположенных на одинаковых позициях относительно главной диагонали. Например, элемент в строке i и столбце j будет равен элементу в строке j и столбце i.

Симметричные матрицы имеют ряд полезных свойств и применяются в различных областях математики и физики. Они являются основой для разработки алгоритмов и решений в линейной алгебре и теории графов.

Примеры симметричных матриц:

• Матрица, состоящая из одинаковых элементов по обеим сторонам главной диагонали.
• Матрица, которая является транспонированной самой себе.
• Матрица, полученная путем замены элементов симметрично относительно главной диагонали.

Симметричные матрицы являются важным объектом изучения в математике и находят применение в различных приложениях, включая графические модели, машинное обучение и анализ данных.

Примеры симметричности в природе и повседневной жизни

Одним из примеров симметрии в природе являются кристаллические структуры минералов. В кристаллах можно найти множество видов симметрии, таких как осевая симметрия, плоскостная симметрия и центральная симметрия. Они придают кристаллам эстетическую красоту и характеризуют их уникальную структуру.

Другим примером симметрии в природе являются лепестки цветов. Многие цветы имеют симметричные лепестки, которые располагаются вокруг центральной оси. Это создает гармоничный и красивый образ, который привлекает нас своей симметрией.

В повседневной жизни мы также сталкиваемся с симметричностью. Например, многие здания и сооружения имеют симметричную архитектуру. Симметричные фасады, окна и двери создают ощущение гармонии и баланса.

Симметрия также присутствует в мире моды. Многие симметричные узоры и орнаменты используются в дизайне одежды и аксессуаров, чтобы создать эстетически привлекательный образ.

В заключение, симметрия играет важную роль в природе и повседневной жизни. Она придает красоту и гармонию окружающему нас миру, делая его более приятным и привлекательным.

Вопрос-ответ:

Что такое симметричная фигура?

Симметричная фигура — это фигура, которая может быть разделена на две части таким образом, что они совпадают друг с другом при отражении в некоторой оси или плоскости. Примером симметричной фигуры может быть круг.

Какие бывают виды симметрии в математике?

В математике существуют три основных вида симметрии: симметрия относительно оси, симметрия относительно точки и симметрия относительно плоскости.

Как определить, является ли фигура симметричной?

Фигура является симметричной, если для каждой ее точки существует другая точка, симметричная относительно некоторой оси, точке или плоскости. Для проверки симметричности можно воспользоваться отражением фигуры относительно оси или плоскости и сравнением полученного изображения с исходной фигурой.

Какие есть примеры симметричных и несимметричных фигур?

Примерами симметричных фигур могут быть квадрат, круг, равносторонний треугольник. Несимметричными фигурами являются прямоугольник, произвольный треугольник, неравносторонний параллелограмм.

Какая роль симметрии в математике?

Симметрия играет важную роль в математике, поскольку она позволяет упрощать задачи и находить решения с помощью симметричных свойств фигур. Она также имеет широкое применение в других областях, таких как физика, химия, архитектура и искусство.

Что такое симметрия в математике?

Симметрия в математике — это свойство фигуры или объекта сохранять свою форму при некоторых преобразованиях. В математике симметрия может быть определена как равенство или совпадение относительно некоторой оси, плоскости или точки. Симметрия может быть геометрической (отражение относительно оси или плоскости) или алгебраической (равенство функций при замене переменных).

Какие примеры симметрии есть в математике?

В математике существует множество примеров симметрии. Одним из самых известных примеров является симметричный треугольник, у которого все три стороны и углы равны. Другим примером может быть симметричный круг, который при вращении на 180 градусов сохраняет свою форму. Также симметричной является функция y = x^2, которая симметрична относительно оси ординат.