Что такое равновеликие в математике
Содержимое
- 1 Что такое равновеликие в математике
- 1.1 Равновеликие в математике
- 1.2 Видео по теме:
- 1.3 Определение равновеликих в математике
- 1.4 Свойства равновеликих множеств
- 1.5 Примеры равновеликих множеств
- 1.6 Равновеликие множества и мощность
- 1.7 Равновеликие множества и операции над ними
- 1.8 Доказательство равновеликости множеств
- 1.9 Равновеликие множества и геометрия
- 1.10 Вопрос-ответ:
Равновеликие в математике — это геометрические фигуры, которые имеют одинаковую площадь, но могут иметь разные формы и размеры. Узнайте, как определить равновеликие фигуры и как они используются в решении задач.
В математике понятие равновеликих является одним из важных и широко используемых. Оно используется для определения равенства площадей или объемов различных геометрических фигур. Равновеликие фигуры имеют одинаковую площадь или объем, но могут иметь различную форму и размеры.
Определение равновеликих в математике можно сформулировать следующим образом: две геометрические фигуры называются равновеликими, если их площади или объемы равны. Это означает, что количество элементов, из которых состоят фигуры, может быть разным, но их общая площадь или объем будет одинаковыми.
Например, два треугольника с разными сторонами могут быть равновеликими, если их площади равны. То же самое относится и к прямоугольникам, кругам, шарикам и другим геометрическим фигурам. Важно отметить, что равновеликость не зависит от формы или размера фигур, а основывается исключительно на их площади или объеме.
Равновеликие фигуры играют важную роль в различных областях математики и ее применений, таких как геометрия, физика, экономика и другие. Они позволяют решать различные задачи, связанные с определением площади или объема фигур, а также делать выводы о их свойствах и взаимной равновеликости.
Равновеликие в математике
Примеры равновеликих множеств:
- Множество A = {1, 2, 3} и множество B = {a, b, c}. Оба множества содержат по 3 элемента, поэтому они равновеликие.
- Множество C = {4, 5, 6} и множество D = {x, y, z}. Оба множества содержат по 3 элемента, поэтому они также равновеликие.
- Множество E = {1, 2, 3, 4} и множество F = {a, b, c, d}. Оба множества содержат по 4 элемента, поэтому они равновеликие.
Важно отметить, что равновеликость множеств определяется только количеством их элементов, а не их содержимым. То есть, если два множества содержат одинаковое количество элементов, они будут равновеликими, независимо от того, какие элементы они содержат.
Видео по теме:
Определение равновеликих в математике
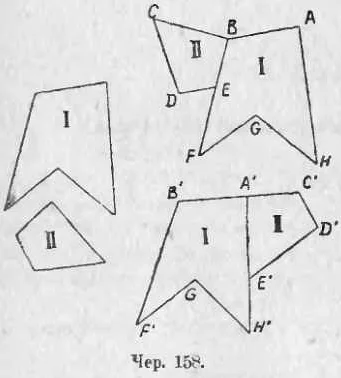
Для определения равновеликости двух фигур необходимо сравнить их площади. Площадь фигуры можно вычислить различными способами в зависимости от её формы. Например, для прямоугольника площадь вычисляется как произведение длины и ширины, а для круга — как произведение квадрата радиуса на число π.
Примеры равновеликих фигур:
Пример 1: Два прямоугольника со сторонами 3 и 4 могут быть равновеликими, если их стороны пропорциональны. Например, если стороны первого прямоугольника увеличить вдвое (6 и 8), то второй прямоугольник также будет иметь площадь 24 квадратных метра.
Пример 2: Два круга с радиусом 5 могут быть равновеликими, так как площадь круга вычисляется по формуле S = πr². Подставив значение радиуса 5 в формулу, получим площадь 25π для обоих кругов.
Таким образом, равновеликие фигуры имеют одинаковую площадь, независимо от формы и размера фигур.
Свойства равновеликих множеств
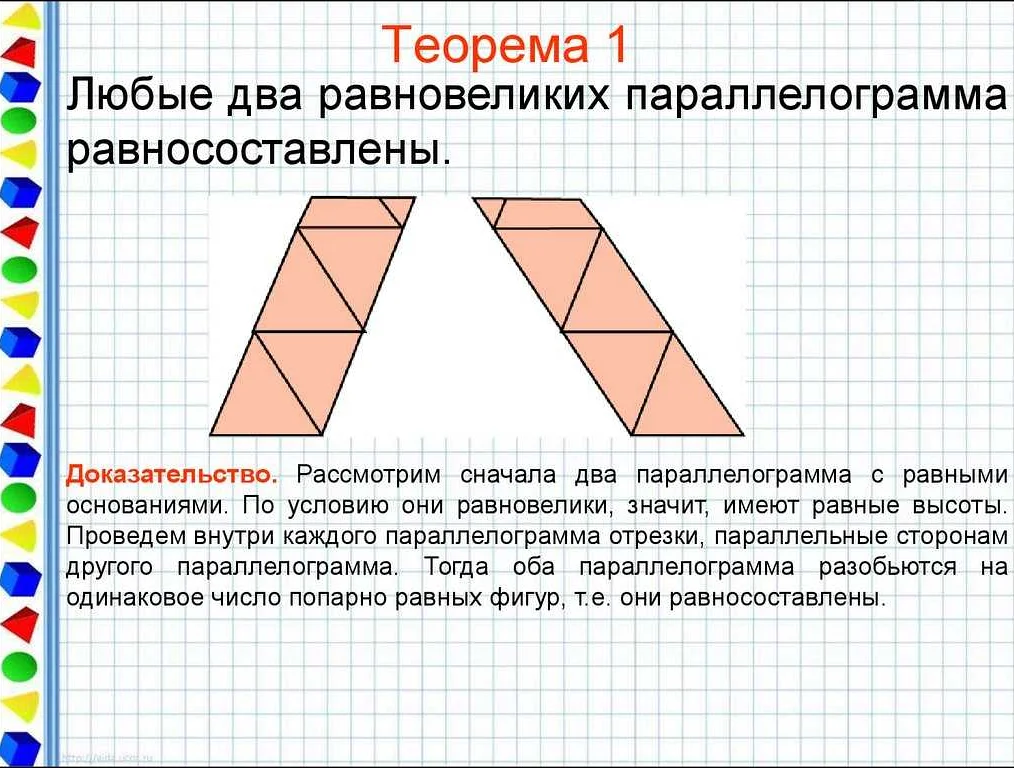
Равновеликие множества обладают рядом важных свойств, которые позволяют использовать их в математических рассуждениях и доказательствах. Ниже приведены основные свойства равновеликих множеств:
1. Рефлексивность: любое множество равновелико самому себе. То есть, для любого множества A справедливо A ~ A.
2. Симметричность: если множество A равновелико множеству B, то множество B равновелико множеству A. То есть, если A ~ B, то B ~ A.
3. Транзитивность: если множество A равновелико множеству B, а множество B равновелико множеству C, то множество A равновелико множеству C. То есть, если A ~ B и B ~ C, то A ~ C.
Эти свойства позволяют строить цепочки равновеликих множеств, что является важным инструментом в математических доказательствах. Кроме того, основные операции над множествами, такие как объединение и пересечение, сохраняют равновеликость множеств.
Например, если множество A равновелико множеству B, то их объединение A ∪ B также будет равновелико множеству B ∪ A. Аналогично, пересечение множеств A ∩ B будет равновелико пересечению множеств B ∩ A.
Таким образом, свойства равновеликих множеств позволяют работать с ними в математике, упрощая и обобщая различные задачи и доказательства.
Примеры равновеликих множеств
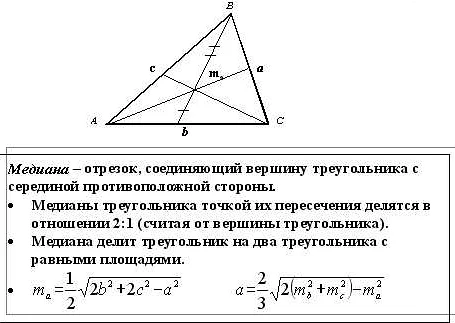
В математике существует множество примеров равновеликих множеств, когда два множества имеют одинаковую мощность, то есть содержат одинаковое количество элементов.
Некоторые примеры равновеликих множеств:
- Множество натуральных чисел и множество целых чисел. Оба множества содержат бесконечное количество элементов, поэтому они равновелики.
- Множество дробных чисел и множество вещественных чисел. Оба множества также содержат бесконечное количество элементов и равновелики между собой.
- Множество точек на отрезке [0, 1] и множество точек на прямой. Оба множества имеют континуальную мощность, то есть равновелики между собой.
- Множество букв русского алфавита и множество букв английского алфавита. Оба множества имеют конечное количество элементов и равновелики между собой.
Это лишь некоторые примеры равновеликих множеств. В математике существует бесконечное количество таких множеств, и изучение их свойств является важной частью теории множеств.
Равновеликие множества и мощность

В математике понятие равновеликих множеств относится к сравнению мощностей двух множеств, то есть к определению, содержат ли эти множества одинаковое количество элементов. Если два множества имеют одинаковую мощность, то они называются равновеликими.
Мощность множества обозначается символом |A|, где A — множество. Если множество A равновелико множеству B, то записывается |A| = |B|.
Примером равновеликих множеств может служить множество натуральных чисел и множество четных натуральных чисел. Оба этих множества содержат бесконечное количество элементов, поэтому они имеют одинаковую мощность и являются равновеликими.
Однако не все множества равновелики. Например, множество натуральных чисел и множество вещественных чисел имеют различную мощность. Мощность множества натуральных чисел считается счетной, а мощность множества вещественных чисел — континуальная, то есть больше счетной мощности.
Мощность множества может быть определена также с помощью кардинального числа. Кардинальное число определяет количество элементов в множестве и обозначается символом ℕ. Кардинальные числа используются для сравнения мощностей различных множеств.
Таким образом, равновеликие множества имеют одинаковую мощность и содержат одинаковое количество элементов. Они могут быть бесконечными или конечными, но их элементы соотносятся один к одному без остатка.
Равновеликие множества и операции над ними

Для определения равновеликости множеств используется понятие функции взаимно однозначного соответствия. Если между элементами двух множеств можно установить взаимно однозначное соответствие, то эти множества равновелики.
Операции над равновеликими множествами позволяют строить новые множества, которые также будут равновеликими исходным.
Объединение двух равновеликих множеств представляет собой операцию, результатом которой является множество, содержащее все элементы из обоих исходных множеств.
Пересечение двух равновеликих множеств представляет собой операцию, результатом которой является множество, содержащее только общие элементы из обоих исходных множеств.
Разность двух равновеликих множеств представляет собой операцию, результатом которой является множество, содержащее элементы только из первого множества, которые не принадлежат второму множеству.
Примеры равновеликих множеств и операций над ними могут быть представлены следующим образом:
Множество A = {1, 2, 3}
Множество B = {a, b, c}
Объединение множеств A и B: A ∪ B = {1, 2, 3, a, b, c}
Пересечение множеств A и B: A ∩ B = {} (пустое множество)
Разность множеств A и B: A \ B = {1, 2, 3}
Таким образом, равновеликие множества позволяют выполнять различные операции над элементами исходных множеств и получать новые равновеликие множества.
Доказательство равновеликости множеств
Для доказательства равновеликости множеств можно использовать различные методы, включая конструктивное доказательство и доказательство от противного.
Один из примеров доказательства равновеликости множеств – это доказательство равновеликости множеств натуральных чисел и четных натуральных чисел. Для этого можно построить соответствие между элементами этих множеств следующим образом:
- Каждому натуральному числу сопоставляем его удвоенное значение.
- Каждому четному натуральному числу сопоставляем его половину.
Такое соответствие является взаимно однозначным, так как каждому числу соответствует единственное другое число, и наоборот.
Таким образом, множество натуральных чисел и множество четных натуральных чисел являются равновеликими, так как мощности этих множеств совпадают.
Доказательство равновеликости множеств является важным инструментом в математике, так как позволяет установить равенство мощностей и сравнивать различные множества по их размеру.
Равновеликие множества и геометрия
В геометрии, равновеликие множества используются для сравнения геометрических фигур, таких как треугольники, прямоугольники, круги и др. Два множества геометрических фигур называются равновеликими, если они имеют одинаковую площадь или объем.
Например, рассмотрим два треугольника. Если у этих треугольников равны площади, то они считаются равновеликими. Аналогично, если у двух прямоугольников равны площади или у двух кругов равны площади, то они также считаются равновеликими.
Для определения равновеликости множеств геометрических фигур используются различные формулы и алгоритмы. Например, для прямоугольников можно использовать формулу площади S = a * b, где a и b — длины сторон прямоугольника.
Таблица ниже показывает примеры равновеликих множеств геометрических фигур:
ФигураПлощадь
| Треугольник ABC | 10 кв. ед. |
| Треугольник DEF | 10 кв. ед. |
| Прямоугольник PQRS | 20 кв. ед. |
| Прямоугольник XYZW | 20 кв. ед. |
| Круг O1 | π кв. ед. |
| Круг O2 | π кв. ед. |
В приведенной таблице видно, что треугольники ABC и DEF, прямоугольники PQRS и XYZW, а также круги O1 и O2 являются равновеликими, так как у них одинаковая площадь.
Вопрос-ответ:
Что такое равновеликие в математике?
В математике понятие равновеликих множеств означает, что два множества содержат одинаковое количество элементов. То есть они имеют одинаковую мощность.
Как определить, что два множества равновелики?
Для того чтобы определить, что два множества равновелики, необходимо построить взаимно однозначное соответствие между их элементами. Если такое соответствие существует, то множества равновелики.
Как можно представить равновеликие множества графически?
Равновеликие множества можно представить графически с помощью соответствующих диаграмм Эйлера. На диаграмме представлены два пересекающихся круга, каждый из которых представляет одно из множеств. Если круги имеют одинаковую площадь, то множества равновелики.
Приведите пример равновеликих множеств.
Примером равновеликих множеств может служить множество натуральных чисел и множество четных натуральных чисел. Оба множества содержат бесконечное количество элементов и могут быть сопоставлены друг другу взаимно однозначно.
Могут ли конечные множества быть равновеликими?
Да, конечные множества также могут быть равновеликими. Например, множество целых чисел от 1 до 5 и множество гласных букв русского алфавита содержат по 5 элементов и, следовательно, равновелики.
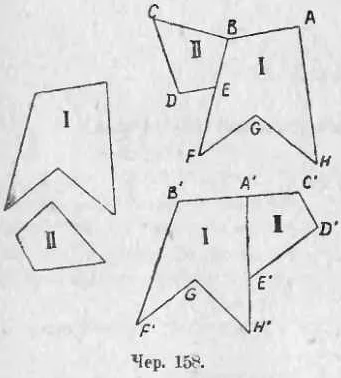



Очень интересная и познавательная статья! Раньше я часто слышала понятие «равновеликие», но не совсем понимала, что оно означает. Благодаря этой статье я наконец-то разобралась! Теперь я знаю, что равновеликие фигуры — это фигуры, которые могут быть разделены на конечное количество частей, каждая из которых подобна всей фигуре. В статье было дано несколько примеров, которые помогли мне лучше понять это понятие. Особенно запомнился пример с равновеликими треугольниками. Теперь, когда я вижу два треугольника, я могу проверить, равновеликие они или нет, исходя из условий, которые приведены в статье. Благодарю автора за четкое и понятное объяснение этой математической концепции! Теперь я чувствую себя немного увереннее в своих знаниях математики.