Что называется размещением в математике
Содержимое
- 1 Что называется размещением в математике
- 1.1 Размещение в математике: определение и примеры
- 1.2 Определение размещения в математике
- 1.3 Примеры размещения в математике
- 1.4 Размещение с повторением
- 1.5 Размещение без повторений
- 1.6 Формула для вычисления числа размещений
- 1.7 Практическое применение размещения
- 1.8 Размещение и комбинаторика
- 1.9 Выводы о размещении в математике
- 1.10 Вопрос-ответ:
- 1.10.0.1 Как определить понятие «размещение» в математике?
- 1.10.0.2 Какие примеры можно привести для понимания понятия «размещение»?
- 1.10.0.3 Чем размещение отличается от перестановки?
- 1.10.0.4 Какое математическое обозначение используется для размещений?
- 1.10.0.5 Какие свойства имеют размещения?
- 1.10.0.6 Что такое размещение в математике?
- 1.11 Видео по теме:
Размещение в математике – это процесс распределения объектов или элементов в определенном порядке или в соответствии с определенными правилами. Узнайте, как размещение используется для решения задач комбинаторики и перестановок в математике.
Размещение – это один из важных понятий в комбинаторике, которое широко применяется в математике и других науках. Размещение относится к так называемым комбинаторным задачам, которые изучают количество способов упорядоченного выбора элементов из заданного множества. В отличие от сочетаний и перестановок, размещения учитывают порядок элементов.
Формула для вычисления размещения из n элементов по k состоит из факториалов и обозначается как A(n, k). Если n и k – натуральные числа, то размещение вычисляется по формуле: A(n, k) = n! / (n — k)!. Здесь n! представляет собой факториал числа n, который равен произведению всех натуральных чисел от 1 до n, а (n — k)! – факториал разности n — k.
Например, если имеется 5 элементов (a, b, c, d, e), и нужно выбрать из них 3, то количество размещений будет равно A(5, 3) = 5! / (5 — 3)! = 5! / 2! = 5 * 4 * 3 = 60.
Размещения находят широкое применение в различных областях, таких как теория вероятностей, статистика, теория информации и другие. Они используются для определения вероятности наступления событий, расчета количества перестановок с повторениями, а также для решения различных задач, связанных с упорядочиванием элементов.
Размещение в математике: определение и примеры
Определение размещения можно выразить следующей формулой:
Ank = n! / (n — k)!
Где:
- Ank — количество размещений из n элементов по k;
- n — количество элементов в множестве;
- k — количество выбранных элементов для размещения;
- n! — факториал числа n, равный произведению всех натуральных чисел от 1 до n.
Например, предположим, что у нас есть множество {A, B, C}. Чтобы найти все размещения из этого множества по 2, мы используем формулу:
A32 = 3! / (3 — 2)! = 3! / 1! = 3
Таким образом, мы получаем 3 размещения: AB, AC и BC.
Размещения широко применяются в комбинаторике, криптографии, теории вероятностей и других областях математики. Они позволяют решать задачи выбора и упорядочивания элементов, что делает их полезными инструментами для анализа и моделирования реальных ситуаций.
Определение размещения в математике

Формула для вычисления размещения имеет вид:
| n | A | n | k | = | n! | / | (n — k)! |
Где n – количество элементов в множестве, а k – количество элементов, которые необходимо выбрать.
Например, пусть имеется множество из 4 элементов: {A, B, C, D}. Сколько разных трехэлементных подмножеств можно выбрать из данного множества?
Используя формулу размещения, получим:
| 4 | A | 4 | 3 | = | 4! | / | (4 — 3)! | = | 4 | × | 3 | × | 2 | × | 1 | = | 24 |
Таким образом, из данного множества можно выбрать и упорядочить 24 различных трехэлементных подмножества.
Примеры размещения в математике
Примером размещения может служить задача о выборе и расположении элементов в очереди. Предположим, что имеется 5 человек, которые желают занять очередь перед кассой. Сколькими способами можно разместить этих людей в очереди из 3 мест?
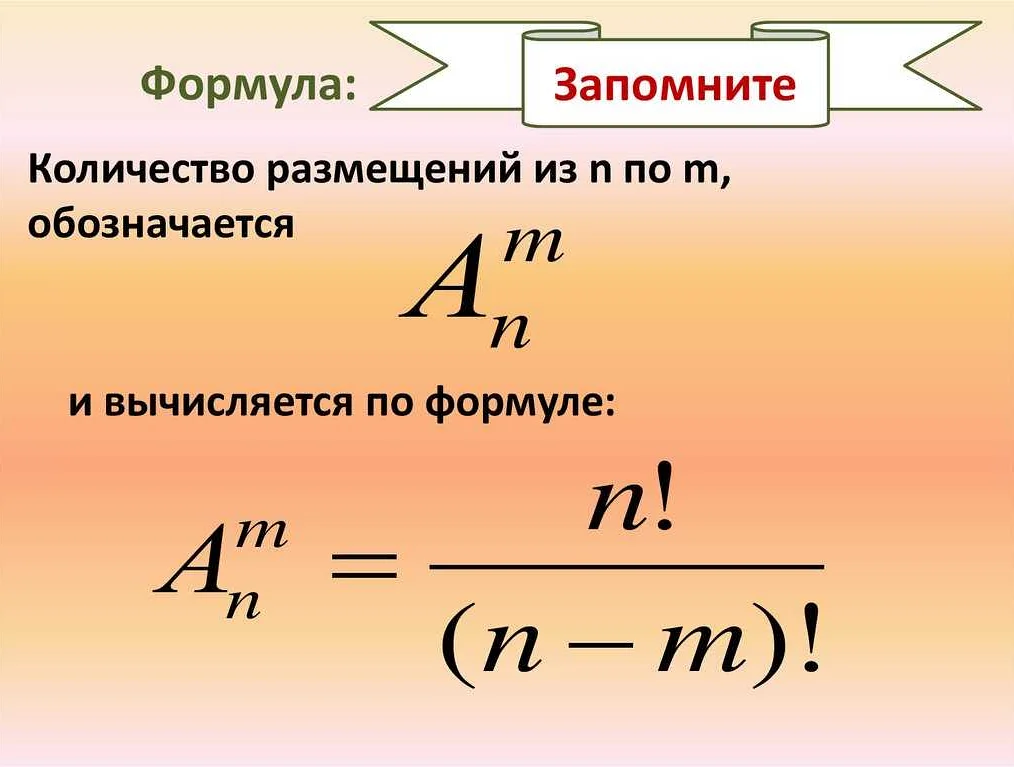
Для решения этой задачи применяют формулу для размещения без повторений:
Ank = n! / (n — k)!
Где Ank – количество размещений из n элементов по k местам.
В данном случае, n = 5 и k = 3, поэтому:
A53 = 5! / (5 — 3)! = 5! / 2! = 5 * 4 * 3 = 60
Таким образом, существует 60 различных способов разместить 5 человек в очереди из 3 мест.
Размещение с повторением
Формула для нахождения числа размещений с повторением имеет вид:
ФормулаОписание
| $$A_n^m = n^m$$ | Число размещений с повторением |
В этой формуле n — количество различных элементов для размещения, m — количество позиций для размещения элементов.
Примером размещения с повторением может служить расстановка книг на полке. Если у нас есть 3 различные книги и 5 полок, то с помощью размещения с повторением можно найти число способов расставить книги на полках.
В данном случае, число размещений с повторением будет равно:
$$A_5^3 = 5^3 = 125$$
Таким образом, есть 125 различных способов расставить 3 книги на 5 полках.
Размещение без повторений

Для вычисления количества размещений без повторений используется формула:
- n! / (m — n)!
Где n — количество элементов, участвующих в размещении, и m — количество доступных элементов.
Пример:
Предположим, у нас есть множество {A, B, C, D} и мы хотим выбрать 2 элемента из этого множества. Каково количество размещений без повторений?
Для решения этой задачи, мы можем использовать формулу размещения без повторений:
- 4! / (4 — 2)! = 4! / 2! = 4 * 3 = 12
Таким образом, количество размещений без повторений для данной задачи равно 12.
Формула для вычисления числа размещений
Размещение − это комбинаторный объект, в котором важна последовательность элементов. Формула для вычисления числа размещений из n элементов по k элементов определяется следующим образом:
Формула:
Ank = n! / (n — k)!
В данной формуле н! обозначает факториал числа n, которое равно произведению всех натуральных чисел от 1 до n:
n! = n * (n — 1) * (n — 2) * … * 3 * 2 * 1
Число размещений позволяет определить количество способов выбрать и расположить k элементов из n, причем каждый элемент может быть выбран только один раз и имеет значение его позиции в последовательности.
Например, пусть имеется набор из 5 элементов (A, B, C, D, E). Если необходимо выбрать и расположить 3 элемента из этого набора, то число размещений будет:
A53 = 5! / (5 — 3)! = 5! / 2! = 5 * 4 * 3 = 60
Таким образом, существует 60 различных способов выбрать и расположить 3 элемента из набора из 5 элементов.
Практическое применение размещения

1. Комбинаторика: Размещение используется для решения задач комбинаторного анализа, например, для определения количества способов выбрать и расположить элементы из заданного множества.
2. Теория вероятностей: Размещение помогает в вычислении вероятностей различных событий, основываясь на количестве способов размещения элементов в выборке.
3. Криптография: Размещение используется в криптографии для создания криптографических ключей и алгоритмов шифрования.
4. Маркетинг и реклама: Размещение играет важную роль в определении оптимального размещения рекламы, маркетинговых материалов и товаров на полках магазинов.
5. Информационные технологии: Размещение используется в алгоритмах сжатия данных, веб-разработке, распределении ресурсов и оптимизации производительности систем.
Все эти примеры демонстрируют важность и универсальность понятия размещения в различных областях науки и практике.
Размещение и комбинаторика
В комбинаторике размещение обозначается как Ank, где n — количество объектов, а k — количество позиций, в которых эти объекты могут быть размещены.
Для примера рассмотрим размещение пяти различных шаров в трех различных ящиках. В данном случае n = 5 (пять шаров) и k = 3 (три ящика). Каждый шар может быть размещен только в одном из трех ящиков.
Чтобы найти количество размещений, мы можем использовать формулу для размещения:
- Ank = n! / (n-k)!
- A53 = 5! / (5-3)! = 5! / 2! = 5 * 4 * 3 = 60
Таким образом, количество различных способов разместить пять шаров в трех ящиках равно 60.
Размещение является важным понятием в комбинаторике и находит применение в различных областях математики, таких как теория вероятностей, криптография и теория кодирования. Оно позволяет решать задачи, связанные с распределением объектов и определением количества возможных вариантов.
Выводы о размещении в математике
Основные выводы о размещении в математике:
- Размещение отличается от сочетания тем, что в размещении учитывается порядок элементов, а в сочетании — нет.
- Количество размещений можно рассчитать с помощью формулы размещений без повторений: Ank = n!/(n-k)!, где n — количество элементов в множестве, k — количество выбираемых элементов.
- Если в множестве есть повторяющиеся элементы, то используется формула размещений с повторениями: Ank/n1! * n2! * … * nk!, где n1, n2, …, nk — количество повторений каждого элемента.
- Размещение может быть полным, когда все элементы множества размещаются, или неполным, когда некоторые элементы остаются не размещенными.
- Размещение имеет широкое применение в различных областях, таких как комбинаторика, теория вероятности, статистика, теория игр и другие.
Выводы о размещении в математике позволяют нам лучше понять и использовать этот комбинаторный объект для решения различных задач и проблем в математике и других областях науки.
Вопрос-ответ:
Как определить понятие «размещение» в математике?
Размещение в математике — это комбинаторный объект, который представляет собой упорядоченную выборку элементов из заданного множества. При размещении порядок выбранных элементов имеет значение, то есть размещения, отличающиеся только порядком элементов, считаются разными.
Какие примеры можно привести для понимания понятия «размещение»?
Примеры размещений можно найти в повседневной жизни. Например, при выборе команды из группы людей для выполнения определенной задачи, можно рассмотреть размещение, где каждый член группы выполняет свою роль в определенной последовательности. Еще один пример — размещение букв в слове. При размещении букв в слове, изменение порядка букв приводит к образованию нового слова.
Чем размещение отличается от перестановки?
Размещение и перестановка являются связанными понятиями, но имеют некоторые различия. В перестановке порядок элементов имеет ключевое значение, и все элементы должны быть использованы. В размещении порядок также имеет значение, но не все элементы обязательно должны быть использованы.
Какое математическое обозначение используется для размещений?
Для обозначения размещений используется символ «A». Размещение из «n» элементов по «k» — это «n» взятое «k» размещение, и обозначается как A(n, k). Это число можно вычислить по формуле: A(n, k) = n! / (n-k)!, где «!» означает факториал числа.
Какие свойства имеют размещения?
У размещений есть несколько свойств. Во-первых, количество размещений зависит от числа элементов и количества выбираемых позиций. Во-вторых, при размещении каждый элемент может быть использован только один раз. В-третьих, порядок выбранных элементов имеет значение при размещении.
Что такое размещение в математике?
Размещение в математике — это комбинаторный объект, который позволяет определить количество способов выбрать и расположить определенное количество элементов из заданного множества в определенном порядке. Оно обозначается как A(n, k), где n — общее количество элементов, а k — количество выбираемых элементов.


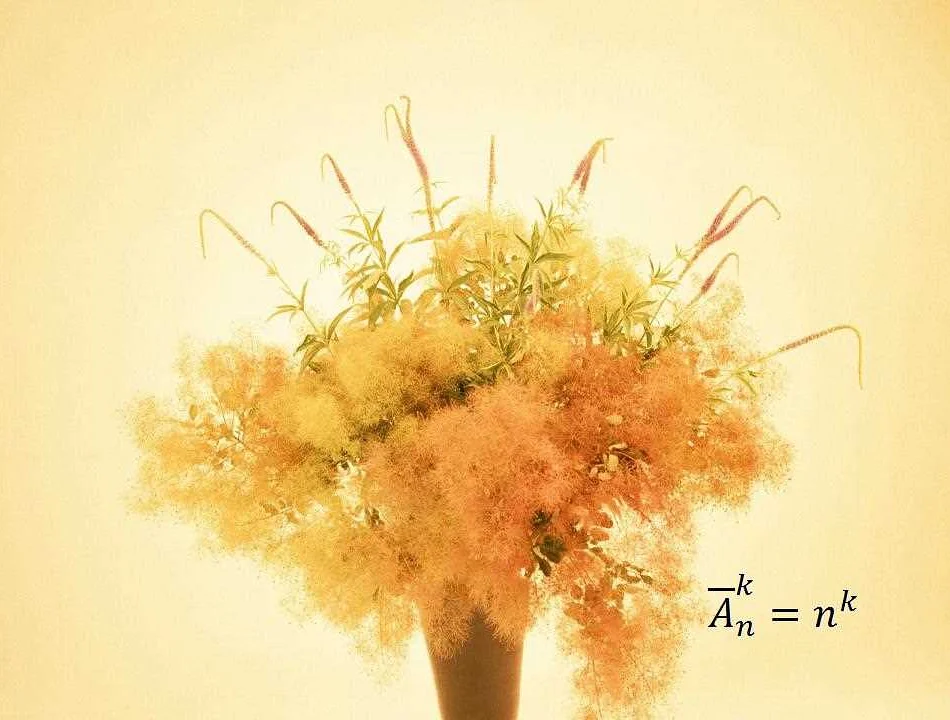


Математика всегда была для меня сложным предметом, но я всегда стремлюсь понять ее основы. Одним из таких основных понятий является размещение. Что же это такое? Размещение — это комбинаторный объект, который определяет, сколькими способами можно выбрать и расположить элементы в определенном порядке. Например, представим, что у меня есть 4 различных марки машин, и я хочу выбрать их и расположить в определенном порядке на полке. Сколько вариантов у меня есть? Ну, первую марку я могу выбрать из 4 вариантов, вторую — из 3, третью — из 2, и оставшуюся — из 1. Всего у меня получается 4*3*2*1 = 24 способа размещения марок машин на полке. Таким образом, размещение — это способ подсчета всех возможных комбинаций элементов в определенном порядке. Оно находит свое применение в различных областях, таких как теория вероятностей, комбинаторика, а также в решении задач на расстановку объектов. Я не всегда понимаю все тонкости математических терминов, но понимание размещений помогает мне лучше разобраться в задачах и находить решения.
Статья очень понятно объяснила, что такое размещение в математике. Я давно интересуюсь этой наукой, и такие подробности всегда приятно узнавать. Понятно, что размещение — это упорядоченное расположение объектов. Например, в статье был приведен пример с размещением книг на полке. Мне понравилось, как автор пошагово объяснил процесс и формулу для вычисления числа размещений. Теперь я точно знаю, как применить эту формулу в практических задачах. Статья была написана простым и доступным языком, и я с удовольствием прочитал ее до конца. Теперь у меня есть более глубокое понимание темы размещения в математике. Спасибо автору за ясное и понятное объяснение!