Что такое решето в математике

Решето в математике — это алгоритмический метод, позволяющий найти и выделить все простые числа из заданного диапазона. Узнайте, как работает решето и как оно применяется в различных задачах и алгоритмах.

Решето – это важный инструмент в математике, который применяется для отбора простых чисел из заданного диапазона. Оно основано на принципе исключения: сначала все числа рассматриваются как потенциально простые, а затем исключаются все числа, которые являются кратными другим числам. В результате остаются только простые числа.

Применение решета в математике широко распространено. Оно используется для решения различных задач, связанных с числами. Например, с помощью решета можно найти все простые числа в заданном диапазоне, определить, является ли заданное число простым или составным, а также факторизовать составное число на простые множители.

Решето Эратосфена – одно из наиболее известных и простых в использовании решет. Оно было разработано древнегреческим математиком Эратосфеном III века до н. э. и до сих пор широко применяется.

Использование решета позволяет значительно ускорить процесс поиска простых чисел. Благодаря его эффективности и простоте, решето находит свое применение не только в математике, но и в других областях, таких как криптография, теория чисел и компьютерные науки.

Решето в математике: определение и применение

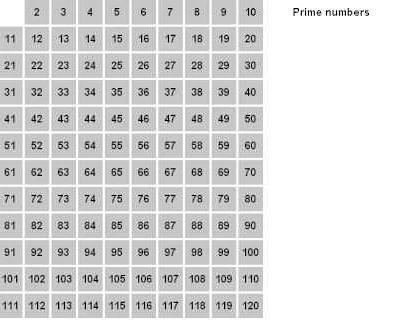
Процесс решета начинается с создания списка чисел от 2 до заданного максимального значения. Затем, начиная с 2, каждое число в списке проверяется на наличие делителей. Если число имеет делитель, оно удаляется из списка. Если число не имеет делителей, оно считается простым и оставляется в списке.

Применение решета в математике весьма широко. С его помощью можно эффективно находить все простые числа в заданном диапазоне. Это полезно при решении различных задач, например, при проверке числа на простоту или при нахождении наименьшего общего кратного двух чисел.

Решето Эратосфена является одним из самых известных примеров решета в математике. Оно было разработано древнегреческим математиком Эратосфеном и позволяет находить все простые числа в заданном диапазоне с использованием таблицы и шагового процесса удаления чисел.

Вывод: Решето в математике — это мощный инструмент, который позволяет находить все простые числа в заданном диапазоне. Оно имеет широкое применение в решении различных задач, связанных с простыми числами и их свойствами.

Что такое решето

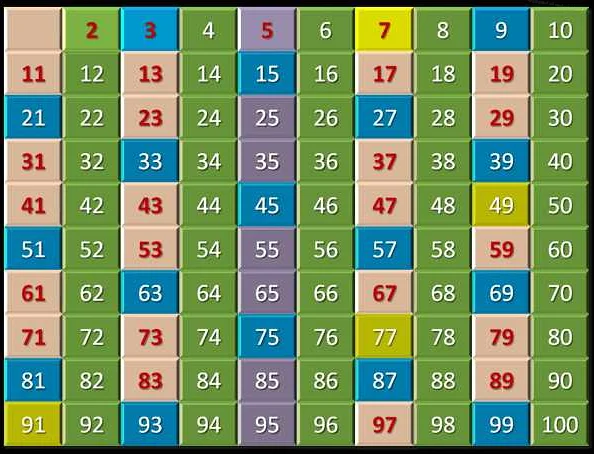
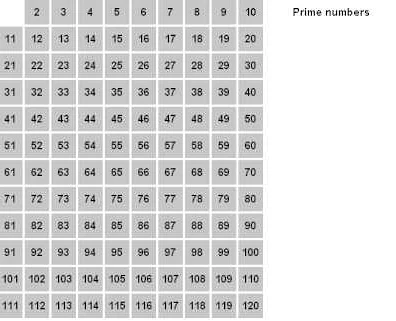
Простые числа — это числа, которые имеют только два делителя: 1 и само число. Например, 2, 3, 5, 7, 11 и т.д. являются простыми числами. Нахождение простых чисел имеет большое значение в различных областях математики и информатики.

Решето Эратосфена — один из наиболее известных и эффективных способов нахождения простых чисел. Оно основано на следующем алгоритме:

1. Создаем список чисел от 2 до заданного верхнего предела.
2. Начиная с числа 2, помечаем все его кратные числа в списке как составные числа.
3. Переходим к следующему непомеченному числу и повторяем процесс.
4. Повторяем шаг 3, пока не достигнем предела.

На выходе получаем список всех простых чисел в заданном диапазоне.

Решето также может использоваться для решения других задач, таких как нахождение наименьшего общего кратного или проверка числа на простоту.

Важно помнить, что решето является эффективным методом для нахождения простых чисел, особенно при работе с большими диапазонами чисел.

Принцип работы решета

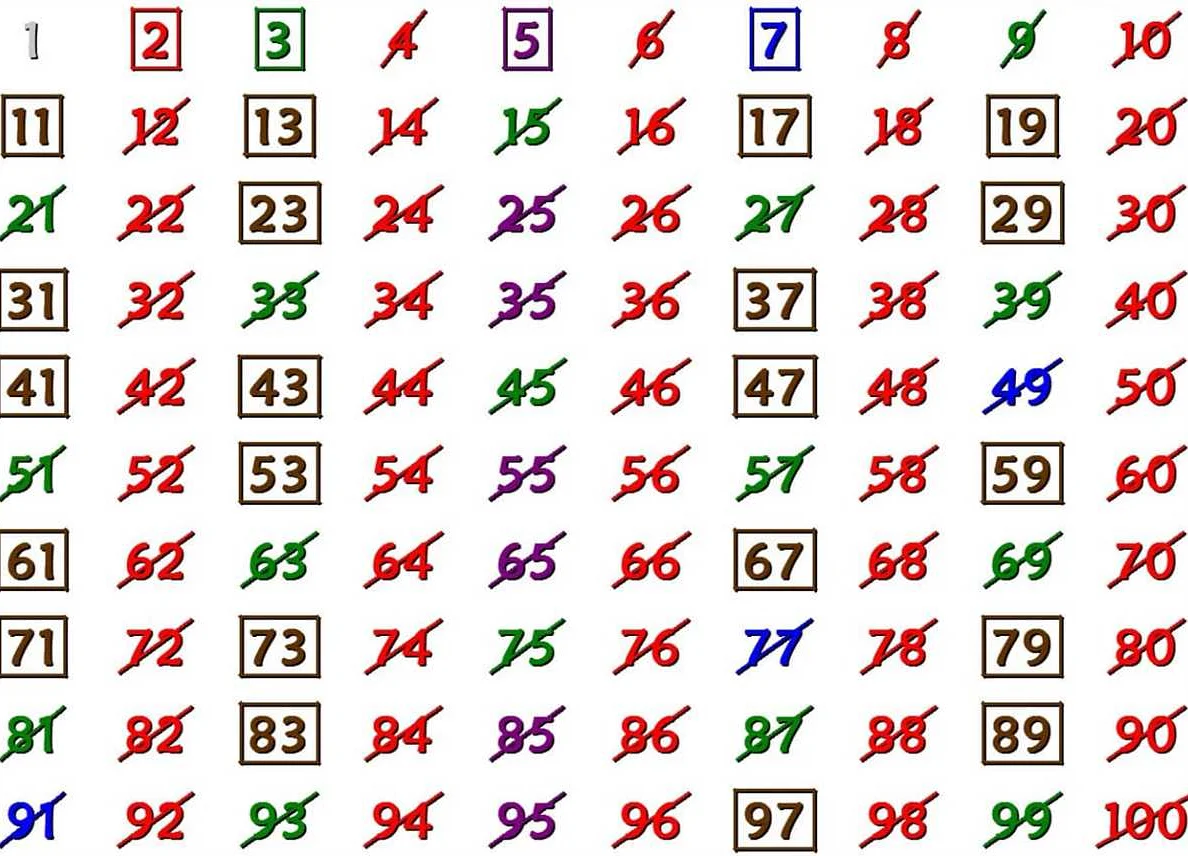
Процесс работы решета начинается с создания списка чисел от 2 до заданного верхнего предела. Затем, начиная с первого числа в списке, все его кратные числа помечаются как составные.

Далее, рассматривается следующее непомеченное число, которое не было исключено в предыдущих итерациях. Если оно не помечено как составное, то оно считается простым и все его кратные числа также помечаются.

Процесс повторяется, пока не будут рассмотрены все числа в списке. В результате, останутся только простые числа, которые не были помечены как составные. Эти числа и являются простыми числами в заданном интервале.

Принцип работы решета позволяет быстро и эффективно находить простые числа. Он широко применяется в различных областях математики и информатики, например, в криптографии и алгоритмах поиска простых чисел.

История решета

Идея решета в математике возникла еще в древней Греции. Однако первые упоминания о нем встречаются в работах греческого математика Эратосфена, жившего в III веке до нашей эры.

Эратосфен сформулировал теорему о решете, которая гласит, что любое число больше 1 можно представить в виде произведения простых чисел. Он также предложил способ нахождения всех простых чисел до заданного числа, который стал известен как «решето Эратосфена».

Решето Эратосфена – это алгоритм поиска всех простых чисел до заданного числа. Оно основано на идее постепенного вычеркивания кратных чисел. Процесс начинается с числа 2, которое считается первым простым числом. Затем все числа, кратные 2, вычеркиваются. Затем выбирается следующее не вычеркнутое число (3) и также вычеркиваются все его кратные. Процесс продолжается до тех пор, пока не будут вычеркнуты все числа до заданного числа.

Решето Эратосфена стало важным инструментом в математике и нашло применение в различных областях, например, в криптографии и алгоритмах поиска простых чисел. С течением времени были разработаны различные модификации решета, которые позволяют эффективно находить простые числа в больших интервалах.

Практическое применение решета

Решето Эратосфена, изначально разработанное греческим математиком Эратосфеном, находит широкое применение в современной математике и информатике.

Одним из практических применений решета является нахождение всех простых чисел в заданном диапазоне. Это может быть полезно, например, при проверке чисел на простоту или при генерации больших простых чисел для криптографических целей.

Еще одним применением решета является факторизация чисел. Решето может использоваться для разложения числа на простые множители, что может помочь в решении различных математических задач и задач из области криптографии.

Решето также может быть использовано для определения числа делителей у числа. Путем многократного применения решета и подсчета числа простых множителей можно определить количество делителей у заданного числа.

В информатике решето Эратосфена используется для решения различных задач, связанных с поиском простых чисел. Например, оно может быть использовано для определения простых чисел в заданном диапазоне или для проверки чисел на простоту в алгоритмах и программных решениях.

В целом, решето Эратосфена является мощным инструментом в математике и информатике, который находит широкое применение в различных областях. Его эффективность и простота использования делают его незаменимым инструментом для решения различных задач и проблем.

Решето в теории чисел

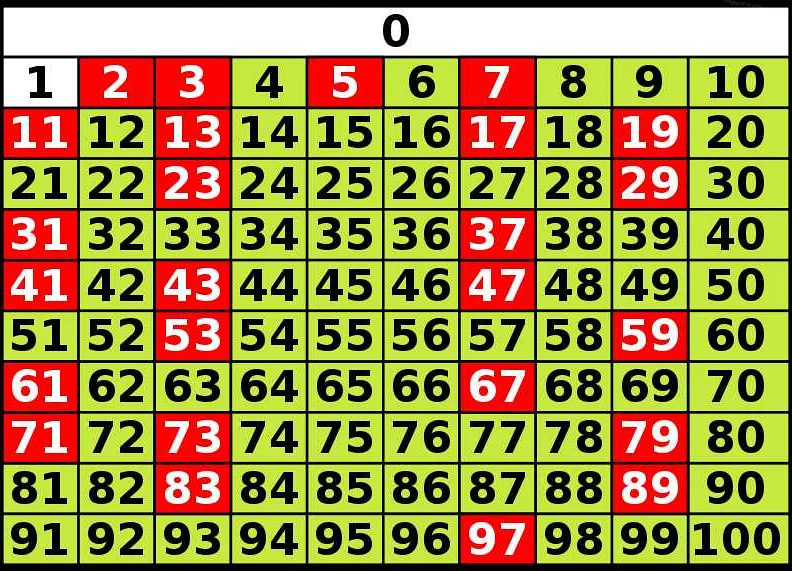
Простым числом называется натуральное число, большее единицы, которое делится без остатка только на единицу и само на себя. Решето позволяет найти все простые числа в заданном диапазоне, что является основой для многих задач в теории чисел, криптографии и других областях математики.

Решето Эратосфена является самым известным примером решета в теории чисел. Оно работает следующим образом:

1. Создаем список чисел от 2 до заданного верхнего предела.
2. Начиная с первого числа в списке (2), помечаем все его кратные числа как составные.
3. Переходим к следующему непомеченному числу и повторяем шаг 2.
4. Повторяем шаги 2-3, пока не достигнем верхнего предела.

В результате работы решета Эратосфена все помеченные числа будут составными, а непомеченные – простыми. Таким образом, мы можем получить все простые числа в заданном диапазоне.

Применение решета в теории чисел широко распространено. Оно используется для нахождения простых чисел для шифрования, проверки чисел на простоту, поиска делителей числа и многих других задач.

Решето Эратосфена

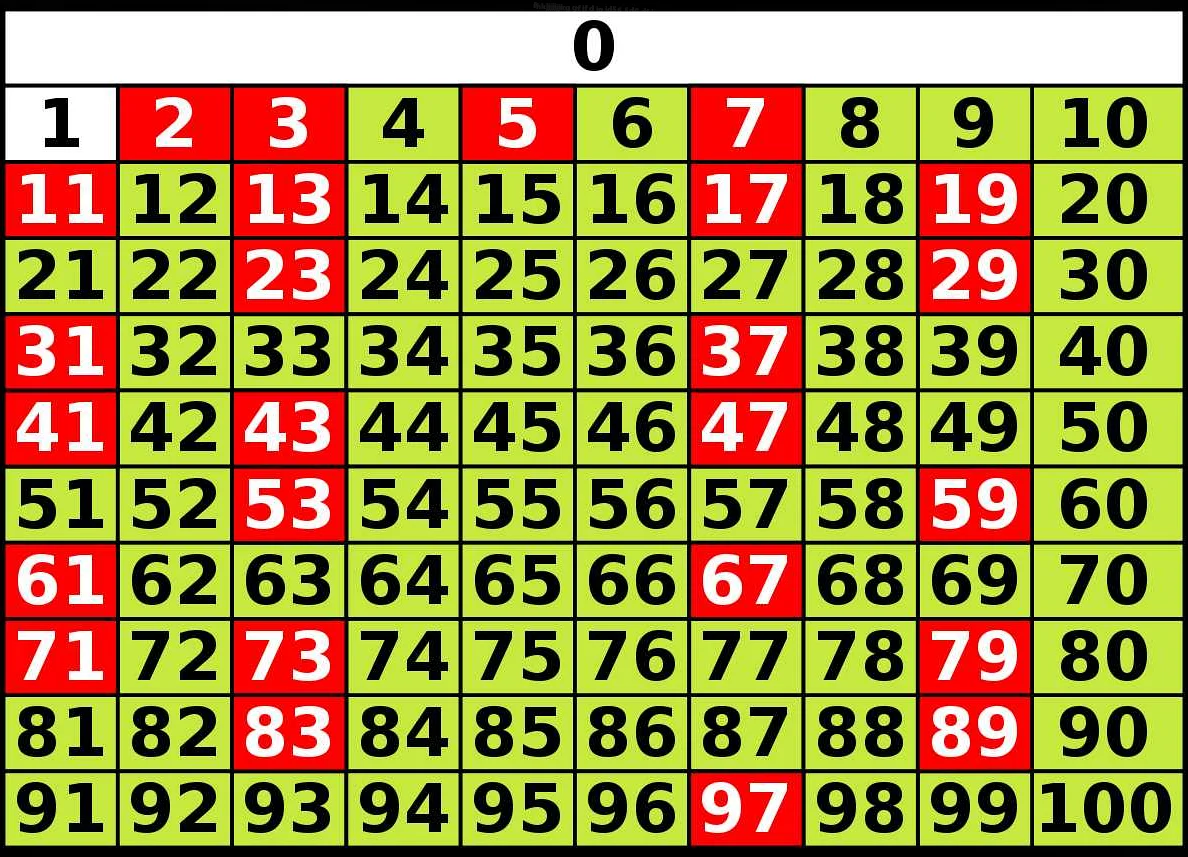
Основная идея решета Эратосфена заключается в том, чтобы последовательно отсеивать составные числа и оставлять только простые. Алгоритм начинается с создания списка всех чисел в заданном диапазоне, затем по очереди исключаются числа, кратные другим числам. В результате остаются только простые числа.

Процесс работы решета Эратосфена можно представить в виде следующих шагов:

1. Создать список чисел от 2 до заданного верхнего предела.
2. Начиная с числа 2, отметить все его кратные числа как составные.
3. Перейти к следующему неотмеченному числу и повторить предыдущий шаг.
4. Повторять шаги 2 и 3, пока не будут отмечены все числа в списке.
5. Оставить только неотмеченные числа в списке — это будут простые числа.

После выполнения алгоритма решета Эратосфена можно легко найти все простые числа в заданном диапазоне. Это особенно полезно при работе с большими наборами данных или при необходимости быстро определить простое число.

Алгоритмы поиска простых чисел с использованием решета

Алгоритм основан на следующем принципе: сначала создается список всех чисел от 2 до заданного числа N. Затем начиная с числа 2, все его кратные числа вычеркиваются из списка. Затем переходим к следующему не вычеркнутому числу и повторяем процесс, пока не достигнем числа N. В результате, все не вычеркнутые числа в списке являются простыми.

Более формально, алгоритм можно описать следующим образом:

1. Создать список чисел от 2 до N.
2. Пометить число 2 как простое.
3. Начиная с числа 2, вычеркнуть из списка все его кратные числа.
4. Перейти к следующему не вычеркнутому числу и пометить его как простое.
5. Повторять шаги 3-4, пока не достигнем числа N.

Алгоритм решета Эратосфена имеет временную сложность O(n log log n), что делает его очень эффективным для поиска простых чисел. Он также позволяет генерировать все простые числа до заданного числа N.

Другими популярными алгоритмами поиска простых чисел с использованием решета являются решето Сундарама и решето Аткина. Они основаны на том же принципе, но имеют некоторые отличия в реализации.

В заключение, алгоритмы поиска простых чисел с использованием решета являются эффективными и широко используются в математике и информатике. Они позволяют быстро находить простые числа и решать множество задач, связанных с этой темой.

Вопрос-ответ:

Что такое решето в математике?

Решето – это математический инструмент, который используется для нахождения всех простых чисел до заданного числа.

Как работает решето?

Решето работает по следующему принципу: сначала создается список всех чисел от 2 до заданного числа. Затем начиная с первого числа (2), все его кратные числа вычеркиваются из списка. Затем переходим к следующему невычеркнутому числу и повторяем процесс до тех пор, пока не пройдем все числа из списка. Оставшиеся невычеркнутые числа будут простыми.

Зачем нужно решето?

Решето нужно для нахождения всех простых чисел до заданного числа. Простые числа играют важную роль в математике и имеют множество приложений в различных областях, например, в криптографии, теории чисел, алгоритмах и др. Решето позволяет быстро и эффективно найти все простые числа в заданном диапазоне.

Как можно применить решето в практических задачах?

Применение решета Эратосфена в практических задачах может быть разнообразным. Например, оно может использоваться для проверки числа на простоту, для нахождения всех простых делителей числа, для генерации простых чисел в заданном диапазоне, для решения задач на простые числа в алгоритмах и т.д. Решето является мощным инструментом и находит применение во многих областях.

Какую историческую суть несет решето в математике?

Решето Эратосфена получило свое название в честь древнегреческого математика Эратосфена, который жил в III-II веках до нашей эры. Он разработал алгоритм решета для нахождения простых чисел. Использование решета было известно еще в Древней Греции, и с тех пор оно стало одним из фундаментальных инструментов в математике.

Что такое решето в математике?

Решето в математике — это инструмент, который используется для нахождения всех простых чисел в заданном диапазоне. Оно основано на методе исключения делителей и позволяет эффективно находить простые числа до заданного предела.

Как работает решето в математике?

Решето в математике работает по простому принципу исключения делителей. Сначала создается список чисел от 2 до заданного предела. Затем последовательно отсеиваются все числа, кратные 2, затем 3, затем 5 и так далее, пока не будут исключены все числа, кратные простым числам в заданном диапазоне. Оставшиеся числа в списке будут простыми числами.

Видео по теме: