Что такое простое число в математике

Простое число — это натуральное число, которое имеет ровно два делителя: единицу и само себя. Простые числа играют важную роль в математике и криптографии, их свойства и закономерности изучаются уже множество веков. Узнайте больше о простых числах и их значимости в математике.

Простое число – это натуральное число, которое имеет ровно два различных положительных делителя: единицу и само себя. Простые числа играют важную роль в математике и широко применяются в различных областях, включая криптографию и алгоритмы.

Простые числа имеют несколько ключевых свойств. Во-первых, они не могут быть получены путем перемножения других чисел, кроме как через единицу и само число. Во-вторых, любое число больше единицы может быть представлено в виде произведения простых чисел – это известно как теорема о разложении на простые множители.

Например, число 28 может быть разложено на простые множители: 28 = 2 * 2 * 7.

Простые числа обладают также другими интересными свойствами. Например, существует бесконечное количество простых чисел. Это было доказано древнегреческим математиком Евклидом более 2000 лет назад. Однако, задача поиска и классификации простых чисел остается актуальной и сложной для современной математики.

Простое число: определение, свойства, примеры

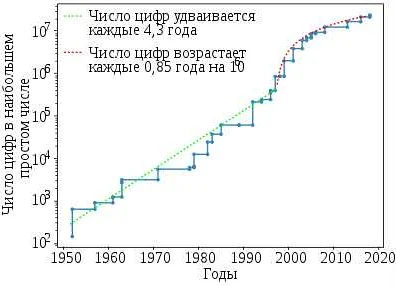
Простые числа являются важным объектом изучения в математике и широко применяются в различных областях, включая криптографию и теорию чисел.

Свойства простых чисел:

• Простые числа больше единицы.
• Простые числа не могут быть представлены в виде произведения других чисел, кроме себя и единицы.
• Простые числа расположены на числовой прямой без пропусков.
• Бесконечное количество простых чисел.

Примеры простых чисел:

Некоторые из наиболее известных простых чисел:

• 2
• 3
• 5
• 7
• 11
• 13

Простые числа играют важную роль в математике, и их свойства и характеристики продолжают изучаться и применяться для решения различных задач.

Что такое простое число

Простые числа играют важную роль в математике и имеют множество интересных свойств. Они являются основными строительными блоками для всех естественных чисел и используются в различных областях математики и криптографии.

Примерами простых чисел являются: 2, 3, 5, 7, 11, 13, 17, 19 и так далее. Количество простых чисел бесконечно, и они распределены по числовой прямой без определенной закономерности.

Заметим, что число 1 не является простым числом, так как оно имеет только один делитель.

Простые числа имеют важное место в теории чисел и используются в различных алгоритмах и задачах. Их свойства активно исследуются математиками и играют ключевую роль в развитии современной науки и технологий.

Определение простого числа

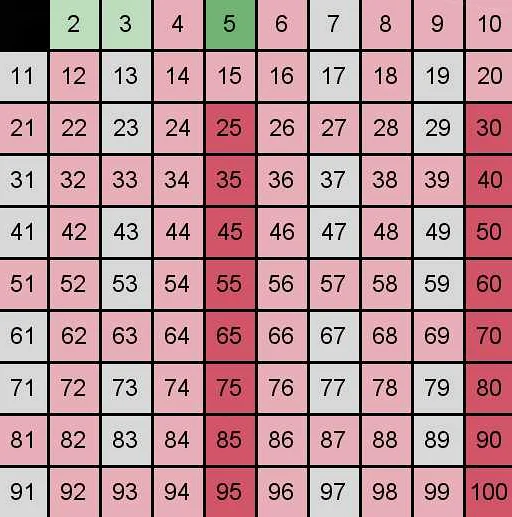
Простые числа являются основным строительным блоком для всех других чисел. Они обладают рядом уникальных свойств, которые делают их важными в математике и различных областях науки.

Например, числа 2, 3, 5, 7, 11, 13, 17 и 19 являются простыми числами, так как они не имеют других делителей, кроме 1 и самих себя.

Простые числа играют важную роль в различных областях, таких как криптография, теория чисел и алгоритмы. Их свойства и особенности изучаются математиками уже тысячелетиями и продолжают быть предметом активных исследований.

Свойства простых чисел

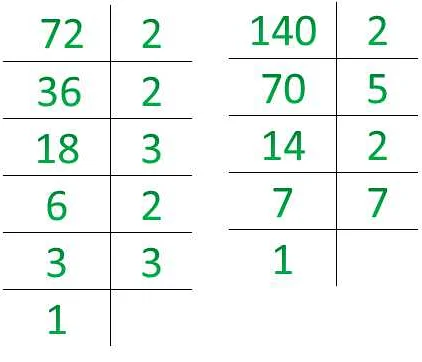
1. Простые числа имеют ровно два делителя: единицу и само число. Они не делятся на другие числа без остатка.

2. Простые числа больше единицы: ни одно число, кроме 1, не считается простым числом.

3. Простые числа не могут быть представлены в виде произведения других чисел: если число p является простым, то оно не может быть представлено в виде p = a * b, где a и b — другие числа.

4. Бесконечность простых чисел: существует бесконечное множество простых чисел. Никогда не сможет быть перечислено все простые числа.

5. Фундаментальная роль простых чисел в арифметике: простые числа играют важную роль в разложении чисел на простые множители и в решении различных задач в алгебре и числовой теории.

6. Взаимно простые числа: если два числа не имеют общих делителей, кроме 1, то они называются взаимно простыми. Простые числа являются взаимно простыми с любым другим числом, не являющимся их кратным.

7. Простые числа в криптографии: простые числа играют важную роль в криптографических алгоритмах, таких как алгоритм RSA, где безопасность основана на сложности факторизации больших чисел на простые множители.

Как определить простое число

Один из простых способов определения простого числа — это проверка его на делимость на все числа, меньшие его квадратного корня. Если число делится на какое-либо из этих чисел без остатка, то оно не является простым. Если же число не делится ни на одно из этих чисел, то оно является простым.

Например, для определения, является ли число 17 простым, проверим его на делимость на все числа от 2 до 4 (квадратный корень из 17 округленный в меньшую сторону).

ЧислоДелимость

2	Не делится
3	Не делится
4	Не делится

Таким образом, число 17 не делится на числа от 2 до 4 без остатка, следовательно, оно является простым числом.

Еще один известный алгоритм проверки числа на простоту — это алгоритм Эратосфена. Он основан на построении таблицы с числами от 2 до заданного числа и последовательном вычеркивании всех составных чисел. Если после завершения алгоритма число остается незачеркнутым, то оно является простым.

Возможно, существуют и другие методы определения простых чисел, но описанные выше методы являются наиболее распространенными и простыми в использовании.

Примеры простых чисел

Примеры простых чисел

2
3
5
7
11
13
17
19
23
29

Это всего лишь некоторые примеры простых чисел. В действительности, простых чисел бесконечное множество, и их можно найти в любом диапазоне чисел.

Простые числа в математике

Простые числа играют важную роль в теории чисел и имеют множество свойств и особенностей. Они являются «строительными блоками» для составных чисел, которые могут быть разложены на множители из простых чисел.

Примеры простых чисел включают: 2, 3, 5, 7, 11, 13, 17 и так далее. Существует бесконечное количество простых чисел, и их распределение в наборе натуральных чисел изучается в теории простых чисел.

Простые числа имеют множество интересных свойств и применений. Они используются в криптографии для шифрования информации, в алгоритмах проверки чисел на простоту и в других областях математики и информатики.

Видео по теме:

Вопрос-ответ:

Что такое простое число?

Простое число — это натуральное число больше единицы, которое имеет только два делителя: единицу и само себя. В простых числах нет других делителей.

Какие свойства имеют простые числа?

Простые числа обладают несколькими основными свойствами. Во-первых, любое натуральное число больше единицы может быть разложено на простые множители. Во-вторых, у простого числа нет других делителей, кроме единицы и самого себя. В-третьих, количество простых чисел бесконечно.

Можете привести примеры простых чисел?

Некоторые примеры простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23 и так далее. Все эти числа имеют только два делителя — единицу и само себя.

Какие методы существуют для определения простых чисел?

Для определения простых чисел существует несколько методов. Один из наиболее простых методов — это проверка делителей. Можно последовательно делить число на все числа, начиная от 2 и заканчивая корнем из этого числа. Если делитель найден, то число не является простым. Еще один метод — решето Эратосфена, которое позволяет найти все простые числа до заданного числа.

Какую роль играют простые числа в математике и криптографии?

Простые числа играют важную роль в математике и криптографии. Они используются для шифрования информации и создания защищенных протоколов. Например, в алгоритме RSA основным шагом является факторизация большого числа на простые множители. Также простые числа используются в различных математических доказательствах и теориях чисел.

Значение простых чисел

Одно из главных значений простых чисел заключается в их использовании в криптографии. Простые числа используются для создания шифров и обеспечения безопасности информации. Это связано с трудностью факторизации больших чисел, которые образованы произведением двух простых чисел.

Простые числа также используются для определения знака числа. Например, если число является простым, то его знак будет положительным. Если же число может быть разложено на простые множители, то его знак будет определен множителями.

Простые числа также встречаются в различных областях науки, включая физику, химию и биологию. Они используются для моделирования различных физических и химических процессов, а также для изучения генетической структуры организмов.

Простые числа также играют важную роль в различных алгоритмах и математических моделях. Они используются для оптимизации вычислений и упрощения сложных задач. Например, в алгоритме быстрого возведения в степень простые числа используются для разложения числа на множители и упрощения вычислений.

Таким образом, простые числа имеют большое значение в математике и науке в целом. Они являются основой для многих математических концепций и имеют широкий спектр применений в различных областях знания.

Применение простых чисел в науке и технологиях

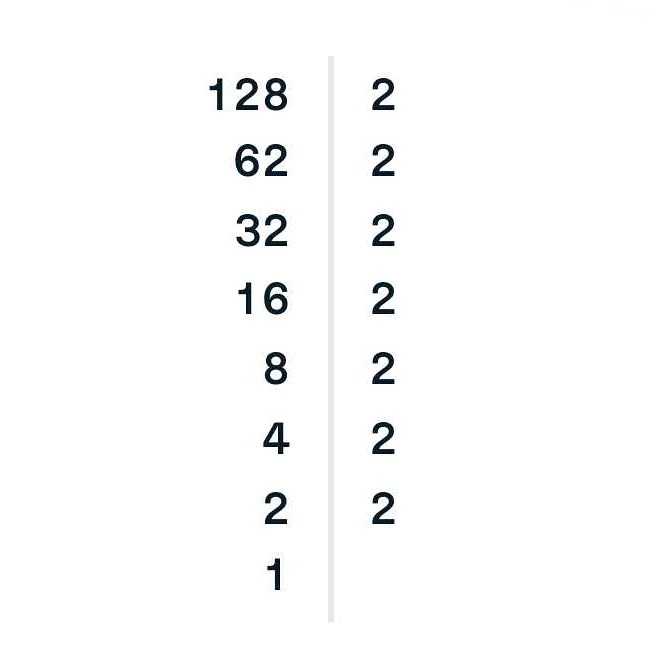
Одно из основных применений простых чисел – в криптографии. Криптография – это наука о защите информации от несанкционированного доступа. Простые числа используются в качестве ключей шифрования, которые обеспечивают безопасность передачи данных. Например, алгоритм RSA, который широко применяется в интернете для защиты конфиденциальности информации, основан на использовании простых чисел.

Простые числа также применяются в теории чисел и математической логике. Они играют важную роль в исследовании различных математических свойств и закономерностей. Например, простые числа используются в доказательствах теорем и в разработке новых математических концепций.

Одно из практических применений простых чисел – в информационных технологиях. Они используются в алгоритмах проверки целостности данных, хэширования, генерации случайных чисел и других задач. Простые числа обладают свойством сложности факторизации, что делает их надежными для ряда задач, связанных с обработкой информации.

Простые числа находят применение также в физике и инженерии. Они используются в моделировании физических процессов, в расчетах сложных систем и в разработке алгоритмов для оптимизации процессов. Простота простых чисел и их математические свойства помогают упростить и ускорить вычисления в различных областях науки и технологий.

Таким образом, простые числа являются неотъемлемой частью многих научных и технологических разработок. Их уникальные свойства и возможности находят применение в криптографии, математике, информационных технологиях, физике и других областях, способствуя развитию науки и техники в целом.