Что такое счастливое число в математике
Содержимое
- 1 Что такое счастливое число в математике
- 1.1 Определение счастливого числа
- 1.2 Ряд Фибоначчи и счастливые числа
- 1.3 Простые и составные счастливые числа
- 1.4 Сумма и произведение счастливых чисел
- 1.5 Счастливые числа и квадратные корни
- 1.6 Счастливые числа и десятичное представление
- 1.7 Счастливые числа и дзета-функция Римана
- 1.8 Вопрос-ответ:
- 1.9 Применение счастливых чисел в практике
- 1.10 Видео по теме:
Счастливое число в математике – это число, которое обладает особой энергией и связано с удачей и успехом. Узнайте, как определить счастливые числа и как они используются в различных областях жизни.
Счастливое число — это число, которое в специальном математическом эксперименте оказывается особенно «счастливым» или «удачным». Чаще всего этот эксперимент основан на манипуляциях с цифрами числа, таких как сложение, вычитание и возведение в квадрат.
Одним из известных методов определения счастливых чисел является процесс последовательного сложения цифр числа. Если после нескольких итераций сумма цифр равна 1, то число считается счастливым. В противном случае, если сумма цифр не равна 1 и не стабилизируется на каком-то другом числе, число считается несчастливым.
Счастливые числа имеют свои интересные свойства и встречаются в различных областях математики. Они имеют отношение к теории вероятностей, числовым системам, теории графов и другим математическим дисциплинам.
Например, счастливые числа могут быть использованы в задачах теории вероятностей для моделирования случайных процессов или генерации случайных чисел. Они также могут быть использованы в качестве ключей или значений в хэш-таблицах и других структурах данных.
Однако счастливые числа не являются редкостью или уникальным явлением. Напротив, счастливые числа встречаются в большом количестве и могут быть найдены в различных числовых последовательностях или рядах. Они продолжают привлекать внимание математиков и исследователей своими интересными свойствами и возможностями применения.
Определение счастливого числа
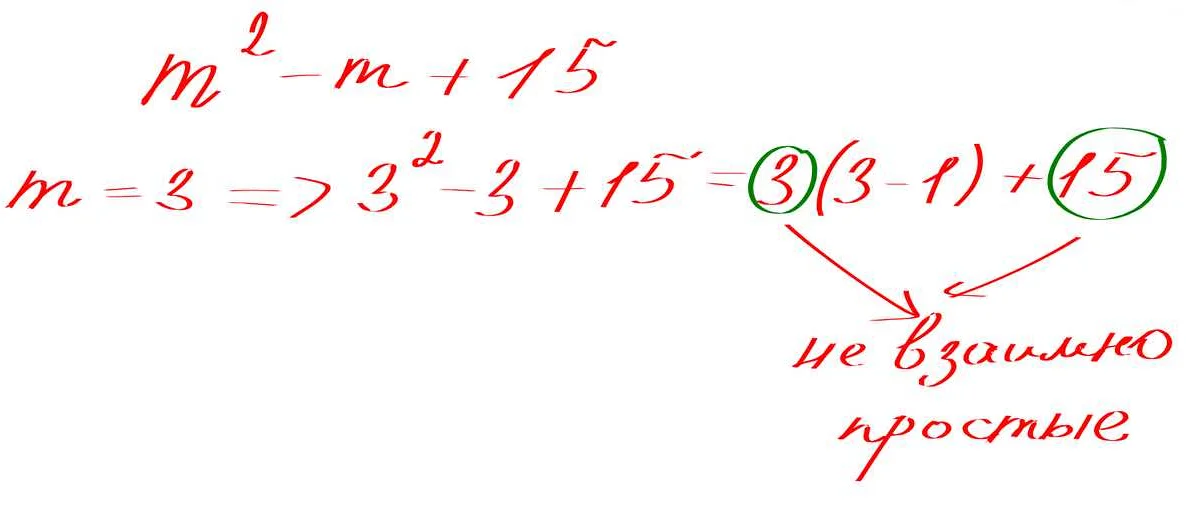
Для того чтобы определить, является ли число счастливым, необходимо взять исходное число и разделить его на цифры. Затем каждую цифру возвести в квадрат и сложить получившиеся результаты. Этот процесс необходимо повторять до тех пор, пока не будет получена конечная последовательность. Если в результате получится число единица, то исходное число является счастливым. В противном случае, если последовательность будет бесконечной или в ней будет содержаться число 4, то число считается несчастливым.
Например, рассмотрим число 19. Разделим его на цифры: 1 и 9. Затем возведем каждую цифру в квадрат и сложим результаты: 1^2 + 9^2 = 1 + 81 = 82. Повторим процесс для полученного числа: 8^2 + 2^2 = 64 + 4 = 68. И опять для полученного числа: 6^2 + 8^2 = 36 + 64 = 100. И, наконец, для числа 100: 1^2 + 0^2 + 0^2 = 1. В результате получилось число 1, что значит, что число 19 является счастливым.
Таким образом, счастливые числа обладают особым свойством, которое связано с их математической природой и результатом определенных операций.
Ряд Фибоначчи и счастливые числа

Счастливые числа — это числа, в последовательности цифр которых существует такое расположение, что сумма квадратов цифр равна 1. Например, число 7 является счастливым, так как 7^2 = 49, а 4^2 + 9^2 = 97, и 9^2 + 7^2 = 130. Поскольку сумма квадратов цифр числа 130 равна 10, а сумма квадратов цифр числа 10 равна 1, число 7 является счастливым.
Интересно отметить, что некоторые числа в ряду Фибоначчи также являются счастливыми. Например, число 13 в ряду Фибоначчи является счастливым, так как 1^2 + 3^2 = 10, а сумма квадратов цифр числа 10 равна 1.
Среди первых нескольких чисел в ряду Фибоначчи можно выделить также числа 1, 2 и 8, которые также являются счастливыми. Однако, не все числа в ряду Фибоначчи являются счастливыми, и такие числа становятся все более редкими с увеличением значения в ряду.
Интересно исследовать, какие еще числа в ряду Фибоначчи являются счастливыми и какие закономерности можно найти в их расположении и свойствах.
Простые и составные счастливые числа
Составные числа, в отличие от простых, имеют больше двух делителей. Например, число 4 является составным, так как имеет делители 1, 2 и 4.
Счастливые числа могут быть как простыми, так и составными. Например, число 7 — счастливое простое число, так как оно является простым числом и также удовлетворяет условию счастливого числа.
С другой стороны, число 14 является счастливым составным числом, так как оно имеет делители 1, 2, 7 и 14, и также удовлетворяет условию счастливого числа.
Таким образом, счастливые числа могут быть как простыми, так и составными, и это зависит от их делителей.
Сумма и произведение счастливых чисел
Сумма счастливых чисел может быть найдена путем сложения двух или более счастливых чисел. Например, если у нас есть счастливое число 7 и счастливое число 10, их сумма будет равна 17.
Произведение счастливых чисел может быть найдено путем умножения двух или более счастливых чисел. Например, если у нас есть счастливое число 3 и счастливое число 5, их произведение будет равно 15.
Сумма и произведение счастливых чисел могут иметь различные свойства и особенности. Например, сумма двух счастливых чисел не всегда будет счастливым числом, и произведение двух счастливых чисел также не всегда будет счастливым числом.
В общем случае, сумма и произведение счастливых чисел могут быть вычислены по обычным правилам математики, но они все равно остаются счастливыми числами и сохраняют свои особенности.
Счастливые числа и квадратные корни

Одной из интересных особенностей счастливых чисел является связь с квадратными корнями. Если взять счастливое число и вычислить квадратный корень из него, то получится число, которое также является счастливым.
Например, рассмотрим число 49. При сложении квадратов его цифр получим следующую цепочку: 4^2 + 9^2 = 16 + 81 = 97. Затем повторим процесс для числа 97: 9^2 + 7^2 = 81 + 49 = 130. Продолжим, пока не получим число 1: 1^2 + 3^2 + 0^2 = 1 + 9 + 0 = 10, 1^2 + 0^2 = 1.
Теперь вычислим квадратный корень из числа 49: √49 = 7. Заметим, что 7 является счастливым числом. Таким образом, существует связь между счастливыми числами и квадратными корнями.
Еще одним интересным фактом является то, что не все счастливые числа имеют квадратные корни. Например, число 13 является счастливым, но его квадратный корень не является целым числом.
Из этого следует, что связь между счастливыми числами и квадратными корнями не является единственной, но она является одной из интересных особенностей этих чисел.
Счастливые числа и десятичное представление
Для определения, является ли число счастливым, следует разделить его на две равные части, просуммировать цифры в каждой из них и сравнить полученные суммы. Если они равны, то число считается счастливым. Если нет, следует продолжать этот процесс до тех пор, пока не будет получен результат.
Счастливые числа обладают рядом интересных свойств. Например, сумма десятичных цифр счастливых чисел всегда равна 1, 7 или 9. Кроме того, если число является счастливым, то его квадрат также будет счастливым числом.
Счастливые числа и дзета-функция Римана

Дзета-функция Римана — это функция, определенная на комплексной плоскости и широко используемая в анализе и теории чисел. Она обозначается символом ζ(s) и определяется как сумма ряда:
ζ(s) = 1^(-s) + 2^(-s) + 3^(-s) + 4^(-s) + …
где s — комплексное число со значением Re(s) > 1, а ^ обозначает возведение в степень.
Дзета-функция Римана тесно связана с счастливыми числами. В частности, известно, что для действительных чисел s > 1 справедливо следующее утверждение: если ζ(s) не равна нулю, то все счастливые числа являются числами, принадлежащими области сходимости функции ζ(s).
Однако, неизвестно, обратное утверждение: существуют ли какие-либо счастливые числа, которые не являются числами, принадлежащими области сходимости функции ζ(s). Этот вопрос остается открытым и является предметом исследований в теории чисел.
Вопрос-ответ:
Что такое счастливое число?
Счастливое число в математике — это число, которое при последовательном сложении и квадрате цифр его десятичной записи в итоге приводит к числу 1. Например, число 7 является счастливым, так как при сложении и квадрате его цифры получается: 7 → 49 → 16 → 37 → 58 → 89 → 145 → 42 → 20 → 4 → 16 → 37 → 58 → 89 → 145 → 42 → 20 → 4 → … и так далее, но никогда не приводит к числу 1.
Какие свойства у счастливых чисел?
У счастливых чисел есть несколько интересных свойств. Во-первых, каждое счастливое число содержит только цифры 1 и 7. Во-вторых, если у нас есть счастливое число, то мы можем получить другое счастливое число, поменяв местами цифры 1 и 7. Например, если 7 — счастливое число, то 71 тоже будет счастливым числом. В-третьих, счастливые числа образуют последовательность: 7, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70 и так далее.
Является ли число 13 счастливым числом?
Да, число 13 является счастливым числом. При последовательных операциях сложения и квадратирования его цифр мы получаем: 13 → 10 → 1, что в итоге приводит к числу 1. Таким образом, 13 — счастливое число.
Можно ли сказать, что счастливые числа имеют какое-то специальное значение или силу?
Нет, счастливые числа в математике не имеют какого-то особого значения или силы. Они являются лишь интересным классом чисел, обладающих определенными свойствами при последовательных операциях сложения и квадратирования их цифр. Считается, что эти числа принесут удачу, но это скорее поверье и шутка, нежели научно доказанное утверждение.
Есть ли какие-то практические применения счастливых чисел?
Счастливые числа, в основном, представляют интерес с точки зрения теории чисел и математической развлекательности. Однако, в некоторых областях, например, в информационной безопасности, счастливые числа могут использоваться в качестве «случайных» чисел для генерации паролей или шифрования данных. Также, счастливые числа могут быть использованы в некоторых алгоритмах генетического программирования или при разработке игр, где требуется случайный выбор чисел.
Применение счастливых чисел в практике

Счастливые числа, несмотря на свою простоту, имеют множество практических применений:
- В финансах: счастливые числа используются в различных финансовых операциях, таких как расчеты процентов, прогнозирование изменений курсов валют или акций. Некоторые люди даже предпочитают выбирать счастливые числа для своих финансовых операций, надеясь на удачу.
- В графическом дизайне: счастливые числа могут использоваться при создании гармоничных композиций и баланса в дизайне. Они могут помочь создать эстетически приятные и привлекательные изображения и макеты.
- В играх: счастливые числа часто используются в различных играх, как символ удачи. Некоторые люди предпочитают выбирать счастливые числа при покупке лотерейных билетов или участии в азартных играх, надеясь на выигрыш.
- В программировании: счастливые числа могут использоваться в алгоритмах и программных кодах для генерации случайных чисел или создания различных математических вычислений.
- В личной жизни: некоторые люди считают, что счастливые числа могут приносить удачу и благополучие в личной жизни. Они могут использовать эти числа для выбора даты свадьбы, покупки недвижимости или других важных событий в их жизни.
В общем, счастливые числа могут играть не только математическую роль, но и иметь сильное влияние на нашу повседневную жизнь и принимаемые нами решения.
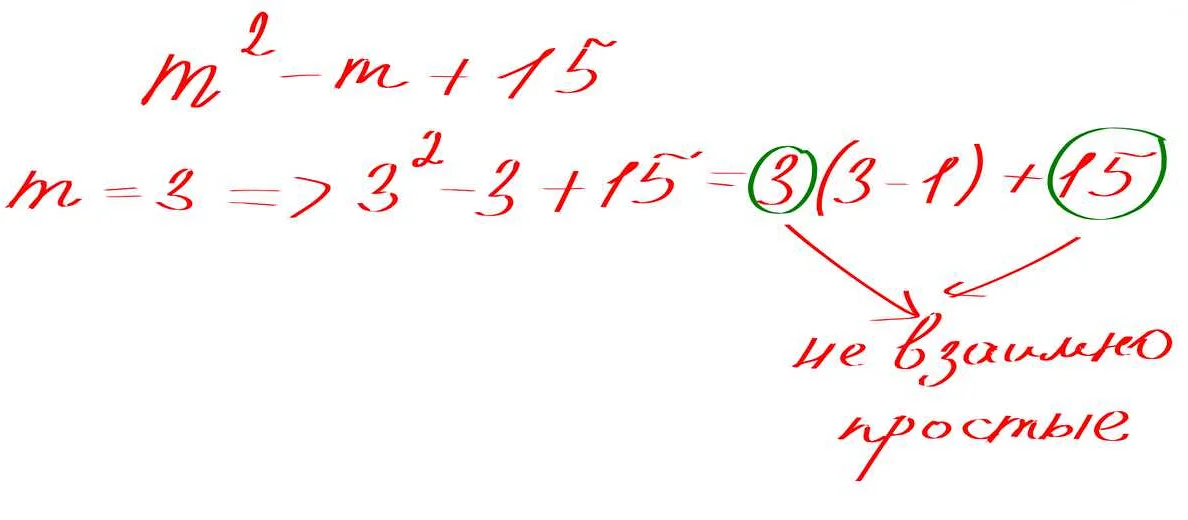




Очень интересная статья! Я всегда задумывалась о том, что такое счастливое число в математике. Оказывается, это число, которое при разбиении его на две равные части и сложении этих частей даёт в результате одно и то же число. Например, число 7 является счастливым, потому что 7 = 3 + 4. А число 19 не является счастливым, потому что 19 ≠ 9 + 10. Счастливые числа имеют свои удивительные свойства. Например, существуют бесконечные последовательности счастливых чисел. Мне нравится идея, что математика может быть связана с понятием счастья. Может быть, если мы найдём своё счастливое число, то станем немного счастливее? Ведь математика – это не просто скучные формулы, а настоящее искусство, которое может привнести радость и в нашу жизнь. Спасибо за интересную статью, я теперь знаю, что такое счастливое число!