Что такое сектор в математике
Содержимое
- 1 Что такое сектор в математике
Сектор в математике — это часть круга, ограниченная двумя радиусами и дугой. Узнайте, как вычислять площадь и длину дуги сектора, а также как использовать секторы в геометрии и тригонометрии.
В математике термин «сектор» имеет несколько значений, но общая идея остается неизменной — это часть круга, ограниченная двумя радиусами и дугой между ними. Секторы широко используются в геометрии, графике и других областях, где требуется работа с круговыми формами и углами.
В геометрии сектор может быть определен как фрагмент круга, который ограничен двумя радиусами и дугой между ними. Угол между радиусами, ограничивающими сектор, называется центральным углом. Длина дуги между радиусами также является важной характеристикой сектора.
Секторы могут быть различных типов в зависимости от их формы и размеров. Например, если центральный угол равен 90 градусам, сектор называется прямым. Если угол меньше 90 градусов, сектор называется острым, а если больше 90 градусов — тупым. Секторы могут быть использованы для вычисления площади части круга или для измерения времени в градусах на круговом графике.
Например, представьте себе пиццу, разделенную на несколько секторов. Каждый сектор представляет собой часть всей пиццы, и его размер определяется центральным углом. Если вы хотите узнать, сколько пиццы осталось, вы можете посчитать количество съеденных секторов и узнать их общую площадь.
Секторы также используются в графике для визуализации данных в виде круговых диаграмм. Каждый сектор на диаграмме представляет собой часть целого и может быть помечен процентом или числом, чтобы увидеть соотношение различных значений. Круговые диаграммы секторов широко используются в статистике, экономике, бизнесе и других областях, где важно визуализировать данные в простой и понятной форме.
Определение сектора в математике
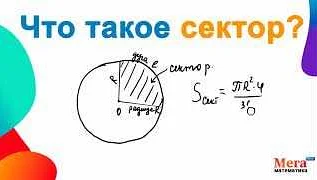
Для определения сектора необходимо знать его центр, радиус и меру угла дуги. Центр окружности является общим для всех радиусов и дуг, ограничивающих сектор. Радиус — это расстояние от центра окружности до любой точки на окружности. Мера угла дуги указывает, какую часть окружности занимает дуга, ограничивающая сектор.
Секторы могут быть различных размеров и форм. Например, сектор может занимать полную окружность, в этом случае его угол будет равен 360°. Сектор может быть также половиной окружности, третью, четвертью и т.д., в зависимости от меры угла дуги.
Секторы широко применяются в различных областях математики, физики и геометрии. Они позволяют анализировать и изучать различные свойства и взаимодействия фигур и объектов на плоскости.
Видео по теме:
Геометрическое представление сектора
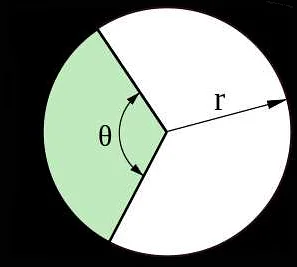
- Центр круга — точка, от которой проводятся радиусы
- Радиус — отрезок, соединяющий центр круга с точкой на окружности
- Дуга — часть окружности, которая соединяет две точки на окружности, ограниченные радиусами
Геометрическое представление сектора позволяет наглядно представить его форму и размеры. Оно может быть использовано для вычисления различных параметров сектора, таких как длина дуги, площадь сектора и центральный угол.
Например, представим сектор с радиусом 5 и центральным углом 60 градусов. Геометрическое представление этого сектора будет выглядеть как кусок окружности с радиусом 5 и углом в 60 градусов.
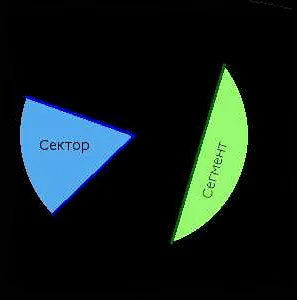
Различные типы секторов
В математике существуют различные типы секторов, которые могут быть определены в зависимости от их геометрических свойств:
1. Сектор полной окружности — это сектор, который занимает все пространство между двумя радиусами и дугой окружности. Угол этого сектора равен 360 градусам.
2. Сектор полукруга — это сектор, который занимает половину окружности. Угол этого сектора равен 180 градусам.
3. Сектор острого угла — это сектор, угол которого меньше 90 градусов. Этот сектор занимает менее половины окружности.
4. Сектор тупого угла — это сектор, угол которого больше 90 градусов, но меньше 180 градусов. Этот сектор занимает более половины окружности, но меньше ее полного объема.
5. Сектор правого угла — это сектор, угол которого равен 90 градусам. Этот сектор занимает половину окружности.
Таким образом, секторы могут иметь различные геометрические свойства в зависимости от их углового размера.
Формула для вычисления площади сектора
ОбозначениеОписание
| A | Площадь сектора |
| r | Радиус круга |
| θ | Центральный угол (в радианах) |
Формула для вычисления площади сектора:
A = (π * r^2 * θ) / 2
Где π (пи) – математическая константа, приближенное значение которой равно 3.14159.
Пример:
Пусть у нас есть круг с радиусом r = 5 см и центральным углом θ = 60°. Чтобы найти площадь сектора, мы можем использовать формулу:
A = (π * 5^2 * 60°) / 360° = (3.14159 * 25 * 60) / 360 ≈ 13.09 см²
Таким образом, площадь сектора равна примерно 13.09 квадратных сантиметров.
Примеры использования секторов в реальной жизни
Секторы находят свое применение в различных областях реальной жизни. Ниже представлены несколько примеров использования секторов:
- В географии: секторы используются для измерения углов и определения направлений на карте или компасе. Например, сектор может быть использован для указания направления на север, юг, восток или запад.
- В архитектуре: секторы используются для планирования и размещения элементов зданий. Например, сектор может определить расположение окна или двери относительно других элементов здания.
- В финансовой сфере: секторы могут использоваться для анализа рынков и разделения активов по различным секторам экономики. Например, финансовый аналитик может разделить акции компаний по секторам, таким как технологии, здравоохранение или энергетика.
- В спорте: секторы используются для отображения различных зон или секторов на спортивных аренах. Например, на футбольном стадионе секторы могут быть использованы для размещения болельщиков или для определения расположения игрового поля.
- В медицине: секторы могут использоваться для измерения углов и определения областей внутри организма. Например, сектор может быть использован для определения размеров опухоли или для планирования хирургического вмешательства.
Это всего лишь несколько примеров использования секторов в реальной жизни. Секторы широко применяются в различных областях, где требуется измерение углов и определение областей. Изучение и понимание секторов в математике может быть полезным для решения задач во многих практических ситуациях.
Сектор в тригонометрии

Угловой сектор определяется длиной дуги окружности и радиусом. Длина дуги вычисляется по формуле:
L = r * θ,
где L — длина дуги, r — радиус окружности, θ — угол в радианах.
Площадь сектора вычисляется по формуле:
S = (1/2) * r^2 * θ,
где S — площадь сектора.
Сектор в тригонометрии используется для вычисления значений тригонометрических функций (синуса, косинуса, тангенса и др.) в заданных углах.
Например, если нам дан сектор с углом 60 градусов и радиусом 5, мы можем вычислить длину дуги окружности и площадь сектора с помощью соответствующих формул.
Интересные факты о секторах
- Площадь сектора можно вычислить по формуле S = (πr^2 * α) / 360, где r — радиус круга, α — центральный угол сектора.
- Частный случай сектора — полный круг с центральным углом 360°. Его площадь равна площади всего круга.
- Секторы могут быть использованы для вычисления вероятностей. Например, вероятность выпадения определенного числа на игральной кости можно выразить как отношение площади сектора, соответствующего этому числу, к площади всего круга.
- Секторы используются в навигации, особенно в аэронавтике. Например, радиолокационные системы используют сектора для определения направления и дальности объектов.
- Секторы также находят применение в статистике и экономике. Например, секторная модель может быть использована для анализа структуры рынка или распределения занятости по отраслям.
Эти факты демонстрируют разнообразие применений и важность секторов в различных областях науки и жизни.
Вопрос-ответ:
Что такое сектор в математике?
Сектор в математике — это часть круга, ограниченная двумя радиусами и дугой между ними.
Как определить площадь сектора?
Площадь сектора можно определить с помощью формулы: S = (α/360°) * π * r^2, где α — центральный угол сектора, r — радиус круга.
Как найти длину дуги сектора?
Длина дуги сектора вычисляется по формуле: L = (α/360°) * 2 * π * r, где α — центральный угол сектора, r — радиус круга.
Какие примеры секторов можно привести?
Примеры секторов могут быть разнообразными. Например, если взять сектор круга, в котором центральный угол составляет 90°, то это будет четверть круга. А если взять сектор с центральным углом 180°, то это будет половина круга.
Как использовать понятие сектора в практических задачах?
Понятие сектора широко применяется в различных областях, например, для вычисления площади поля, огорода или круглого стола. Также секторы используются при расчете времени в шкалах часов или для определения доли целого в процентах.



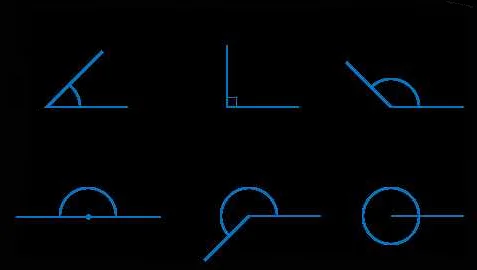
Очень интересная и познавательная статья! Я всегда был любителем математики, но не всегда понимал все тонкости и определения. Спасибо за то, что разъяснили, что такое сектор в математике. Теперь мне стало гораздо понятнее, что это такое и как его можно использовать. Примеры, которые вы привели, помогли мне лучше представить себе эту концепцию. Теперь я смогу применять ее в будущем и использовать в решении различных задач. Очень рад, что наткнулся на вашу статью, и очень рекомендую ее прочитать всем, кто интересуется математикой и хочет расширить свои знания.
Спасибо за интересную и познавательную статью! Я всегда хотела разобраться в понятии «сектор» в математике. Теперь я понимаю, что сектор — это часть круга, ограниченная двумя радиусами и дугой между ними. Важно помнить, что сектор задается углом, который измеряется в радианах или градусах. Примеры, которые вы привели, помогли мне лучше осознать эту концепцию. Теперь я могу представить себе, как секторы используются в геометрии и статистике. Эта информация отлично дополнит мои знания и поможет применять математику в повседневной жизни. Спасибо за разъяснения!