Что такое развернутый угол в математике 6
Содержимое
- 1 Что такое развернутый угол в математике 6
- 1.1 Развернутый угол: общее понятие и определение
- 1.2 Как определить развернутый угол: основные признаки и свойства
- 1.3 Развернутый угол: углы поворота и их величина
- 1.4 Простые примеры расчета развернутого угла
- 1.5 Сложные примеры расчета развернутого угла
- 1.6 Практическое применение развернутого угла в геометрии
- 1.7 Вопрос-ответ:
- 1.7.0.1 Что такое развернутый угол?
- 1.7.0.2 Каковы особенности развернутого угла?
- 1.7.0.3 Как можно представить развернутый угол геометрически?
- 1.7.0.4 Как можно вычислить меру развернутого угла?
- 1.7.0.5 Какие примеры можно привести для лучшего понимания развернутого угла?
- 1.7.0.6 Что такое развернутый угол в математике?
- 1.7.0.7 Как можно рассчитать развернутый угол?
- 1.8 Как использовать развернутый угол при решении математических задач
- 1.9 Видео по теме:
Развернутый угол в математике 6 — это угол, который открывает своими сторонами полную окружность. Ученикам 6 класса важно понимать и уметь измерять развернутый угол, так как это основа для изучения геометрии и решения различных задач. В данной статье вы найдете подробное объяснение понятия развернутого угла и примеры его использования в математических задачах.
Развернутый угол — это особая форма угла, который имеет степень 180. В математике 6-го класса развернутый угол рассматривается как одна из ключевых концепций геометрии.
Развернутый угол может представлять собой полный поворот или вращение вокруг точки. В геометрии, развернутый угол является важным элементом для изучения, поскольку он позволяет определить различные формы и свойства фигур.
Например, если мы возьмем круг и разделим его на две части, каждая из которых составляет 180 градусов, то получим два развернутых угла.
Для определения развернутого угла, необходимо знать его степень. Полный поворот составляет 360 градусов, поэтому развернутый угол будет составлять половину от этой величины. Таким образом, развернутый угол всегда равен 180 градусам.
Развернутые углы встречаются в различных областях математики и физики. Они используются для измерения поворотов, а также для решения задач, связанных с геометрией и тригонометрией. Понимание и умение работать с развернутыми углами является важным навыком для успеха в этих областях науки.
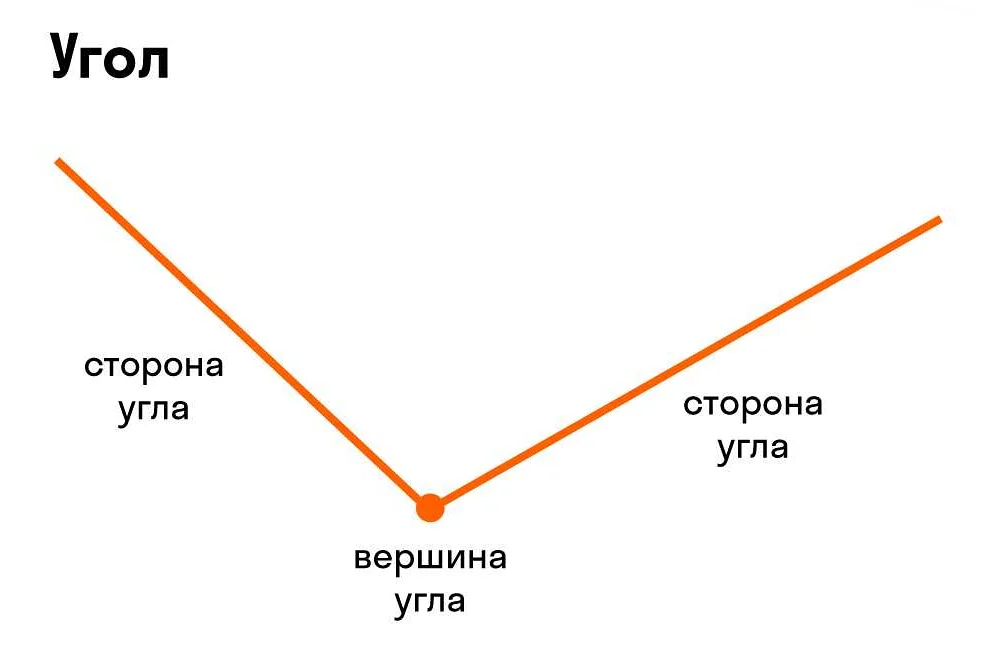
Развернутый угол: общее понятие и определение
Угол является развернутым, когда его конечные стороны лежат на одной прямой и образуют полный оборот вокруг вершины. Это значит, что начальная и конечная точки угла совпадают.
Развернутый угол может быть измерен как в градусах, так и в радианах. В градусах, развернутый угол равен 360°, а в радианах — 2π.
Развернутый угол широко используется в геометрии, физике, инженерии и других науках для измерения поворота, оборотов и циклических процессов.
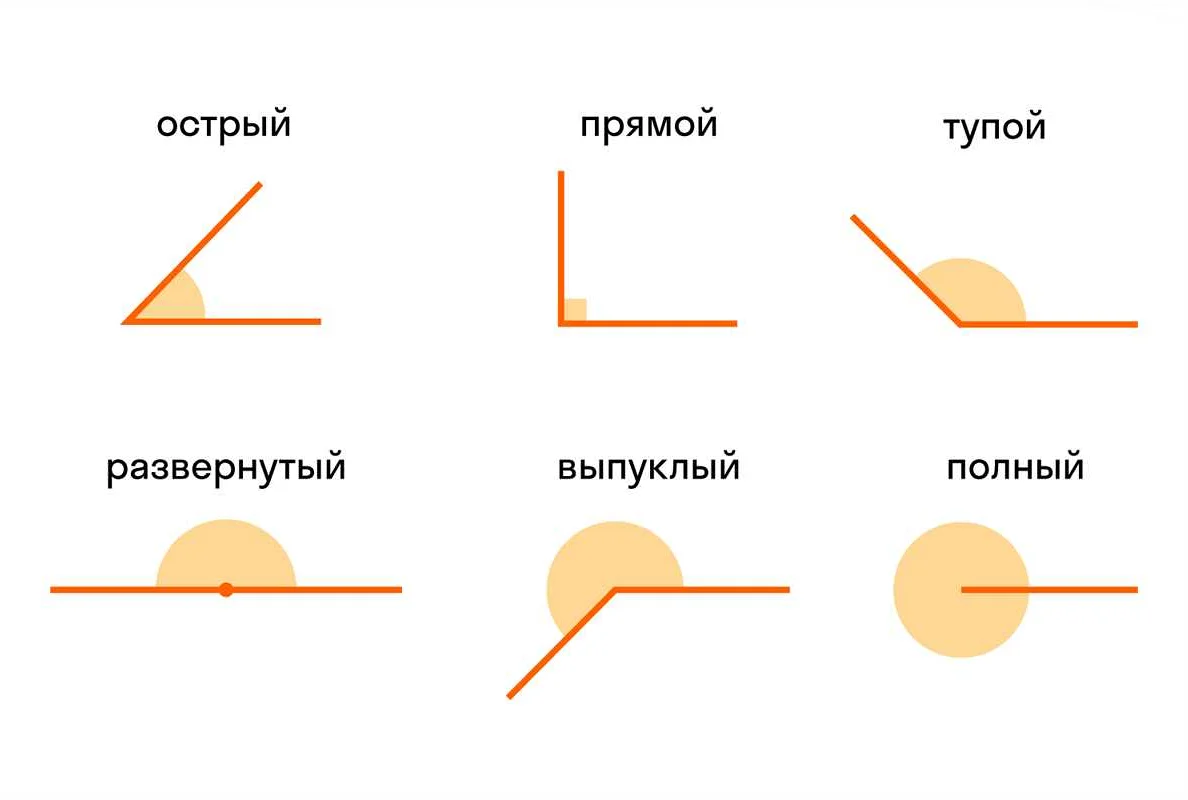
Как определить развернутый угол: основные признаки и свойства
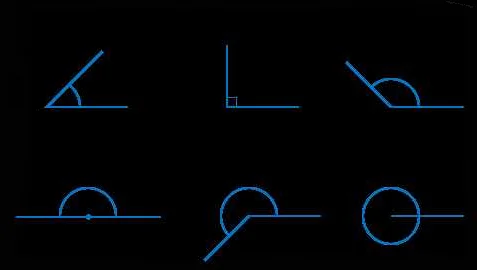
Основные признаки развернутого угла:
| 1. | Величина развернутого угла всегда равна 180 градусам или π радианам. |
| 2. | Угол может быть измерен с помощью градусной меры или радианной меры. |
| 3. | Развернутый угол можно представить как сумму двух прямых углов, каждый из которых равен 90 градусам или π/2 радианам. |
| 4. | Развернутый угол является самым большим углом, который может быть образован на плоскости. |
Свойства развернутого угла:
| 1. | Развернутый угол обладает свойством перестановки, то есть его можно поворачивать вокруг точки и он останется без изменений. |
| 2. | Сумма двух развернутых углов равна 360 градусам или 2π радианам, что соответствует полному обороту. |
| 3. | Развернутый угол обладает свойством равенства: если два угла имеют одинаковую величину, то они являются развернутыми углами. |
Развернутый угол: углы поворота и их величина

Углы поворота могут быть как положительными, так и отрицательными. Положительный поворот осуществляется по часовой стрелке, а отрицательный — против часовой стрелки.
Величина развернутого угла может быть выражена в градусах, радианах или оборотах. Чтобы перевести угол из градусов в радианы, нужно умножить его на π/180. Например, развернутый угол в 180 градусов будет равен π радианам.
Когда мы говорим о развернутом угле, обычно мы имеем в виду полный оборот. Но в математике также существуют углы поворота, которые меньше полного оборота. Например, половина оборота — 180 градусов или π радианов. Такие углы также являются развернутыми, но имеют меньшую величину.
Развернутый угол имеет важное значение в геометрии и физике. Он используется для описания поворотов объектов, например, в трехмерной графике или робототехнике. Также он применяется в тригонометрии для вычисления тригонометрических функций, таких как синус и косинус.
Простые примеры расчета развернутого угла
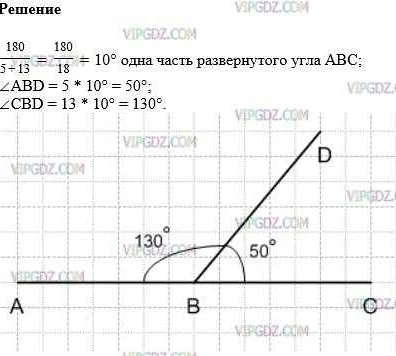
Рассмотрим простые примеры расчета развернутого угла:
Пример 1:
У нас есть полуокружность с радиусом 6 сантиметров. Найдем развернутый угол.
Решение:
Длина полуокружности равна π * (2 * радиус) = π * (2 * 6) = 12π см.
Для нахождения развернутого угла, мы делим длину полуокружности на радиус:
Развернутый угол = Длина полуокружности / Радиус = 12π / 6 = 2π радиан = 360 градусов.
Пример 2:
У нас есть треугольник с двумя сторонами длиной 3 см и 5 см, и углом между ними 90 градусов. Найдем развернутый угол.
Решение:
Сумма углов треугольника равна 180 градусов. Так как у нас есть прямой угол (90 градусов), то у нас остается только 180 — 90 = 90 градусов, которые нужно дополнить до развернутого угла.
Развернутый угол = 90 градусов + 90 градусов = 180 градусов.
Пример 3:
У нас есть окружность с диаметром 10 см. Найдем развернутый угол.
Решение:
Радиус окружности равен половине диаметра, то есть 10 / 2 = 5 см.
Длина окружности равна π * (2 * радиус) = π * (2 * 5) = 10π см.
Для нахождения развернутого угла, мы делим длину окружности на радиус:
Развернутый угол = Длина окружности / Радиус = 10π / 5 = 2π радиан = 360 градусов.
Это были простые примеры расчета развернутого угла. В реальных задачах развернутый угол может быть использован для решения различных геометрических и математических задач.
Сложные примеры расчета развернутого угла
Для более сложных примеров расчета развернутого угла нам понадобятся знания о формуле дуги и центральном угле.
Формула дуги гласит, что длина дуги окружности равна произведению меры центрального угла и радиуса окружности. То есть, если у нас есть окружность с радиусом 5 см и центральным углом в 60 градусов, то длина дуги будет равна 60 градусов * 5 см = 300 см.
Теперь рассмотрим более сложный пример. Предположим, у нас есть окружность с радиусом 4 см и центральным углом в 120 градусов. Мы хотим найти длину дуги этой окружности.
Для начала, воспользуемся формулой дуги: длина дуги = мера центрального угла * радиус. В нашем случае, длина дуги = 120 градусов * 4 см = 480 см.
Таким образом, длина дуги этой окружности составляет 480 см.
Используя эти примеры, мы можем рассчитать развернутый угол для различных окружностей с разными центральными углами и радиусами. Это позволяет нам лучше понимать, как изменение меры центрального угла и радиуса влияет на длину дуги.
Практическое применение развернутого угла в геометрии
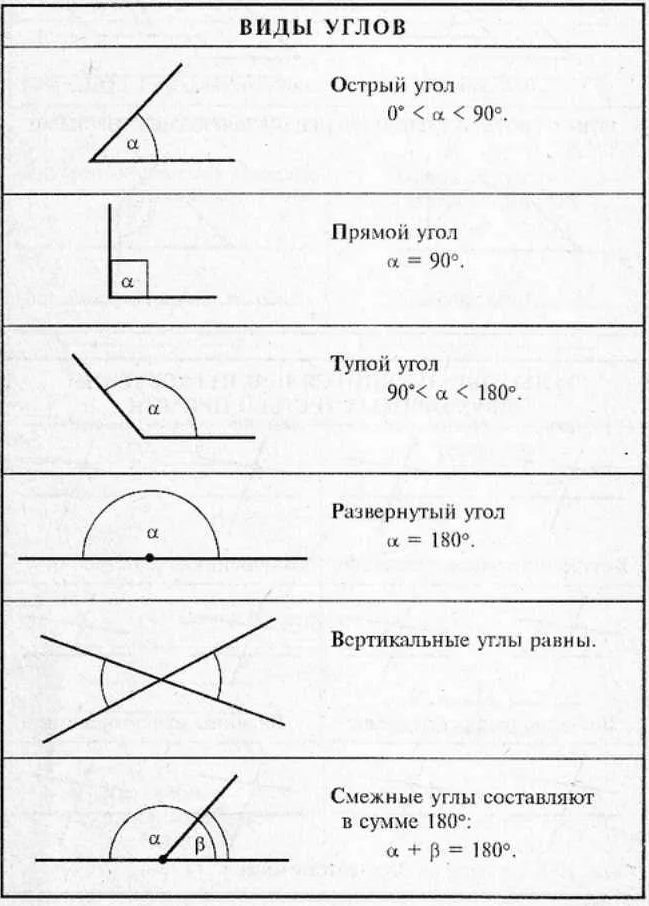
Развернутый угол имеет широкое практическое применение в геометрии. Он используется для измерения градусной меры поворота вокруг точки. Развернутый угол также помогает определить полный оборот или окружность.
Одним из практических применений развернутого угла является определение угла между двумя линиями или плоскостями. Например, при изучении треугольников или многоугольников, развернутый угол помогает определить, являются ли они острыми, прямыми или тупыми.
Развернутый угол также используется при измерении вращательных движений в механике. Например, при анализе вращения колеса автомобиля или вентилятора, развернутый угол помогает определить, насколько объект повернулся относительно начального положения.
Кроме того, развернутый угол находит применение в навигации и геодезии. При определении направлений на карте или при изучении глобуса, развернутый угол помогает ориентироваться в пространстве и определить путь между двумя точками.
В заключение, развернутый угол является важным инструментом в геометрии и имеет широкое практическое применение. Он помогает измерять и описывать углы, повороты и направления в различных областях науки и техники.
Вопрос-ответ:
Что такое развернутый угол?
Развернутый угол — это угол, который поворачивается на 360 градусов, полностью образуя круг.
Каковы особенности развернутого угла?
Развернутый угол не имеет конкретной величины, так как он поворачивается на 360 градусов и образует полный круг.
Как можно представить развернутый угол геометрически?
Развернутый угол можно представить геометрически в виде полного круга или окружности, так как он поворачивается на 360 градусов.
Как можно вычислить меру развернутого угла?
Мера развернутого угла всегда равна 360 градусов.
Какие примеры можно привести для лучшего понимания развернутого угла?
Примерами развернутых углов могут быть: полный оборот стрелки часов, поворот колеса автомобиля на 360 градусов и т.д.
Что такое развернутый угол в математике?
Развернутый угол в математике — это угол, который имеет меру 360 градусов. Такой угол полностью охватывает всю окружность и является наибольшим из всех углов.
Как можно рассчитать развернутый угол?
Развернутый угол всегда равен 360 градусам. Это базовое свойство развернутого угла, которое можно использовать для простого расчета его меры.
Как использовать развернутый угол при решении математических задач
Развернутый угол имеет важное значение при решении различных математических задач. Он позволяет нам лучше понять геометрические отношения и использовать их для нахождения нужных величин.
Один из основных способов использования развернутого угла состоит в его разделении на равные части. Для этого мы можем использовать доли развернутого угла, такие как трети, половины или четверти. Зная, сколько частей составляет развернутый угол, мы можем определить, сколько градусов составляет каждая часть.
Развернутый угол также может быть использован для нахождения неизвестных углов. Например, если мы знаем, что сумма двух углов равна развернутому углу, а один из углов известен, мы можем найти второй угол, вычитая из развернутого угла известный угол.
Кроме того, развернутый угол может помочь нам находить отношения между углами в треугольниках. Например, если мы знаем, что два угла треугольника составляют развернутый угол, мы можем найти третий угол, вычитая из развернутого угла сумму двух известных углов.
Также развернутый угол может быть использован для решения задач на нахождение длины дуги окружности. Зная, что развернутый угол составляет определенную долю от развернутого угла окружности (например, треть или половину), мы можем найти длину дуги, используя формулу для длины дуги окружности.
В заключение, развернутый угол является полезным инструментом при решении различных математических задач. Он позволяет нам использовать геометрические отношения и находить нужные величины, разделять угол на равные части, находить неизвестные углы и решать задачи на нахождение длины дуги окружности. Понимание и использование развернутого угла поможет вам решать задачи более эффективно и точно.
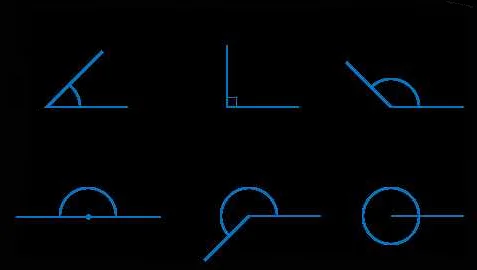


Статья очень понятно объясняет, что такое развернутый угол в математике. Я всегда думала, что углы бывают только прямые, острые или тупые, но оказывается, развернутый угол — это угол, который больше прямого угла, но меньше полного. Теперь я знаю, что он равен 180 градусам. Мне понравился пример с расчетом развернутого угла. Автор подробно объяснил, как найти развернутый угол по известной величине другого угла. Я уже пробовала посчитать несколько примеров сама и у меня получается! Теперь я чувствую себя немного математиком. Спасибо, статья помогла мне разобраться с этим понятием. Жду новых материалов на эту тему!