Что такое sgn в математике

Sgn (знак) является математической функцией, которая определяет положительность или отрицательность числа. Узнайте, как использовать функцию sgn и как она может помочь в анализе математических выражений.

sgn — это сокращение от латинского термина signum, что в переводе означает «знак». В математике sgn — это функция, которая позволяет определить знак числа. Она возвращает одно из трех значений: 1, если число положительное; -1, если число отрицательное; и 0, если число равно нулю.

Функция sgn широко применяется в различных областях математики. Например, она используется при решении уравнений и неравенств, а также при анализе и определении поведения функций. Благодаря sgn можно определить, куда будет двигаться график функции при приближении к нулю, и какие значения функция принимает в разных интервалах.

Например, функция f(x) = x / |x| не является определена при x = 0, но можно определить ее значение при приближении к нулю. В этом случае, используя функцию sgn, можно записать f(x) = sgn(x), которая принимает значения 1 и -1 в зависимости от знака x.

Таким образом, понимание и использование функции sgn позволяет упростить и улучшить анализ и решение математических задач, связанных с определением знака числа и анализом функций.

Основные понятия sgn в математике

Функция sgn (signum) представляет собой математическую функцию, которая возвращает знак числа. Знак числа может быть положительным, отрицательным или нулевым. Функция sgn присваивает следующие значения:

• sgn(x) = 1, если x > 0;
• sgn(x) = -1, если x < 0;
• sgn(x) = 0, если x = 0.

Эта функция широко используется в математике и физике для решения различных задач. Например, она может быть использована для определения направления движения объекта, определения знака выражения или определения типа корней в уравнении.

Функция sgn может быть также использована для определения асимптотического поведения функции. Например, если предел функции при x, стремящемся к бесконечности, равен 1, то функция асимптотически приближается к y = 1, и sgn(x) = 1.

Принципы работы sgn в математике

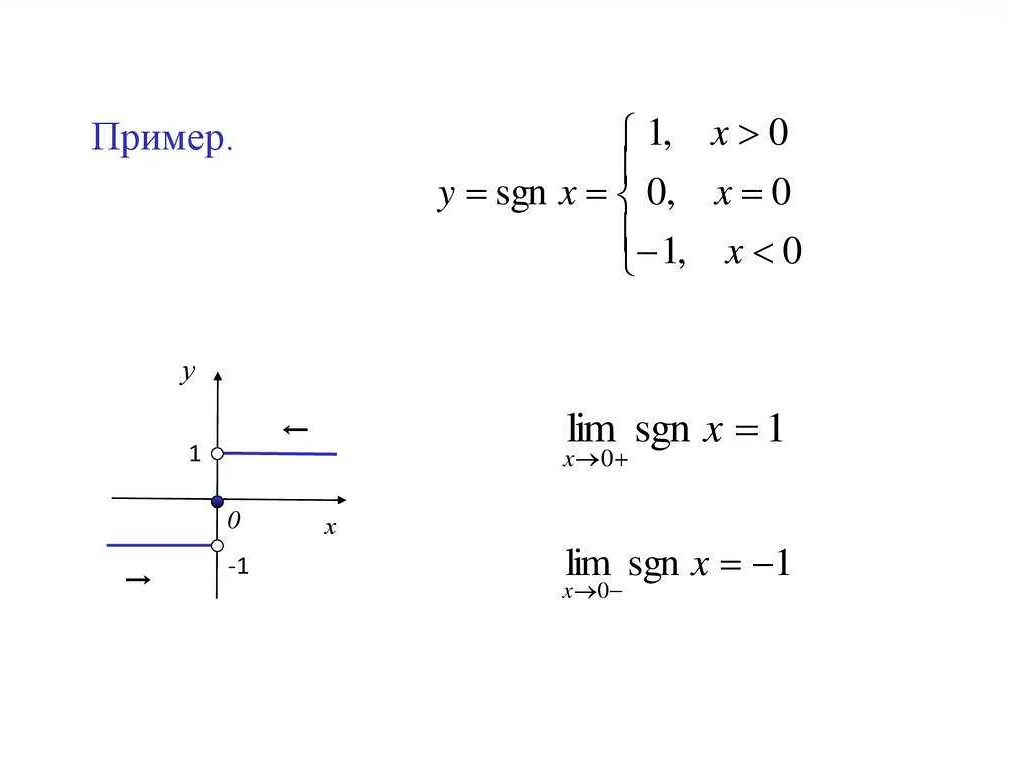
Принцип работы функции sgn очень прост: она принимает число в качестве аргумента и возвращает число, которое указывает на его знак. Если число положительное, функция возвращает 1. Если число отрицательное, функция возвращает -1. Если число равно нулю, функция возвращает 0.

Применение функции sgn в математике очень широко. Она может быть использована для решения различных задач, таких как определение наибольшего и наименьшего значения из нескольких чисел, построение графиков функций, анализ изменения знака функции и многое другое.

Также функция sgn может быть использована для решения практических задач. Например, она может быть полезна при решении физических задач, связанных с определением направления движения тела или определением значений функций, зависящих от знака чисел.

В заключение, функция sgn — это мощный инструмент математики, который позволяет упростить решение различных задач и анализировать различные процессы, связанные с знаками чисел.

Математические операции с использованием sgn

xsgn(x)

x > 0	1
x = 0	0
x < 0	-1

Функция sgn часто используется для определения направления или ориентации векторов, для проверки на знак числа или в вычислениях с комплексными числами.

Применение функции sgn в математических операциях позволяет упростить выражения и облегчить их анализ. Например, при расчете модуля разности двух чисел можно использовать следующую формулу:

|a — b| = sgn(a — b) * (a — b)

Использование функции sgn позволяет избавиться от модуля и упростить выражение. Если разность a — b положительна, то sgn(a — b) будет равно 1, и выражение примет вид:

|a — b| = (a — b)

Если разность a — b отрицательна, то sgn(a — b) будет равно -1, и выражение примет вид:

|a — b| = -(a — b)

Таким образом, функция sgn позволяет представить выражения более компактно и удобно для анализа.

Примеры использования sgn в математике

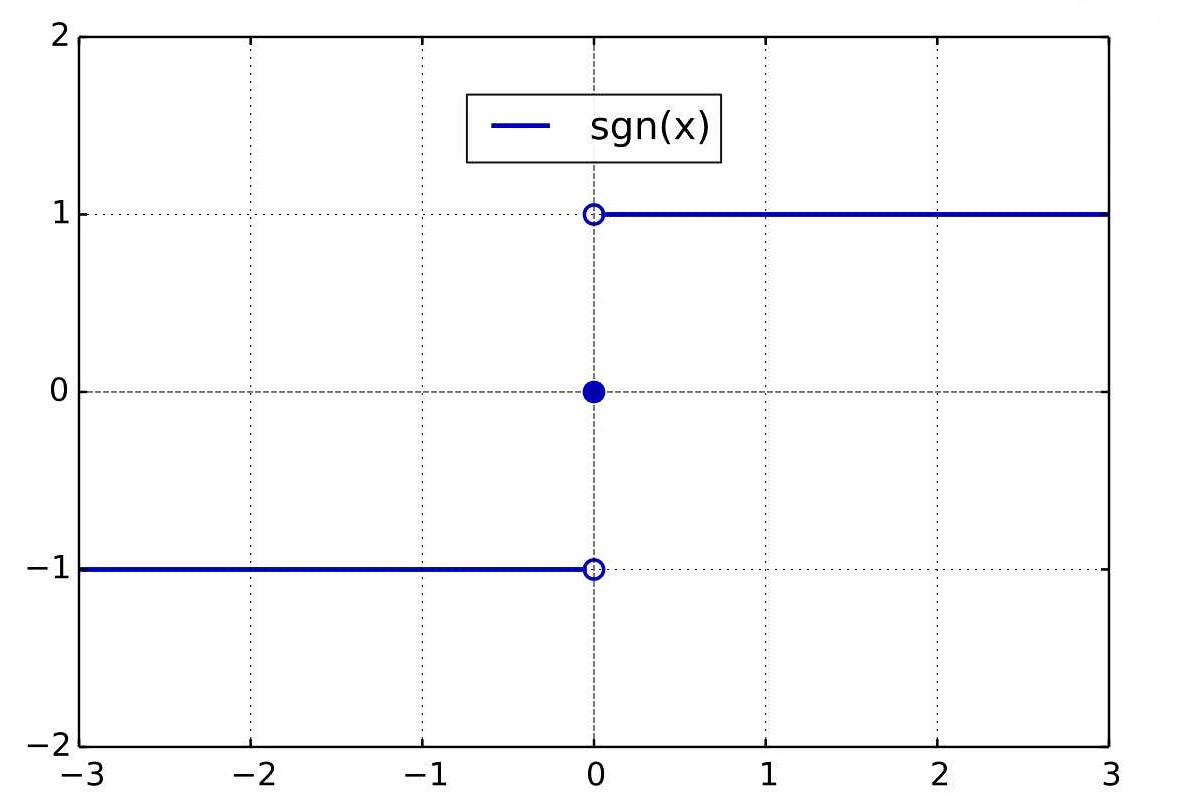
Функция sgn(x) в математике используется для определения знака числа x. Она возвращает -1, если число отрицательное, 0, если число равно нулю, и 1, если число положительное.

Ниже приведены примеры использования функции sgn:

Числоsgn

5	1
-3	-1
0	0
2.5	1
-7.8	-1

Таким образом, функция sgn позволяет быстро определить знак числа и использовать эту информацию в дальнейших математических вычислениях.

Значение sgn в тригонометрии

Функция sgn (сигнум) в тригонометрии используется для определения знака значения тригонометрических функций.

В тригонометрии сигнум задается следующим образом:

• sgn(x) = -1, если x < 0;
• sgn(x) = 0, если x = 0;
• sgn(x) = 1, если x > 0.

Данное определение позволяет определить знак синуса, косинуса и тангенса угла в тригонометрических функциях.

Например, если значение синуса угла равно 0, то sgn(sin(x)) = 0. Если значение синуса положительно, то sgn(sin(x)) = 1, а если отрицательно, то sgn(sin(x)) = -1.

Аналогично, можно определить знак косинуса и тангенса угла в тригонометрических функциях.

Использование функции sgn в тригонометрии позволяет упростить и анализировать значения тригонометрических функций в различных задачах.

sgn в линейной алгебре

Функция sgn возвращает:

• 1, если число положительное;
• 0, если число равно нулю;
• -1, если число отрицательное.

В линейной алгебре функция sgn часто используется для решения задач, связанных с определением направления векторов или определителей матриц.

Например, при вычислении определителя квадратной матрицы, знак определителя можно определить с помощью функции sgn. Если определитель равен нулю, то матрица вырожденная и необратима, иначе она невырожденная и имеет обратную матрицу.

Также функция sgn может использоваться при нахождении собственных значений и собственных векторов матрицы.

Вопрос-ответ:

Что такое sgn в математике?

В математике sgn (сигнум) — это функция, которая возвращает знак числа. Если число положительное, то sgn вернет 1, если число отрицательное -1, а если число равно нулю, то sgn вернет 0.

Как определить значение sgn для числа?

Для определения значения sgn для числа нужно проверить его знак. Если число положительное, то значение sgn будет равно 1. Если число отрицательное, значение sgn будет равно -1. Если число равно нулю, то значение sgn будет равно 0.

Какую роль играет функция sgn в математике?

Функция sgn в математике играет роль определения знака числа. Она помогает определить, является ли число положительным, отрицательным или нулем. Также функция sgn может использоваться для решения некоторых математических задач и уравнений.

Как применяется функция sgn в математике?

Функция sgn может применяться в математике для решения некоторых задач, связанных с определением знака числа. Например, она может использоваться, чтобы найти значения выражений с абсолютными значениями, определить, является ли число положительным или отрицательным, а также для решения некоторых уравнений.

Можно ли использовать функцию sgn в программировании?

Да, функция sgn может использоваться в программировании для определения знака числа. В разных языках программирования она может иметь различные названия и синтаксис, но обычно выполняет ту же функцию — возвращает знак числа. Это может быть полезно, например, при написании условий и циклов, когда нужно проверить знак числа или выполнить какое-то действие в зависимости от его знака.

Что такое sgn в математике?

sgn в математике — это функция, которая возвращает знак числа. Она принимает в качестве аргумента число и возвращает -1, 0 или 1 в зависимости от знака числа: отрицательное число -1, ноль 0 и положительное число 1.

Какие применения у функции sgn?

Функция sgn в математике широко используется в различных областях. Например, она может быть полезной при решении задач, связанных с определением симметрии графиков функций. Также функция sgn может использоваться в анализе изменения производной функции в разных точках и определении экстремумов.

Функциональные свойства sgn

Функция sgn(x) определена для всех действительных чисел x, кроме нуля. Ее значения могут быть только -1, 0 или 1, в зависимости от знака аргумента x.

1. Свойство знаков

Если x > 0, то sgn(x) = 1.

Если x < 0, то sgn(x) = -1.

Если x = 0, то sgn(x) = 0.

2. Свойство неотрицательности

Для любого x ≥ 0, sgn(x) ≥ 0.

3. Обратные знаки

sgn(x) = -sgn(-x) для любого x ≠ 0.

Эти свойства sgn являются основополагающими и используются при решении различных математических задач. Они позволяют определить знаки чисел и сравнивать их между собой. Например, с помощью функции sgn можно определить, какой из двух чисел больше или меньше другого, или решить уравнение с модулем.

Видео по теме: