Что такое функция в математике кратко

Функция в математике — это отношение между входными и выходными значениями. Она определяет, как одни значения зависят от других и может быть представлена графически, аналитически или в виде таблицы. Функции играют ключевую роль в решении математических задач и моделировании реальных процессов.

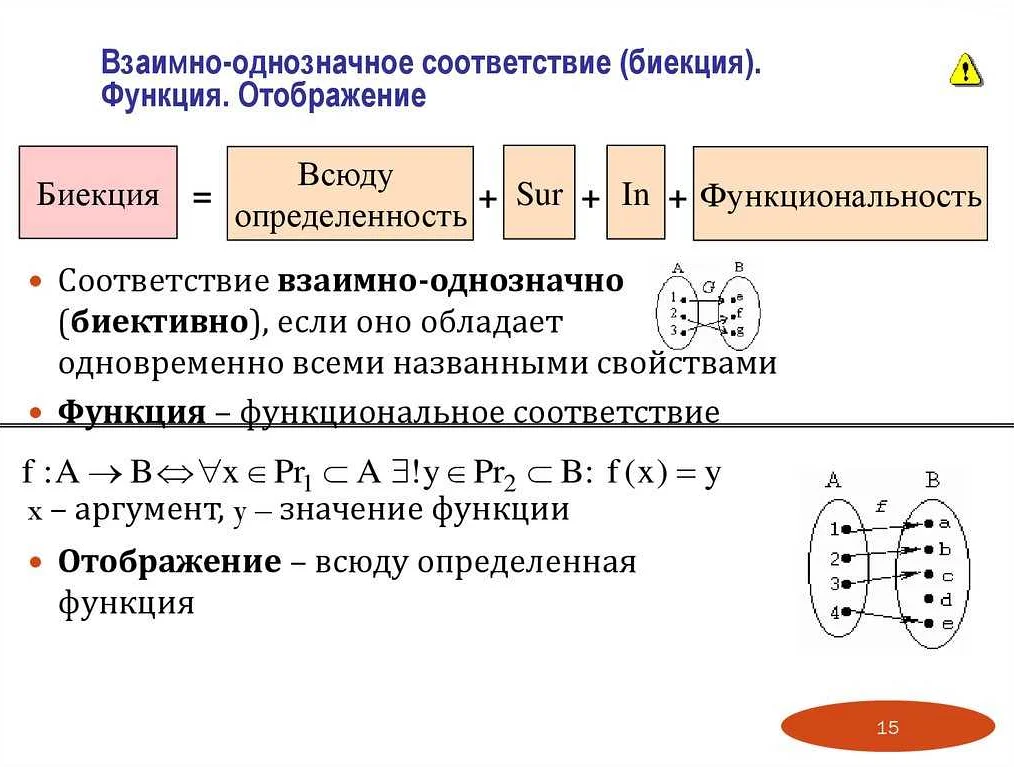
Функция — одно из важнейших понятий в математике, которое позволяет описывать зависимость одних величин от других. Она представляет собой особый вид соответствия между двумя множествами, где каждому элементу из одного множества сопоставляется ровно один элемент из другого множества.

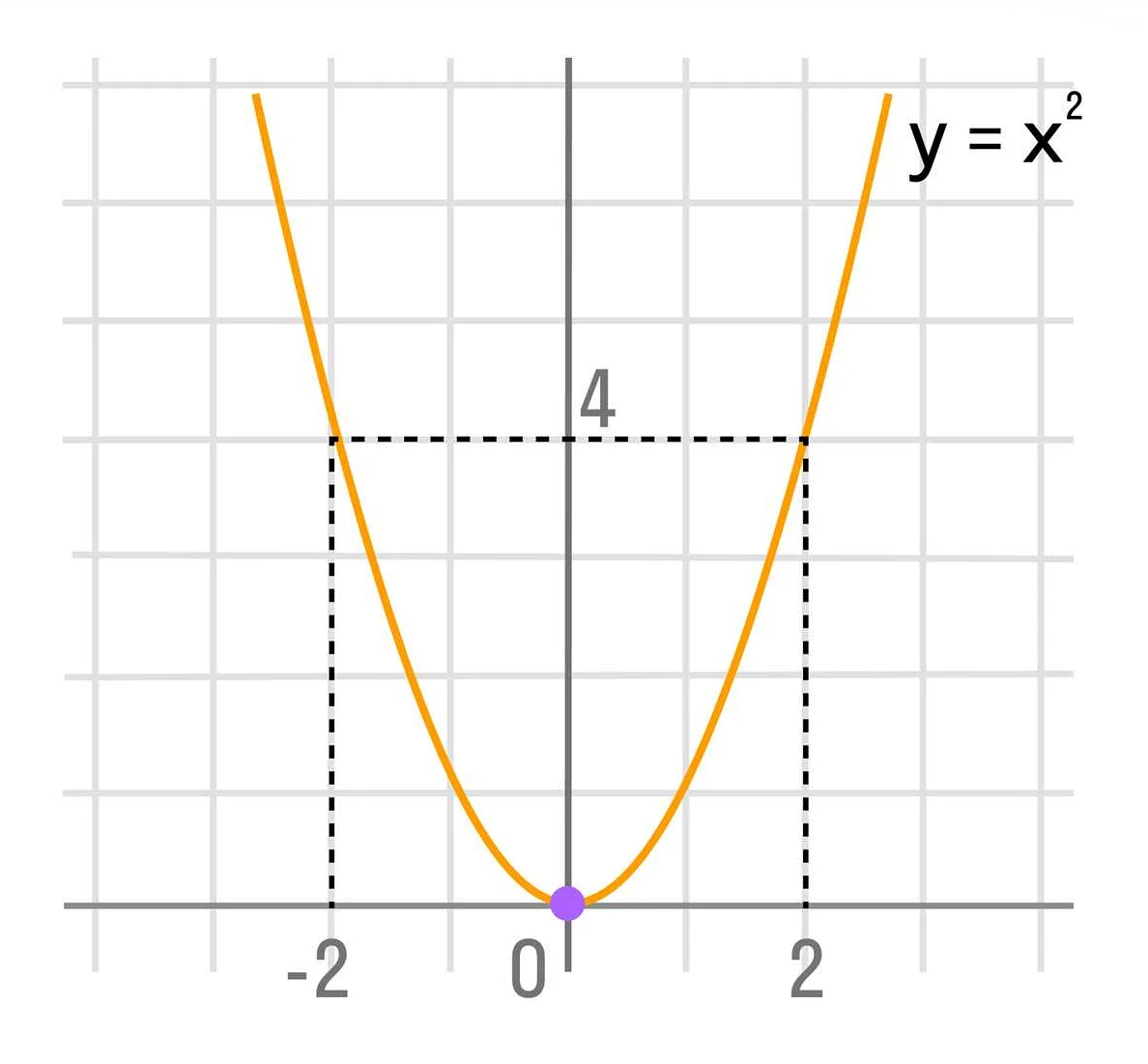
Определение функции включает в себя область определения и правило соответствия. Область определения — это множество значений, для которых функция определена. Правило соответствия задает способ получения значения функции по заданному аргументу. Например, функция f(x) = x^2 имеет область определения всех действительных чисел, а правило соответствия гласит, что значение функции равно квадрату аргумента.

Пример: пусть имеется функция f(x) = 2x + 1. Если подставить в нее значение x = 3, то получим f(3) = 2 * 3 + 1 = 7. Таким образом, значение функции при аргументе 3 будет равно 7.

Функции могут быть представлены различными способами, например, аналитически, графически или в виде таблицы значений. График функции — это графическое представление зависимости значений функции от аргументов. Он позволяет визуально исследовать основные свойства функции, такие как периодичность, монотонность, экстремумы и прочее.

Определение функции в математике

Область определения функции — это множество всех значений, для которых функция определена. Область значений функции — это множество всех значений, которые функция может принимать.

Функция обозначается с использованием символа f, за которым следует входной параметр в круглых скобках. Например, f(x) — это функция, которая принимает значение x в качестве входного параметра.

Функция может быть представлена различными способами, такими как график, таблица значений или алгебраическое выражение. В математике функции широко используются для моделирования и анализа различных явлений и процессов.

Основные понятия, связанные с функцией в математике

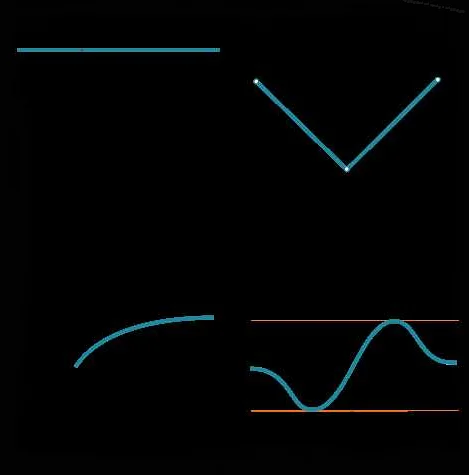
Основные элементы функции:

1. Область определения — множество всех возможных входных значений функции. Обозначается обычно как D или dom(f).

2. Область значений — множество всех возможных выходных значений функции. Обозначается обычно как R или range(f).

3. Значение функции — результат отображения входного значения на выходное значение. Обозначается как f(x), где x — входное значение.

4. График функции — множество всех точек (x, f(x)), где x принадлежит области определения функции.

Примерами функций могут служить:

— Функция f(x) = x^2, где x — любое вещественное число. Область определения — все вещественные числа, область значений — все неотрицательные вещественные числа.

— Функция g(x) = sin(x), где x — любое вещественное число. Область определения — все вещественные числа, область значений — все числа от -1 до 1.

Изучение функций в математике позволяет решать различные задачи, моделировать реальные процессы и анализировать их свойства.

Понятие области определения и области значений функции

Область определения функции — это множество значений, для которых функция определена. В других словах, это множество всех входных значений функции, которые приводят к определенному выходному значению. Область определения может быть ограничена или неограничена. Например, функция f(x) = 1 / x имеет область определения x ≠ 0, так как нельзя делить на ноль.

Область значений функции — это множество всех возможных значений, которые функция может принимать. В других словах, это множество всех выходных значений функции. Область значений может быть ограничена или неограничена. Например, функция f(x) = x^2 имеет область значений y ≥ 0, так как квадрат числа всегда положителен или равен нулю.

Знание области определения и области значений функции позволяет более точно определить характеристики функции, такие как монотонность, ограниченность, симметрию и т.д. Также, знание этих понятий помогает избегать ошибок при работе с функциями и решении математических задач.

Типы функций в математике: линейная, квадратичная и т.д.

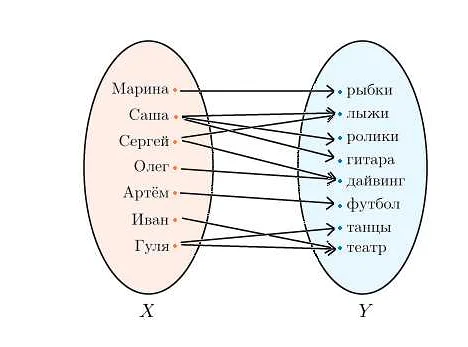
В математике существует множество типов функций, каждый из которых имеет свои особенности и свойства. Рассмотрим некоторые из наиболее распространенных типов функций:

Тип функцииОпределениеПример

Линейная функция	Функция, заданная уравнением вида y = kx + b, где k и b — константы.	y = 2x + 3
Квадратичная функция	Функция, заданная уравнением вида y = ax^2 + bx + c, где a, b и c — константы.	y = 3x^2 — 2x + 1
Показательная функция	Функция, заданная уравнением вида y = a^x, где a — положительное число, a ≠ 1.	y = 2^x
Логарифмическая функция	Функция, обратная к показательной функции и заданная уравнением вида y = loga(x), где a — положительное число, a ≠ 1.	y = log2(x)

Это лишь некоторые из множества типов функций, с которыми можно столкнуться в математике. Каждый тип функции имеет свои характеристики и применения в различных областях науки и техники.

Примеры функций в математике

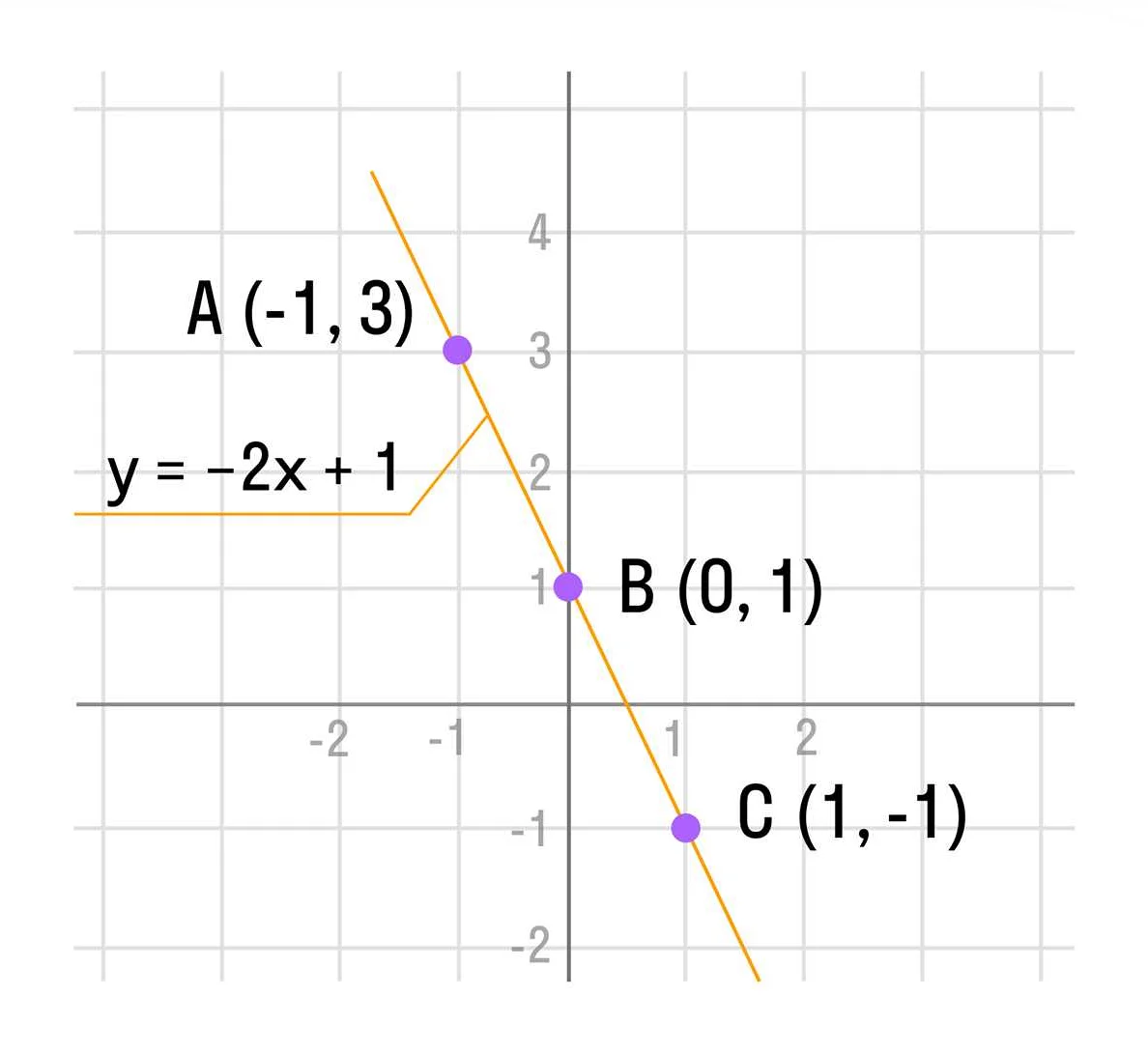
В математике существует множество различных примеров функций, которые помогают нам понять и изучить различные аспекты этого понятия. Рассмотрим несколько примеров функций:

• Линейная функция: одна из наиболее простых и широко используемых функций. Она задается уравнением вида y = ax + b, где a и b — константы, а x — переменная. График линейной функции представляет собой прямую линию.
• Квадратичная функция: функция, заданная уравнением вида y = ax^2 + bx + c. График квадратичной функции имеет форму параболы.
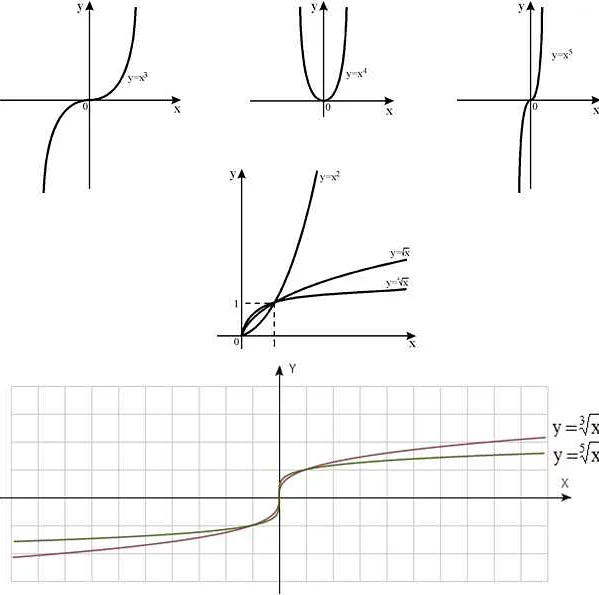
• Степенная функция: функция, заданная уравнением вида y = ax^n, где a и n — константы. График степенной функции зависит от значения показателя степени n.
• Тригонометрическая функция: функция, которая зависит от угла и отношения сторон в прямоугольном треугольнике. Примеры таких функций: синус, косинус, тангенс.
• Экспоненциальная функция: функция, заданная уравнением вида y = a^x, где a — константа. График экспоненциальной функции имеет вид параболы, которая растет или убывает в зависимости от значения a.
• Логарифмическая функция: обратная к экспоненциальной функции. Она задается уравнением вида y = log_a(x), где a — константа. График логарифмической функции представляет собой кривую линию.

Это лишь несколько примеров функций, которые используются в математике. Каждая из них имеет свои особенности и свой график, что позволяет изучать различные явления и закономерности в природе и обществе.

Значение функции в заданной точке

Рассмотрим пример функции f(x) = 2x + 3. Чтобы найти значение этой функции в заданной точке, например, в точке x = 5, необходимо подставить значение x = 5 вместо x в формулу функции:

Заданная точка (x)Функция (f(x) = 2x + 3)

5	2 * 5 + 3 = 10 + 3 = 13

Таким образом, значение функции f(x) = 2x + 3 в заданной точке x = 5 равно 13.

Значение функции в заданной точке может иметь как положительные, так и отрицательные значения, а также может быть равно нулю. В зависимости от формулы функции и значения аргумента, значение функции в заданной точке может меняться.

График функции и его основные характеристики

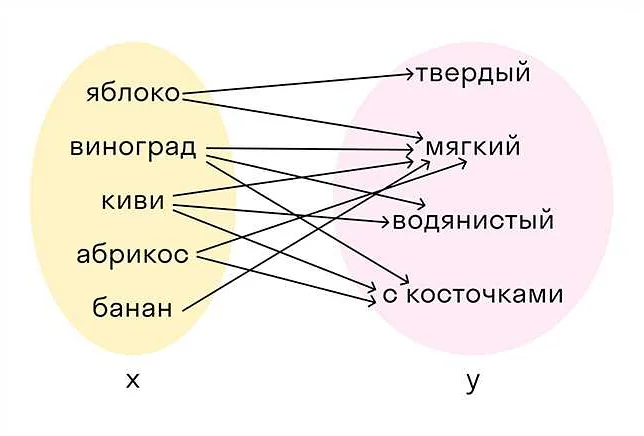
Основные характеристики графика функции включают:

• Область определения — это множество всех возможных входных значений функции. График функции присутствует только в пределах области определения.
• Область значений — это множество всех возможных выходных значений функции. График функции содержит только те точки, которые принадлежат области значений.
• Монотонность — это свойство функции, определяющее, как меняется ее значения при изменении входных значений. Функция может быть возрастающей (значения увеличиваются) или убывающей (значения уменьшаются).
• Экстремумы — это точки на графике функции, в которых она достигает максимального или минимального значения. Максимум — это точка, в которой функция имеет наибольшее значение, а минимум — наименьшее значение.
• Асимптоты — это прямые линии, которые график функции может приближаться, но никогда не пересекать. Асимптоты могут быть вертикальными (параллельны оси y) или горизонтальными (параллельны оси x).
• Точки перегиба — это точки на графике функции, в которых меняется выпуклость или вогнутость графика. В точке перегиба вторая производная функции равна нулю.

Изучение графика функции и его основных характеристик позволяет более глубоко понять поведение функции и использовать эту информацию в решении различных математических задач.

Применение функций в реальной жизни и науке

Применение функций в реальной жизни:

1. Функции используются в физике для описания движения тел, электрических и магнитных полей, распространения звука и света, а также других явлений природы.
2. В экономике функции помогают моделировать и анализировать процессы производства, спроса и предложения, инвестиций и экономического роста.
3. В медицине функции используются для моделирования физиологических процессов в организме, прогнозирования распространения болезней и оптимизации процессов лечения.
4. Функции находят применение в архитектуре и дизайне, помогая создавать оптимальные формы и конструкции.
5. В транспорте функции используются для оптимизации маршрутов, управления трафиком и моделирования движения транспортных средств.

Применение функций в науке:

1. Математические функции широко используются в физике, химии, биологии и других естественных науках для описания и анализа различных закономерностей и явлений.
2. Функции играют важную роль в компьютерных науках и информатике, где они используются для моделирования и оптимизации алгоритмов, анализа данных, искусственного интеллекта и других задач.
3. В экономической и социологической науке функции применяются для моделирования поведения рынков, прогнозирования трендов и анализа социальных процессов.
4. Функции также находят применение в статистике, где они используются для анализа данных, построения моделей и прогнозирования.
5. В инженерии функции применяются для проектирования и оптимизации систем, разработки новых технологий и улучшения существующих процессов.

Таким образом, функции играют важную роль в реальной жизни и науке, помогая анализировать данные, строить модели и принимать решения. Их применение охватывает широкий спектр областей и позволяет получать новые знания и достижения.

Вопрос-ответ:

Что такое функция в математике?

Функция в математике — это отображение между двумя множествами, где каждому элементу из одного множества ставится в соответствие элемент из другого множества. Она является основным понятием математического анализа и используется для описания зависимости между переменными.

Какие основные понятия связаны с функцией?

Основные понятия, связанные с функцией, — это область определения, область значений, график функции и обратная функция. Область определения — это множество значений переменной, для которых функция определена. Область значений — это множество значений, которые функция может принимать. График функции — это геометрическое представление зависимости между переменными. Обратная функция — это функция, обратная исходной функции.

Как можно задать функцию?

Функцию можно задать разными способами. Один из способов — это аналитический способ, когда функцию задают с помощью формулы или уравнения. Например, функцию y = 2x + 3 можно задать аналитически. Еще один способ — это графический способ, когда функцию задают с помощью графика. Например, функция y = x^2 + 1 можно задать графически.

Какие есть примеры функций в математике?

В математике есть множество примеров функций. Некоторые из них: линейная функция, квадратичная функция, показательная функция, логарифмическая функция, тригонометрическая функция. Например, функция y = 2x + 3 — это линейная функция, функция y = x^2 + 1 — это квадратичная функция, функция y = 2^x — это показательная функция, функция y = log(x) — это логарифмическая функция, функция y = sin(x) — это тригонометрическая функция.

Какие свойства имеет функция?

Функция имеет ряд свойств. Одно из основных свойств — это однозначность, то есть каждому элементу из области определения соответствует единственный элемент из области значений. Также функция может быть непрерывной или разрывной. Непрерывная функция — это функция, которая не имеет разрывов на своей области определения. Разрывная функция — это функция, которая имеет разрывы на своей области определения.

Что такое функция в математике?

Функция в математике — это математическое отображение, которое связывает каждый элемент одного множества, называемого областью определения, с единственным элементом другого множества, называемого областью значений. Функции широко используются в математике для описания зависимостей между величинами и решения различных задач.

Как определить функцию в математике?

Функция определяется двумя множествами — областью определения и областью значений. Область определения — это множество всех возможных входных значений, для которых функция определена. Область значений — это множество всех возможных выходных значений, которые функция может принимать. Каждому элементу из области определения функция ставит в соответствие ровно один элемент из области значений.

Видео по теме: