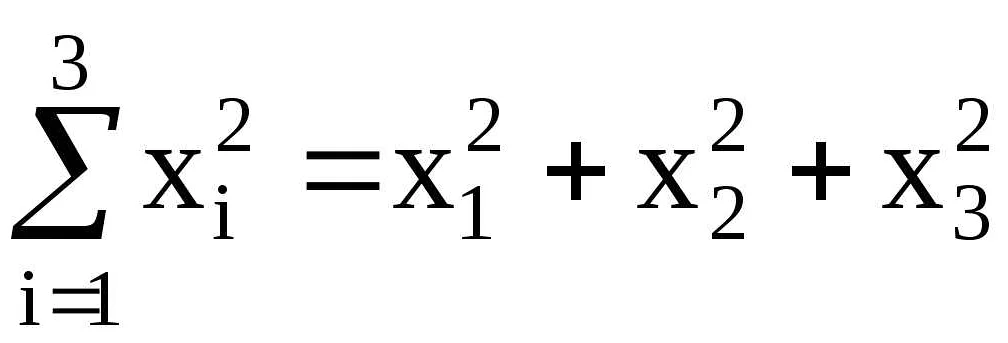Что в математике означает сигма

Сигма в математике означает сумму элементов последовательности или множества. Узнайте, как использовать символ сигма в вычислениях и формулах.

Сигма, обозначаемая символом Σ (с большой буквы) или σ (с маленькой буквы), является одним из основных математических символов, используемых в алгебре и анализе. Сигма представляет собой сумму всех элементов последовательности или функции, удовлетворяющих некоторому условию.

Символ сигмы обычно записывается над или под индексом и содержит выражение, определяющее переменную, начальное значение, конечное значение и саму функцию или последовательность. Например, выражение Σi=1∞(i2) обозначает сумму всех квадратов натуральных чисел, начиная с 1 и до бесконечности.

Пример: Σi=1n(i) = 1 + 2 + 3 + … + n

Сигма является мощным инструментом в математике, позволяющим компактно записывать сложные выражения и суммы, а также упрощать вычисления. Она широко применяется в различных областях, включая физику, экономику и статистику, где требуется суммирование большого количества значений.

В данной статье мы более подробно рассмотрим использование символа сигмы в математике и предоставим примеры его применения для лучшего понимания.

Сигма в математике: суть и назначение

Назначение сигмы состоит в том, чтобы указывать начальное значение переменной, конечное значение переменной и выражение, которое необходимо просуммировать. Например, с помощью сигмы можно записать сумму всех чисел от 1 до 10 следующим образом:

Σ(n=1 to 10) n = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

Также сигма может быть использована для записи более сложных выражений. Например, сумма квадратов всех чисел от 1 до 5 может быть записана следующим образом:

Σ(n=1 to 5) n^2 = 1^2 + 2^2 + 3^2 + 4^2 + 5^2

Сигма является удобным инструментом для работы с суммами в математике и находит применение в различных областях, таких как алгебра, анализ, теория вероятностей и статистика.

Что такое сигма и для чего она используется?

Сигма может быть использована для записи суммы последовательности чисел или выражений. В таком случае символ сигма ставится перед формулой, которая задает общее правило для слагаемых, и нижний и верхний индексы указывают начало и конец суммирования соответственно. Например, если необходимо записать сумму всех чисел от 1 до 5, можно использовать следующую формулу:

Σ(i, 1, 5) i

Здесь символ сигма стоит перед переменной i, которая пробегает значения от 1 до 5. Суммируются все значения переменной i, а результат записывается после символа сигма.

Также символ сигма может использоваться для записи суммы бесконечного числа слагаемых. В этом случае нижний индекс обычно равен 1, а верхний индекс указывает бесконечность. Например, сумма всех чисел от 1 до бесконечности может быть записана следующим образом:

Σ(i, 1, ∞) i

Символ сигма является мощным инструментом в математике, упрощая запись сложных сумм и позволяя компактно представлять большие объемы данных.

Основные характеристики сигмы

Основные характеристики сигмы включают следующее:

1. Сумма элементов: Сигма используется для обозначения суммы ряда элементов. Например, выражение Σxi означает суммирование всех элементов xi в ряду.

2. Диапазон суммирования: Под сигмой обычно указывается диапазон значений, для которых выполняется суммирование. Например, выражение Σni=1xi означает суммирование всех элементов xi от i=1 до i=n.

3. Индексы: Сигма может иметь индексы, которые указывают порядок или номер элемента в ряду. Например, выражение Σni=1xi означает суммирование всех элементов xi от i=1 до i=n, где i является индексом.

Сигма является важным инструментом для работы с суммами в математике и может быть использована для решения различных задач, связанных с суммированием элементов.

Как понять математическое выражение со знаком сигма?

В математике знак сигма (Σ) используется для обозначения суммы. Он указывает, что необходимо просуммировать все значения выражения, которое находится рядом с сигмой. Выражение внутри сигмы может быть зависимым от переменной (обычно называемой индексом суммы), которая принимает различные значения в определенном диапазоне.

Чтобы понять, как интерпретировать выражение со знаком сигма, важно понимать его структуру и содержание. Обычно выражение со знаком сигма записывается в следующем виде:

Σ(выражение, начальное значение, конечное значение)

Выражение указывает, что мы собираемся суммировать. Начальное значение и конечное значение определяют диапазон значений, которые должны принимать переменная (индекс суммы).

Например, рассмотрим следующее выражение:

Σ(2n, 1, 5)

Здесь выражение 2n указывает, что мы будем удваивать переменную n. Начальное значение равно 1, а конечное значение равно 5. Суммирование этого выражения приведет к следующему результату:

(2 * 1) + (2 * 2) + (2 * 3) + (2 * 4) + (2 * 5) = 30

Таким образом, сумма выражения 2n для n от 1 до 5 равна 30.

Математический знак сигма является мощным инструментом для работы с большими суммами и рядами. Он позволяет нам компактно записывать сложные выражения и проводить их вычисления. Понимание структуры и интерпретации выражений со знаком сигма поможет вам разобраться с такими математическими конструкциями и использовать их в своей работе.

Примеры использования сигмы в математике

Пример 1:

Допустим, у нас есть последовательность чисел: 1, 2, 3, 4, 5. Чтобы вычислить сумму этих чисел, мы можем использовать сигму следующим образом:

ВыражениеЗначение

Σi	1 + 2 + 3 + 4 + 5 = 15

Таким образом, сигма позволяет нам компактно записать и вычислить сумму данной последовательности чисел.

Пример 2:

Предположим, у нас есть последовательность чисел: 2, 4, 6, 8, 10. Мы хотим вычислить сумму квадратов каждого числа в данной последовательности. С помощью сигмы это можно записать следующим образом:

ВыражениеЗначение

Σ(i^2)

2^2 + 4^2 + 6^2 + 8^2 + 10^2 = 4 + 16 + 36 + 64 + 100 = 220

Таким образом, сигма позволяет нам вычислить сумму квадратов чисел в данной последовательности.

Пример 3:

Допустим, у нас есть последовательность чисел: 1, 3, 5, 7, 9. Нам нужно вычислить сумму квадратов нечетных чисел в данной последовательности. С помощью сигмы это можно записать следующим образом:

ВыражениеЗначение

Σ((2i-1)^2)

(2*1-1)^2 + (2*2-1)^2 + (2*3-1)^2 + (2*4-1)^2 + (2*5-1)^2 = 1 + 9 + 25 + 49 + 81 = 165

Таким образом, сигма позволяет нам вычислить сумму квадратов нечетных чисел в данной последовательности.

Сигма и сумма: в чем разница?

Символ сигма, обозначаемый греческой буквой Σ, используется для записи суммы ряда чисел в более компактной форме. Он состоит из символа сигма снизу и сверху расположенных индексов, которые указывают начальное и конечное значение переменной, по которой происходит суммирование. Например, сумма всех чисел от 1 до 5 может быть записана как Σn от 1 до 5, где n — переменная, которая принимает значения от 1 до 5.

Символ суммы, обозначаемый латинской буквой S, также используется для записи суммы ряда чисел. Однако, в отличие от сигмы, он не имеет индексов и не указывает на переменную, по которой происходит суммирование. Например, сумма всех чисел от 1 до 5 может быть записана как S, но без указания переменной n.

Таким образом, разница между символом сигма и символом суммы заключается в их форме записи и возможности указания переменной, по которой происходит суммирование. Сигма предоставляет более информативную запись, позволяя указать переменную и её диапазон, в то время как сумма просто обозначает наличие суммы ряда чисел без указания переменной.

Сигма и произведение: как они связаны?

Сигма-символ используется для указания суммы чисел или выражений, записанных в виде последовательности. Он имеет следующий вид:

Σ i=1 ai

Здесь ai — это элементы последовательности, а i — переменная, принимающая значения от 1 до n, где n — количество элементов в последовательности.

Произведение-символ используется для указания умножения чисел или выражений, записанных в виде последовательности. Он имеет следующий вид:

∏ i=1 ai

Здесь ai — это элементы последовательности, а i — переменная, принимающая значения от 1 до n.

Сигма и произведение имеют много общих свойств. Например, оба символа могут быть использованы для записи суммы или произведения последовательности чисел. Они также могут быть использованы для указания границ суммирования или умножения.

В заключение, сигма и произведение — это два важных символа в математике, которые используются для записи суммы и произведения последовательностей чисел. Они имеют много общих черт и могут быть использованы в различных математических выражениях.

История возникновения и развития сигмы

В древнегреческой математике «сигма» использовалась как символ для обозначения суммы ряда. Это значит, что если у нас есть последовательность чисел, мы можем записать их сумму с помощью символа «сигма».

Однако, самое широкое применение символ «сигма» получил в математической нотации, которая была разработана Леонардом Эйлером в XVIII веке. Эйлер ввел символ «сигма» для обозначения суммы в формуле, что сделало его незаменимым инструментом в математике.

В современной математике символ «сигма» широко используется для записи сумм и последовательностей. Он помогает компактно и эффективно обозначать сложные математические конструкции и упрощает запись формул. Без символа «сигма» математические выражения могли бы быть гораздо более громоздкими и трудными для понимания.

Вопрос-ответ:

Что такое сигма в математике?

Символ сигма в математике обозначает сумму последовательности чисел. Он используется для записи суммы большого количества чисел в более компактной форме.

Как записывается сигма в математике?

Символ сигма записывается как заглавная греческая буква «Σ». Он ставится перед выражением, которое нужно просуммировать, и нижним и верхним индексами, которые указывают диапазон суммирования.

Как использовать символ сигма для суммирования чисел?

Для суммирования чисел с помощью символа сигма, нужно указать диапазон суммирования нижним и верхним индексами. Например, сумма чисел от 1 до 5 записывается как «Σ(i=1 to 5) i».

Какие примеры суммирования чисел с использованием символа сигма?

Примеры суммирования чисел с использованием символа сигма могут быть следующими: сумма первых 10 натуральных чисел — «Σ(i=1 to 10) i», сумма квадратов чисел от 1 до 5 — «Σ(i=1 to 5) i^2», сумма всех чисел из заданной последовательности и т.д.

Можно ли использовать символ сигма для суммирования бесконечных последовательностей?

Да, символ сигма можно использовать для суммирования бесконечных последовательностей, если эта последовательность имеет определенную формулу или закономерность. Например, сумма бесконечной геометрической прогрессии может быть записана с помощью символа сигма.

Что такое сигма в математике?

Сигма (σ) в математике обозначает сумму ряда или последовательности чисел. Это символ используется для обозначения суммы всех элементов в некотором наборе чисел.

Как использовать сигму в математике?

Чтобы использовать сигму в математике, нужно указать нижнюю и верхнюю границы суммирования. Например, сумма всех чисел от 1 до 5 будет выглядеть как σ(1, 5), а сумма всех элементов в массиве a будет обозначаться как σ(a[1], a[n]).

Видео по теме: