Что в математике обозначает греческая буква сигма 5
Содержимое
- 1 Что в математике обозначает греческая буква сигма 5
- 1.1 Греческая буква сигма в математике: основное значение и применение
- 1.2 Значение греческой буквы сигма в математике
- 1.3 Роль сигмы в математических формулах
- 1.4 Сигма как обозначение суммы
- 1.5 Применение сигмы в статистике
- 1.6 Сигма в анализе рядов и последовательностей
- 1.7 Сигма в теории вероятностей
- 1.8 Использование сигмы в дифференциальной геометрии
- 1.9 Применение сигмы в физике и инженерии
- 1.10 Вопрос-ответ:
- 1.10.0.1 Зачем нужна греческая буква сигма в математике?
- 1.10.0.2 Как записывается сумма с использованием греческой буквы сигма?
- 1.10.0.3 Какие другие обозначения существуют для суммы в математике?
- 1.10.0.4 Можно ли использовать греческую букву сигма для обозначения других операций, кроме суммирования?
- 1.11 Видео по теме:
Греческая буква сигма 5 в математике используется для обозначения суммы элементов последовательности или ряда. Узнайте, как применяется эта буква и как она связана с понятием суммирования в математике.
Греческая буква сигма (σ) в математике имеет особое значение и широко используется для обозначения суммы. Сигма в математике является специальным символом, который позволяет компактно записывать большие суммы и упрощает вычисления.
Сигма используется для обозначения суммы ряда чисел или выражений. Например, если у нас есть последовательность чисел a1, a2, a3, …, an, то сумма этих чисел может быть записана как ∑ai, где i принимает значения от 1 до n. Такая запись позволяет наглядно указать, что речь идет о сумме ряда чисел.
Использование сигмы в математике также позволяет записывать сложные суммы и выражения более компактно. Например, сумма всех натуральных чисел от 1 до 100 может быть записана как ∑i, где i принимает значения от 1 до 100. Такая запись является более краткой и удобной для анализа и вычислений.
Греческая буква сигма в математике имеет особое значение и является ключевым символом для обозначения суммы ряда чисел или выражений. Её использование позволяет записывать суммы более компактно и удобно, облегчая анализ и вычисления. Сигма является неотъемлемой частью математической нотации и важным инструментом для работы с суммами.
Греческая буква сигма в математике: основное значение и применение
Буква сигма может использоваться для обозначения суммы ряда или последовательности. Например, с помощью сигмы можно записать сумму первых n членов арифметической или геометрической прогрессии. Также с ее помощью можно записать сумму элементов массива или результат некоторой операции над последовательностью чисел.
В математических формулах буква сигма может использоваться в следующем виде:
- Σx — сумма значений x;
- Σf(x) — сумма значений функции f(x);
- Σa_k — сумма элементов последовательности a_k;
Также сигма может быть использована для записи бесконечных сумм, которые в математике называются рядами. Например, с помощью сигмы можно записать сумму всех натуральных чисел или сумму ряда гармонического ряда.
В заключение можно сказать, что греческая буква сигма является важным символом в математике, который используется для обозначения суммирования и записи сумм рядов и последовательностей. Она помогает упростить и компактно записать сложные математические выражения, а также улучшает читаемость и понимание математических формул и уравнений.
Значение греческой буквы сигма в математике
Одним из наиболее распространенных использований буквы сигма в математике является обозначение суммы. Когда сигма используется в этом контексте, она обозначает сумму всех элементов в некотором ряде или последовательности. Например, сигма может быть использована для записи суммы всех чисел от 1 до 10:
σ i = 1^10 i
Эта запись означает, что нужно просуммировать все числа от 1 до 10, то есть 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55.
Сигма также может использоваться для обозначения суммы бесконечного ряда или последовательности. В этом случае она может представлять бесконечную сумму всех членов ряда. Например, сигма может быть использована для записи суммы всех обратных квадратов чисел:
σ i = 1^∞ 1/i^2
Эта запись означает, что нужно просуммировать все обратные квадраты чисел, начиная с 1 и до бесконечности. Такая сумма известна как гармонический ряд и имеет конечное значение π^2/6.
Кроме сумм, буква сигма может использоваться для обозначения других математических операций, таких как произведение (пи-произведение), интегралы и дифференцирование. Однако сумма является одним из наиболее распространенных и широко используемых значений для буквы сигма в математике.
Роль сигмы в математических формулах
Греческая буква сигма (σ) играет важную роль в математике и широко используется в математических формулах. Она обозначает сумму последовательности чисел или выражений.
Символ сигмы (σ) часто используется для записи суммы от i=1 до n в виде ∑ (нижняя граница i=1, верхняя граница n) xi, где xi — элементы последовательности. Такая запись означает, что нужно сложить все элементы последовательности от i=1 до n.
Например, если дана последовательность чисел 1, 2, 3, 4, 5, символ сигма (σ) позволяет записать сумму всех этих чисел в виде ∑ (нижняя граница i=1, верхняя граница 5) xi = 1 + 2 + 3 + 4 + 5 = 15.
Кроме того, сигма (σ) также может использоваться для записи суммы с условием. Например, если дана последовательность чисел 1, 2, 3, 4, 5, и нужно найти сумму только четных чисел, можно записать это в виде ∑ (нижняя граница i=1, верхняя граница 5; условие xi четное) xi = 2 + 4 = 6.
Таким образом, сигма (σ) является мощным инструментом для записи и вычисления суммы последовательностей в математических формулах. Она позволяет сократить запись и сделать ее более компактной и понятной.
Сигма как обозначение суммы

Греческая буква сигма (Σ) широко используется в математике для обозначения суммы. Этот символ используется для указания суммы ряда чисел или выражений.
Обычно сигма размещается перед выражением, которое указывает на переменную, а под ней размещаются верхний и нижний пределы суммирования. Например, запись ∑i=1n ai означает сумму элементов a1, a2, a3, …, an.
Применение сигмы в математике позволяет сократить запись длинных сумм и сделать ее более компактной и удобной для чтения. Также сигма позволяет совмещать различные операции суммирования и использовать их в различных контекстах.
Сигма имеет множество применений в различных областях математики, включая алгебру, анализ, комбинаторику и статистику. Она является одним из наиболее распространенных математических символов и широко используется в научных и инженерных расчетах.
Использование сигмы в математике требует понимания контекста и правильного определения переменных и пределов суммирования. Это позволяет более точно и компактно записывать математические выражения и проводить сложные вычисления.
Применение сигмы в статистике
Символ сигмы часто встречается в формулах и уравнениях, связанных со статистикой. Он указывает, что нужно вычислить сумму разностей между каждым значением и средним значением, возведенными в квадрат, после чего найти среднее арифметическое этих квадратов. Затем выполняется квадратный корень от полученного значения, что и дает стандартное отклонение.
Использование сигмы в статистике позволяет оценить, насколько хорошо данные согласуются с моделью или теоретическими ожиданиями. Большое значение стандартного отклонения указывает на большой разброс данных и низкую предсказуемость, тогда как маленькое значение свидетельствует о малом разбросе и высокой предсказуемости.
В статистических расчетах сигма может быть записана как символ, так и в числовом значении. Например, σ = 3 означает, что стандартное отклонение равно 3. Это позволяет упростить запись и обозначение в формулах, делая их более компактными и легкими для понимания.
Таким образом, применение сигмы в статистике позволяет оценить и измерить разброс значений в наборе данных, что является важным инструментом для анализа и интерпретации статистической информации.
Сигма в анализе рядов и последовательностей

Греческая буква сигма (Σ) имеет особое значение в математике, особенно в анализе рядов и последовательностей. Она обозначает сумму элементов ряда или последовательности. Чтобы использовать сигму, нужно указать начальное значение индекса, затем верхнюю границу суммирования и выражение, определяющее каждый элемент ряда или последовательности, внутри сигмы.
Символ сигмы позволяет компактно записывать суммы большого количества элементов. Например, рассмотрим ряд чисел от 1 до 10. Мы можем записать его с использованием сигмы следующим образом:
Σn = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
В данном случае, n является индексом, который принимает значения от 1 до 10, а Σn обозначает сумму всех чисел от 1 до 10.
С помощью сигмы можно также записывать общую формулу суммы элементов ряда или последовательности. Например, сумма первых n натуральных чисел может быть записана следующим образом:
Σk = 1 + 2 + 3 + … + n
Здесь k является индексом, который принимает значения от 1 до n, а Σk обозначает сумму всех чисел от 1 до n.
Сигма является мощным инструментом для суммирования элементов рядов и последовательностей, и ее использование позволяет компактно записывать сложные выражения и проводить различные операции с суммами.
Сигма в теории вероятностей

Сигма используется в формулах для расчета стандартного отклонения и позволяет оценить, насколько точные и предсказуемые значения может дать данная случайная величина. Чем меньше значение стандартного отклонения, тем более сгруппированы значения случайной величины вокруг ее среднего значения.
Стандартное отклонение является важной характеристикой в теории вероятностей, поскольку позволяет определить форму и тип распределения случайной величины. Например, нормальное распределение имеет известные значения среднего и стандартного отклонения, что делает его одним из самых изучаемых и применяемых в статистике и эконометрике.
Использование греческой буквы сигма для обозначения стандартного отклонения в теории вероятностей позволяет унифицировать обозначения и предоставить стандартный символ для данной концепции. Благодаря этому, сигма легко узнаваема и широко распространена в академической литературе, научных статьях и математических формулах, связанных с теорией вероятностей и статистикой.
Использование сигмы в дифференциальной геометрии
В дифференциальной геометрии сигма используется для обозначения суммирования коэффициентов в разложении функций в ряд Тейлора. Ряд Тейлора представляет функцию в виде бесконечной суммы мономов, каждый из которых имеет свой коэффициент. Сигма позволяет компактно записать эту сумму и указать границы суммирования.
Например, если у нас есть функция f(x), которую мы хотим разложить в ряд Тейлора в окрестности точки a, то с помощью сигмы запись будет выглядеть следующим образом:
f(x) = Σn=0∞ an(x-a)n
Здесь an — это коэффициенты разложения, (x-a)n — мономы, а границы суммирования n=0 и ∞ указывают, что мы складываем все значения от нуля до бесконечности.
Использование сигмы позволяет более компактно записывать сложные математические выражения и упрощает их анализ и решение. Она является одним из важных инструментов в дифференциальной геометрии и помогает упростить вычисления и изучение свойств функций.
Применение сигмы в физике и инженерии
Греческая буква сигма (σ) имеет широкое применение в физике и инженерии. Она используется для обозначения суммы ряда или последовательности чисел, а также для обозначения стандартного отклонения в статистике.
В физике сигма используется для обозначения суммы величин, например, в силовых формулах или законах сохранения. Она позволяет суммировать все значения измеряемой величины, представленные в виде ряда или последовательности. Таким образом, сигма упрощает математические вычисления и помогает анализировать результаты экспериментов.
В инженерии сигма часто используется для обозначения суммируемых величин, например, в формулах для расчета сопротивления материалов или электрических цепей. Она также может использоваться для обозначения суммы приведенных потерь или суммы всех элементов в системе.
Кроме того, сигма может использоваться для обозначения стандартного отклонения в статистике. Стандартное отклонение позволяет измерить разброс значений относительно среднего значения. С помощью сигмы можно выразить стандартное отклонение и проводить анализ данных, например, для определения точности измерений или оценки рисков.
Примеры применения сигмы в физике и инженерии:
| 1. Формула силы: F = σ Fi |
| 2. Закон сохранения энергии: E = σ Ei |
| 3. Расчет сопротивления материалов: R = σ Ri |
| 4. Формула для суммы приведенных потерь: σL = L1 + L2 + … + Ln |
| 5. Вычисление стандартного отклонения: σ = sqrt((Σ(x — μ)2)/n) |
Все эти примеры демонстрируют важность и широкое применение греческой буквы сигма в физике и инженерии. Она помогает упростить математические вычисления, обозначить суммы и стандартное отклонение, а также проводить анализ полученных данных.
Вопрос-ответ:
Зачем нужна греческая буква сигма в математике?
Греческая буква сигма используется в математике для обозначения суммы последовательности чисел. Она позволяет компактно записать формулу для вычисления суммы и упростить выражение.
Как записывается сумма с использованием греческой буквы сигма?
Сумма с использованием греческой буквы сигма записывается следующим образом: сигма, затем индекс, который указывает начальное значение переменной, и верхний предел суммирования, после чего идет выражение, которое суммируется. Например, сумма чисел от 1 до 10 записывается как сигма(i=1,10)i.
Какие другие обозначения существуют для суммы в математике?
Помимо греческой буквы сигма, для обозначения суммы в математике также используются символы «сумма» и «E». Например, сумма чисел от 1 до 10 также может быть записана как сумма(i=1,10)i или E(i=1,10)i.
Можно ли использовать греческую букву сигма для обозначения других операций, кроме суммирования?
Греческая буква сигма применяется в математике именно для обозначения суммирования. Однако, в других науках и областях знаний, сигма может использоваться для обозначения различных величин и операций, например, в физике для обозначения поверхностного натяжения или в статистике для обозначения стандартного отклонения.

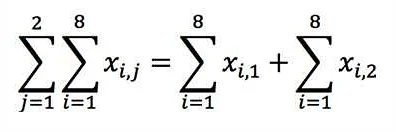


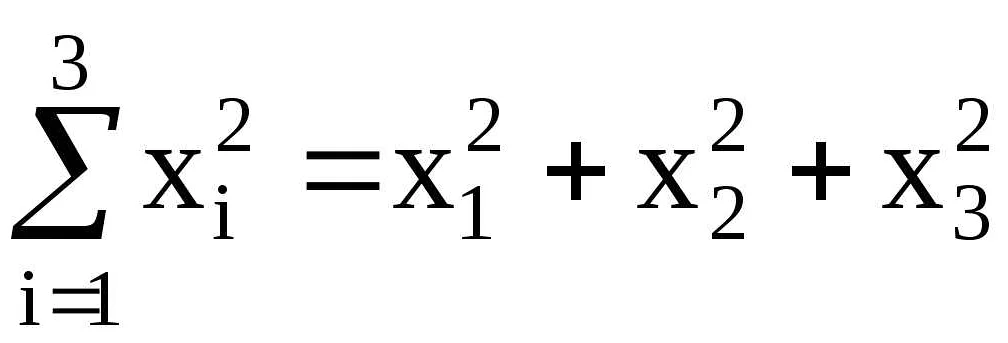
Сигма, греческая буква, используется в математике для обозначения суммы. Она помогает нам суммировать большие и малые числа, что делает ее очень полезной в решении различных задач. Например, если у нас есть последовательность чисел, мы можем использовать сигму, чтобы найти их сумму. Это особенно полезно, когда у нас есть большое количество элементов в последовательности и мы хотим найти их общую сумму без необходимости перечисления каждого числа отдельно. Сигма также используется для обозначения суммы вероятностей или функций в статистике. Она позволяет нам суммировать вероятности или значения функций для различных событий или значений переменных. Это помогает нам анализировать данные и делать выводы на основе статистических методов. Таким образом, греческая буква сигма играет важную роль в математике, облегчая суммирование элементов последовательностей и анализ данных. Она является неотъемлемой частью математической нотации и помогает нам лучше понять и решать различные задачи.
Греческая буква сигма в математике имеет особое значение и широко используется для обозначения суммы. В формулах и уравнениях она указывает на необходимость сложения ряда чисел или выражений. Например, если есть последовательность чисел, то с помощью сигмы можно указать, что нужно сложить все эти числа вместе. Сигма представляет собой мощный инструмент, который позволяет компактно записывать сложные математические выражения. Она позволяет сократить объем записи и сделать ее более ясной и понятной. Кроме того, сигма используется для обозначения суммы итераций в различных алгоритмах и рядах чисел. Это может быть полезно, например, в статистике, когда нужно вычислить сумму большого количества значений. Таким образом, греческая буква сигма играет важную роль в математике, обозначая сумму ряда чисел или итераций. Она помогает упростить запись и сделать ее более понятной. Использование сигмы позволяет увидеть общий паттерн и структуру данных, что является важным инструментом для математиков и ученых.
Греческая буква сигма в математике играет важную роль, используется для обозначения суммирования. Она отлично помогает упростить запись и вычисление больших сумм. Благодаря сигме, мы можем удобно и компактно записывать сложные формулы и вычисления. Например, если нам нужно сложить все числа от 1 до n, мы можем записать это как сумму от i=1 до n. Вот где сигма приходит на помощь — она позволяет нам указать диапазон суммирования. Также греческая буква сигма используется для обозначения сигма-алгебры в теории вероятности и математической статистике. Она помогает определить множество событий, которые мы можем рассматривать. В целом, сигма является одним из ключевых символов в математике, который помогает упростить запись и вычисления.