Сигма в математике как решать
Содержимое
- 1 Сигма в математике как решать
Узнайте, как решать задачи с использованием сигмы в математике. Понимайте, как применять сумму сигмы для нахождения общей суммы числового ряда. Получите полезные советы и примеры для эффективного использования сигмы в решении математических задач.
Сигма (символ Σ) – это один из наиболее используемых символов в математике, который представляет собой большую греческую букву «сигма». В математической нотации сигма обозначает сумму чисел или функций. Математики используют сигму для представления сложения последовательности чисел или результатов функций. Сигма позволяет нам записать сложение большого количества чисел или результатов функций более компактно и элегантно.
Сигма имеет свои правила использования. Перед символом сигма обычно указываются начальное значение переменной, а после символа сигма – конечное значение переменной. Затем внутри символа сигма записываются выражения, которые нужно сложить. Например, сумма всех целых чисел от 1 до 10 может быть записана следующим образом: Σ i=1 до 10 (i).
Использование сигмы может быть очень полезно для решения различных задач. Например, сигма позволяет легко вычислить сумму арифметической или геометрической прогрессии, а также сумму ряда чисел, следующих определенному закону. Кроме того, сигма может быть использована для вычисления суммы значений функции для некоторого диапазона значений переменной. Знание правил использования сигмы позволяет эффективно решать множество задач в различных областях математики.
Сигма в математике: основные понятия
Символ сигма (Σ) в математике обозначает сумму последовательности чисел. Этот символ широко используется для удобства записи и обозначения суммы большого количества чисел.
Сигма-нотация позволяет компактно записывать суммы и исследовать их свойства. Символ Σ ставится перед выражением, которое нужно просуммировать, а сверху и снизу указываются значения, на которых меняется переменная, по которой происходит суммирование.
Сумма, обозначенная символом сигма, может быть представлена в виде таблицы. В левой колонке таблицы указываются значения переменной, а в правой колонке — значения выражения, которое нужно просуммировать. Затем, результаты суммирования суммируются и записываются внизу таблицы.
Значение переменнойЗначение выражения
| x1 | f(x1) |
| x2 | f(x2) |
| x3 | f(x3) |
| … | … |
| xn | f(xn) |
| Σ | f(xi) |
В таблице выше, значения переменной x1, x2, …, xn меняются от одного до другого, а выражение f(xi) — это функция, зависящая от переменной xi. Результатом суммирования является сумма значений выражения f(xi) для всех значений переменной xi.
Символ сигма в математике также может быть использован для записи формул, включающих суммы, и для обозначения бесконечных сумм, которые называются рядами.
Определение сигмы
Сигма может использоваться с индексами, которые указывают на начало и конец суммирования. Например, сумма чисел от 1 до 5 может быть записана как:
Σi=15 i = 1 + 2 + 3 + 4 + 5 = 15
Здесь индекс i указывает на переменную, которая меняется от 1 до 5. Символы снизу и сверху от сигмы обозначают начальное и конечное значение индекса соответственно.
Таким образом, сигма позволяет компактно записывать суммы и делает их более понятными и удобными для анализа и решения математических задач.
Использование сигмы в суммах
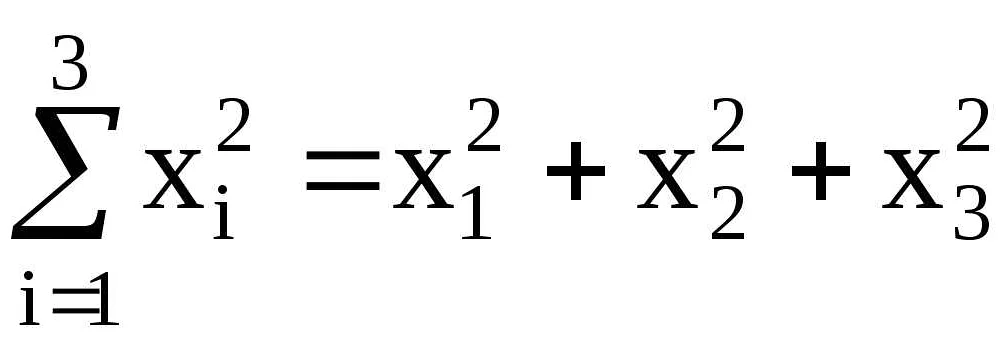
Сигма (Σ) в математике используется для обозначения суммы. Она позволяет компактно записывать большие суммы и удобно их вычислять. Сигма ставится перед выражением, которое нужно суммировать.
Общий вид записи сигмы выглядит следующим образом:
Σ f(i)
где f(i) — выражение, которое нужно суммировать, а переменная i принимает значения от некоторого начального значения до некоторого конечного значения.
При вычислении суммы сигмы сначала подставляются значения переменной i в выражение f(i), а затем полученные значения складываются.
Например, сумма первых 5 натуральных чисел может быть записана с помощью сигмы:
Σ i
где i принимает значения от 1 до 5. Вычислим данную сумму:
Σ i = 1 + 2 + 3 + 4 + 5 = 15
Таким образом, сигма позволяет удобно записывать и вычислять суммы, что делает ее полезным инструментом в математике.
Свойства сигмы
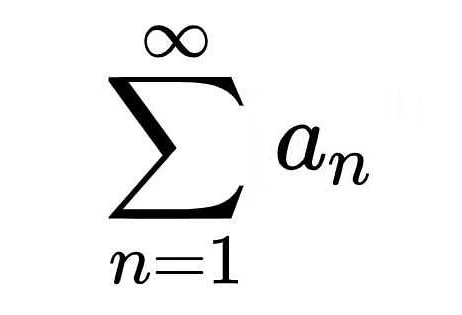
1. Свойство линейности: сумма двух сигм равна сигме суммы. То есть, если у нас есть две сигмы: ∑i=1n ai и ∑i=1n bi, то их сумма будет равна сигме суммы: ∑i=1n (ai+bi).
2. Свойство разложения: сигму можно разложить на несколько отдельных сигм с помощью свойства линейности. Например, сигму ∑i=1n (ai+bi) можно разложить на две сигмы: ∑i=1n ai и ∑i=1n bi.
3. Свойство постоянного множителя: сигму можно умножить на постоянный множитель, и результат будет равен сумме элементов, умноженных на этот множитель. Например, k∑i=1n ai равно ∑i=1n (kai).
4. Свойство индекса: индекс сигмы можно изменить, и это не повлияет на результат. То есть, ∑i=1n ai равно ∑j=1n aj.
5. Свойство смещения: сигму можно сместить на произвольное количество элементов, и это не повлияет на результат. Например, ∑i=1n ai равно ∑i=2n+1 ai-1.
Применение сигмы в алгебре

В алгебре сигма-нотация (σ-нотация) часто используется для обозначения суммирования элементов последовательности или функции.
Символ сигмы, обозначаемый греческой буквой σ, имеет следующий вид: ∑.
Чтобы указать, какие элементы нужно суммировать, индексы нижнего и верхнего пределов указываются над и под символом сигмы соответственно. Например:
∑k=1n ak = a1 + a2 + a3 + … + an
Это выражение означает суммирование элементов ak от k=1 до k=n.
Сигма-нотация также может использоваться для обозначения суммирования функций:
∑k=1n f(k) = f(1) + f(2) + f(3) + … + f(n)
Здесь f(k) — функция, которую нужно суммировать по значениям k.
Сигма-нотация позволяет компактно записывать сложные выражения, которые включают суммирование. Она также используется для формулирования и доказательства математических теорем и формул.
Сигма и матрицы

Сигма (символ Σ) в математике обычно используется для обозначения суммы. Однако, сигма также может быть использована для работы с матрицами.
Матрицы представляют собой таблицы чисел, разделенных на строки и столбцы. Каждый элемент матрицы обозначается индексом, состоящим из номера строки и номера столбца. Сигма позволяет совершать операции с матрицами, такие как суммирование элементов или перемножение матриц.
Например, сумма элементов матрицы может быть выражена с помощью сигмы следующим образом:
| а11 | а12 | а13 |
| а21 | а22 | а23 |
| а31 | а32 | а33 |
Сумма всех элементов матрицы может быть записана как:
Σi=13Σj=13аij
Это означает, что нужно просуммировать все элементы матрицы, начиная с первого элемента до третьего столбца и третьей строки. Результат этой суммы будет являться числовым значением.
Кроме суммирования, сигма также может использоваться для умножения матриц. Для этого используются две сигмы: одна для указания строк первой матрицы, а другая для указания столбцов второй матрицы. Результатом будет новая матрица, полученная в результате умножения.
В заключение, сигма в математике не только представляет сумму, но также может быть использована для работы с матрицами, позволяя выполнять операции с элементами и структурами данных.
Подсчет сигмы на практике
Для подсчета сигмы на практике нужно следовать нескольким правилам. Во-первых, нужно указать начальное значение индекса (обычно это натуральное число или ноль). Затем нужно указать верхнюю границу суммирования, то есть значение, до которого будет производиться суммирование. Наконец, нужно указать выражение, которое будет суммироваться.
Например, чтобы вычислить сумму чисел от 1 до 5, можно использовать следующую запись: Σi=15 i. Здесь «i=1» — начальное значение индекса, «5» — верхняя граница суммирования, «i» — выражение, которое суммируется. Результатом будет число 15.
Сигма также может быть использована для вычисления суммы выражений. Например, чтобы вычислить сумму квадратов чисел от 1 до 3, можно использовать запись: Σi=13 i2. Результатом будет число 14.
При подсчете сигмы на практике важно учитывать порядок операций. Если в выражении есть скобки, нужно сначала выполнить вычисления внутри скобок, а затем выполнять суммирование.
Таким образом, подсчет сигмы может быть полезным инструментом при решении различных задач в математике. Правильное использование сигмы позволяет эффективно суммировать большие последовательности чисел или выражений и получать точные результаты.
Сигма в дифференциальных уравнениях
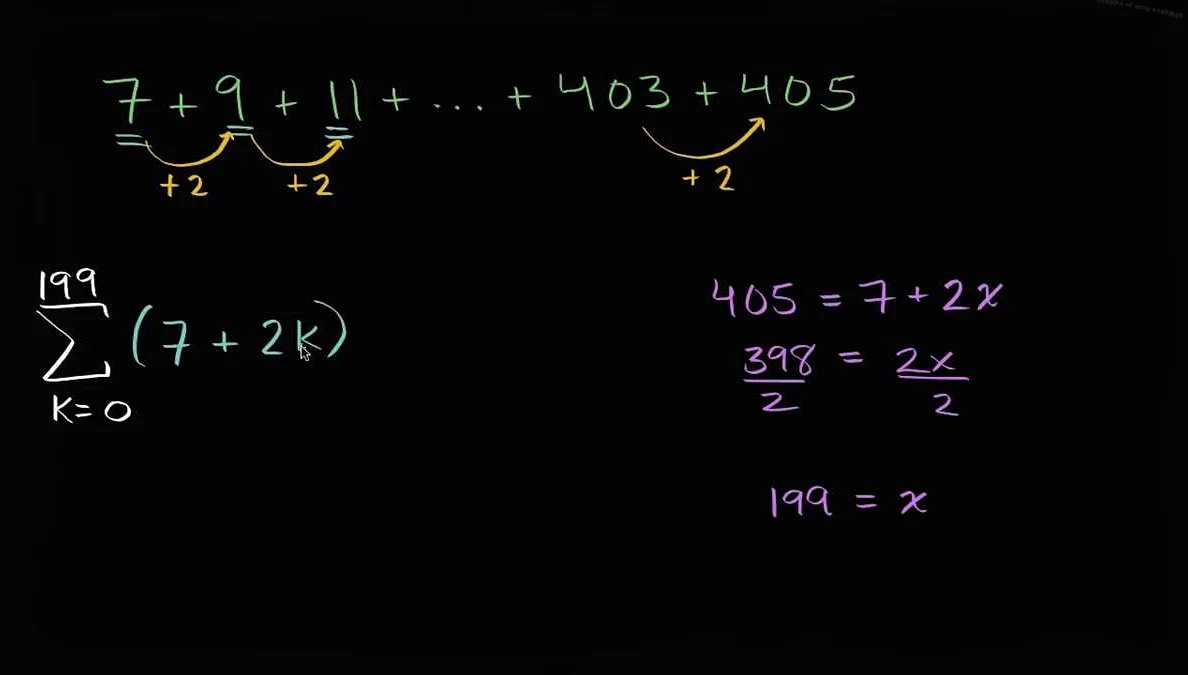
В дифференциальных уравнениях сигма может использоваться для обозначения оператора суммирования в пределах некоторого диапазона значений. Например, рассмотрим дифференциальное уравнение:
dy/dx = Σ(i=1 to n) (a_i * x^i)
В этом уравнении сигма используется для суммирования всех слагаемых, где a_i — коэффициенты, x — переменная, а i — индекс суммирования. Такое использование сигмы позволяет компактно записывать сложные дифференциальные уравнения с большим количеством слагаемых.
Кроме того, сигма может быть использована для обозначения ряда, который представляет собой бесконечную сумму дифференциальных слагаемых. Например, рассмотрим уравнение:
dy/dx = Σ(n=0 to ∞) (a_n * x^n)
Здесь сигма обозначает суммирование всех слагаемых с бесконечным диапазоном значений n. Такое использование сигмы позволяет описывать функции с бесконечным числом слагаемых, что может быть полезно при решении определенных типов дифференциальных уравнений.
Использование сигмы в дифференциальных уравнениях позволяет более компактно записывать сложные математические выражения и упрощает процесс их решения. Однако, для правильного понимания и применения сигмы в дифференциальных уравнениях необходимо иметь хорошее понимание основ математического анализа и дифференциальных уравнений.
ПримерОписание
| dy/dx = Σ(i=1 to n) (a_i * x^i) | Дифференциальное уравнение с сигмой в пределах от 1 до n |
| dy/dx = Σ(n=0 to ∞) (a_n * x^n) | Дифференциальное уравнение с сигмой и бесконечным диапазоном значений |
Вопрос-ответ:
Что такое символ сигма в математике?
Символ сигма в математике обозначает сумму последовательности чисел.
Какие правила применяются при использовании символа сигма?
При использовании символа сигма применяются правила выражения и сокращения суммы, правило индексации и правило раскрытия скобок.
Как можно решать задачи, связанные с символом сигма?
Для решения задач, связанных с символом сигма, можно использовать методы математического анализа, комбинаторики и алгебры, а также применять различные тождества и формулы.
Какие способы решения существуют для задач, связанных с символом сигма?
Существуют различные способы решения задач, связанных с символом сигма, такие как метод индукции, метод подстановки, метод замены переменных, метод приведения к общему знаменателю и другие.
Задачи с использованием сигмы
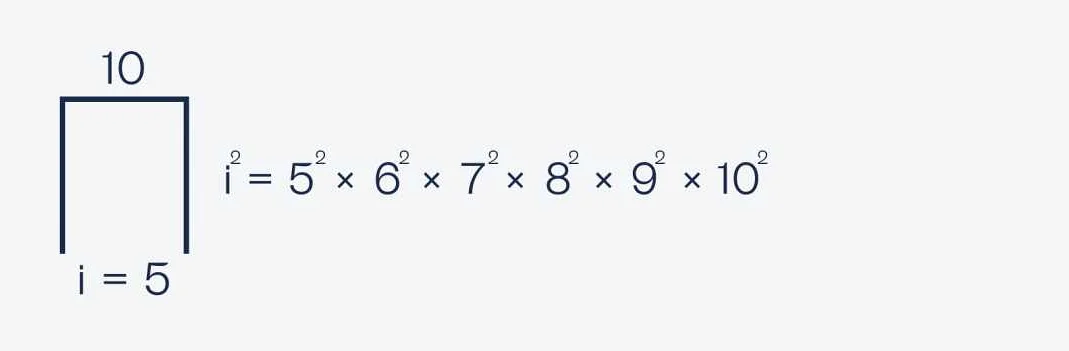
Вот несколько примеров задач, в которых можно использовать сигму:
- Найти сумму первых n натуральных чисел. Для этого можно использовать формулу: ∑i=1n i = n(n+1)/2.
- Вычислить сумму квадратов первых n натуральных чисел. Формула будет выглядеть так: ∑i=1n i2 = n(n+1)(2n+1)/6.
- Найти сумму элементов арифметической прогрессии. Для этого используется формула: ∑i=1n (a + (i-1)d) = n(2a + (n-1)d)/2, где a — первый член прогрессии, d — разность прогрессии.
- Вычислить сумму элементов геометрической прогрессии. Формула будет иметь вид: ∑i=0n a0 * ri = a0(1 — rn+1)/(1 — r), где a0 — первый член прогрессии, r — знаменатель прогрессии.
Все эти задачи можно решать как аналитически, так и с использованием сигмы. Использование сигмы облегчает и упрощает запись и вычисления, особенно в случае, когда нужно найти сумму большого количества чисел.
Таким образом, сигма является мощным инструментом в математике, который помогает решать задачи, связанные с суммированием чисел и вычислением сумм рядов.
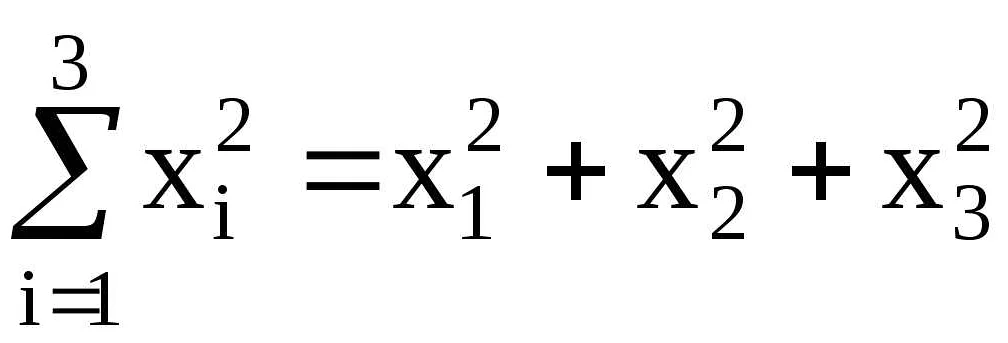

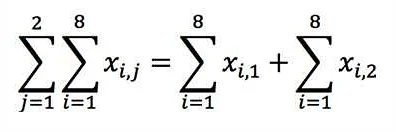


В статье очень понятно и подробно объяснено, что такое сигма в математике и как с ней работать. Я всегда считала, что эта буква имеет какое-то важное значение, но никогда не знала, как ее использовать. Теперь я понимаю, что сигма обозначает сумму элементов ряда или последовательности, и это очень удобно для упрощения сложных вычислений. Также мне понравилась информация о различных правилах работы с сигмой, например, о том, что можно выносить константы за знак суммы или использовать индексы для обозначения переменных. Теперь я буду гораздо увереннее в решении задач на сигму и смогу справиться с ними легче и быстрее. Спасибо автору за такую полезную и понятную статью!
Статья очень информативная и понятная. Я уже давно интересуюсь математикой, и особенно мне нравится работа с сигмой. В статье полно примеров и объяснений, которые помогают лучше разобраться в правилах и способах решения задач с использованием этого символа. Очень удобно, что авторы статьи также предоставили ссылки на дополнительные материалы и ресурсы, где можно еще больше узнать о сигме и ее применении. Благодаря этой статье, я теперь лучше понимаю, как использовать сигму в своих математических расчетах и задачах. Очень рекомендую всем, кто интересуется математикой, ознакомиться с этой статьей!