Что такое см3 в математике

См3 (кубический сантиметр) — это единица объема в математике, равная объему куба со стороной длиной один сантиметр. Узнайте, как использовать см3 в решении задач по геометрии и физике.

См³ (кубический сантиметр) — это единица объема в трехмерной геометрии и математике. Она представляет собой объем, занимаемый кубом со стороной длиной 1 сантиметр. См³ широко используется для измерения объемов твердых тел, жидкостей и газов в научных и инженерных расчетах.

Для вычисления объема кубического тела или контейнера можно воспользоваться формулой: объем = длина × ширина × высота. Если все измерения даны в сантиметрах, то единицей измерения объема будет см³. Например, если у нас есть куб со стороной длиной 5 сантиметров, то его объем будет равен 5 × 5 × 5 = 125 см³.

См³ также может использоваться для измерения объема жидкостей, например, в химических экспериментах. Например, если нам нужно измерить объем воды, залитой в пробирку, то мы можем использовать мерную пробирку, помеченную в сантиметрах кубического объема. Например, если в пробирку помещается 50 см³ воды, это означает, что объем воды равен 50 см³.

Использование см³ в математике позволяет нам более точно и удобно измерять объемы различных объектов и веществ. Благодаря этой единице измерения нам легче совершать точные расчеты и проводить научные исследования в области геометрии, физики, химии и других наук.

См3 в математике: определение и примеры использования

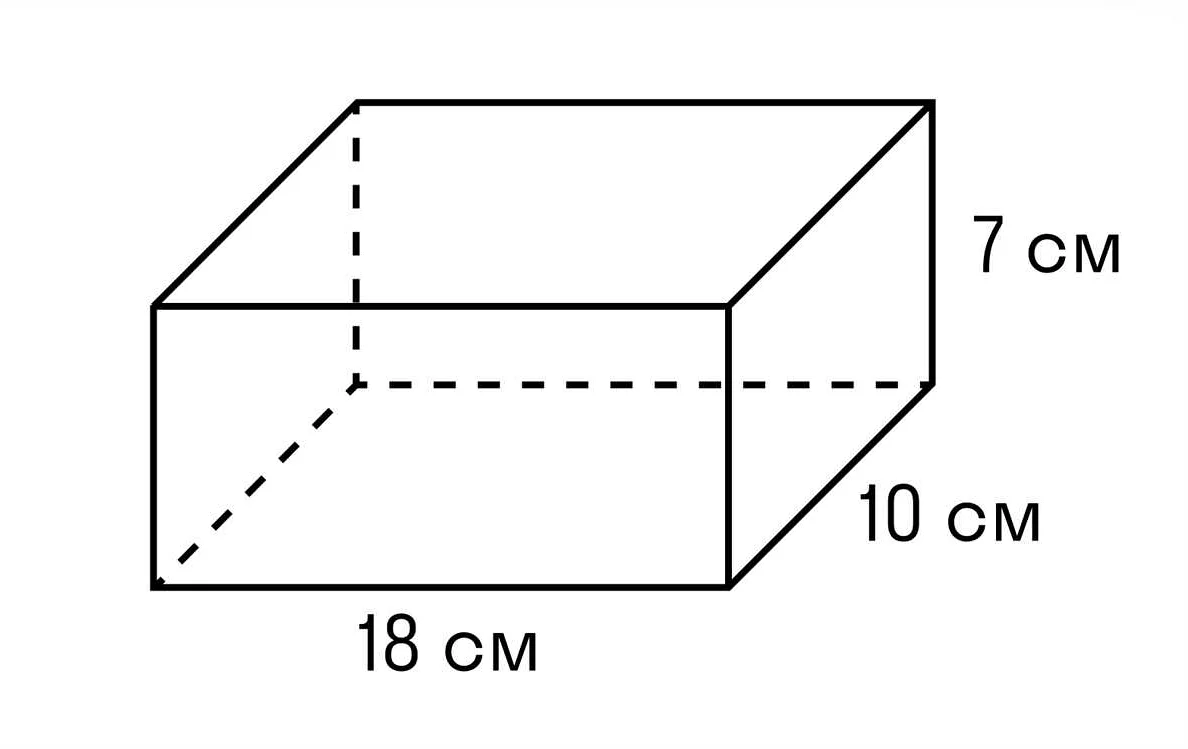
См3 является произведением трех размеров — длины, ширины и высоты — и обозначает объем кубической формы, каждое измерение которой равно одному сантиметру.

Например, если у нас есть параллелепипед со сторонами длиной 2 см, шириной 3 см и высотой 4 см, то его объем будет равен 2 см * 3 см * 4 см = 24 см3.

См3 также используется для измерения объема жидкостей. Например, если у нас есть стакан с жидкостью высотой 10 см и поперечным сечением площадью 5 см2, то объем жидкости в стакане будет равен 10 см * 5 см2 = 50 см3.

Таким образом, см3 предоставляет удобный способ измерения объема различных объектов в математике и науке.

Определение см3 в математике

Для понимания, как использовать см3, рассмотрим пример. Предположим, у нас есть прямоугольный параллелепипед, у которого длина равна 5 сантиметрам, ширина — 3 сантиметра, а высота — 2 сантиметра. Чтобы найти его объем в сантиметрах кубических, необходимо перемножить значения длины, ширины и высоты: 5 см * 3 см * 2 см = 30 см3.

Таким образом, см3 позволяет нам измерять объем объектов в трехмерном пространстве и решать задачи, связанные с геометрией и физикой.

ФормулаПример

См3 = длина * ширина * высота

5 см * 3 см * 2 см = 30 см3

См3 и единицы объема

См3 является частью системы Международной системы единиц (СИ) и широко используется в научных расчетах и инженерных измерениях. Он часто применяется, например, для измерения объема жидкостей или газов, объема твердых тел или массы вещества, если известна их плотность.

См3 можно перевести в другие единицы объема, используя соответствующие коэффициенты. Например, 1 см3 = 0,001 литра или 1 см3 = 0,061 кубического дюйма.

Единицы объема позволяют проводить измерения и расчеты, связанные с объемом предметов, веществ или пространства. Они важны в физике, химии, геометрии и других научных и технических областях.

См3 — это удобная единица объема, позволяющая сравнивать и измерять объемы различных объектов или веществ с высокой точностью.

Как измеряется объем в см3?

Один кубический сантиметр равен объему куба со стороной длиной 1 сантиметр. То есть, если у нас есть куб со стороной длиной 1 сантиметр, то его объем будет равен 1 см3.

Объем можно измерить в см3, используя различные предметы или инструменты, которые имеют известные размеры и геометрические формы. Например, можно использовать кубический контейнер, у которого все стороны равны 1 см. Затем, наполнив этот контейнер до краев, можно определить объем, который будет равен 1 см3.

Также, для измерения объема в см3 можно использовать градуированный цилиндр, шприц или другие объемные измерительные инструменты, которые позволяют точно определить количество жидкости или газа в сантиметрах кубических.

Знание и понимание того, как измеряется объем в см3, является важным для решения различных задач, связанных с геометрией, физикой и другими областями научного знания.

Расчет объема в см3

Расчет объема в см3 осуществляется с помощью формулы:

ФигураФормула расчета объема в см3

Параллелепипед	Объем = Длина x Ширина x Высота
Цилиндр	Объем = Площадь основы x Высота
Сфера	Объем = 4/3 x Пи x Радиус в кубе

Например, если нам известны размеры параллелепипеда — длина, ширина и высота, то мы можем легко вычислить его объем по формуле: объем = Длина x Ширина x Высота.

Аналогично, для цилиндра необходимо знать площадь его основы и высоту, чтобы рассчитать его объем по формуле: объем = Площадь основы x Высота.

Для сферы требуется знать радиус, чтобы рассчитать ее объем по формуле: объем = 4/3 x Пи x Радиус в кубе.

Таким образом, расчет объема в см3 позволяет определить, сколько пространства занимает объект или материал в трехмерном пространстве.

Свойства см3 в математике

Вот некоторые свойства см3:

1. См3 используется для измерения объема тела. Например, если у нас есть параллелепипед со сторонами 5 см, 4 см и 3 см, его объем будет равен 60 см3.
2. См3 можно использовать для измерения объема жидкости. Например, если у нас есть стакан объемом 250 мл, то это эквивалентно 250 см3.
3. См3 можно использовать для измерения объема геометрических фигур, таких как шары, конусы и цилиндры. Например, если у нас есть шар радиусом 2 см, его объем будет равен приблизительно 33,5 см3.
4. См3 можно использовать для измерения объема скульптур и других трехмерных объектов. Например, если у нас есть скульптура высотой 10 см, шириной 5 см и глубиной 3 см, ее объем будет равен 150 см3.

См3 является удобной единицей измерения объема, так как она позволяет точно измерять объемы различных объектов и фигур в трехмерном пространстве.

Примеры использования см3

1. Вычисление объема прямоугольника: если длина, ширина и высота прямоугольника равны 5 см, 3 см и 2 см соответственно, то его объем вычисляется по формуле V = длина × ширина × высота. Таким образом, объем прямоугольника будет равен 5 см × 3 см × 2 см = 30 см3.
2. Измерение объема жидкости: см3 также используются для измерения объема жидкостей. Например, стандартная емкость для измерения объема жидкости в лаборатории может иметь метки для измерения объема в см3.
3. Расчет объема шара: формула для вычисления объема шара V = 4/3 × π × r3, где r — радиус шара. Если радиус шара равен 2 см, то его объем будет равен 4/3 × 3.14 × (2 см)3 = 33.49 см3.
4. Измерение объема геометрических фигур: см3 используются для измерения объема различных геометрических фигур, таких как параллелепипеды, пирамиды и т.д. Для этого необходимо знать соответствующие размеры фигуры и применить соответствующую формулу для расчета объема.

Это лишь несколько примеров использования см3 в математике. Они позволяют удобно измерять и вычислять объемы различных объектов и жидкостей.

Видео по теме:

Вопрос-ответ:

Что такое см3 в математике?

См3 в математике — это обозначение кубического сантиметра, единицы объема в трехмерном пространстве. Один см3 равен объему куба со стороной в один сантиметр.

Как использовать см3 в математике?

См3 используется для измерения объема тел и веществ. Например, если у вас есть параллелепипед, сантиметры в длину, ширину и высоту, то объем этого тела можно выразить в см3. Также, см3 можно использовать для измерения объема жидкостей, например, в пробирках или емкостях.

Как перевести см3 в другие единицы измерения объема?

Для перевода см3 в другие единицы измерения объема нужно знать соответствующие коэффициенты перевода. Например, 1 см3 равен 0,001 литру, 0,000001 кубическому метру и так далее. Перевод осуществляется умножением или делением на соответствующий коэффициент.

Как считать объем фигуры, если известно значение в см3?

Если известно значение объема фигуры в см3, то для вычисления размеров сторон фигуры нужно знать ее форму. Например, для куба можно найти длину стороны, извлекая кубический корень из значения объема. Для других фигур нужно использовать соответствующие формулы, которые связывают объем с размерами фигуры.

Где можно встретить использование см3 в повседневной жизни?

См3 встречается в повседневной жизни в различных ситуациях. Например, объемы жидкостей в упаковках, емкостях для хранения продуктов или дозаторах препаратов могут быть указаны в см3. Также, размеры предметов, таких как коробки, упаковки или емкости, могут быть указаны в см3.

Каково определение см3 в математике?

См3 (кубический сантиметр) — это единица объема, равная объему куба со стороной в 1 сантиметр. Она широко используется в математике для измерения объема твердых тел, жидкостей и газов.

Как можно использовать см3 в математике?

См3 используется для измерения объема различных объектов и веществ. Например, чтобы найти объем прямоугольного параллелепипеда, необходимо перемножить длину, ширину и высоту в сантиметрах. Полученный результат будет выражен в см3. Также см3 используется для измерения объема жидкостей и газов, например, в химии или физике.

См3 и геометрические фигуры

Для различных геометрических фигур существуют формулы для расчета объема в см3. Например, для прямоугольного параллелепипеда объем вычисляется по формуле: V = a * b * c, где a, b и c – длины сторон параллелепипеда.

Если мы имеем сферу, то ее объем можно вычислить по формуле: V = 4/3 * π * r^3, где r – радиус сферы.

Также в математике существуют и другие геометрические фигуры, для которых можно вычислить объем в см3. Например, для цилиндра формула будет следующей: V = π * r^2 * h, где r – радиус основания цилиндра, а h – высота цилиндра.

Использование см3 в математике позволяет нам измерять и сравнивать объемы различных фигур, что является важным при решении задач и практических ситуаций.

См3 и решение задач

Решая задачи, связанные с см3, необходимо уметь работать с формулой для расчета объема различных геометрических фигур.

Ниже приведены некоторые примеры задач, в которых используется см3:

1. Задача 1: Найдите объем прямоугольного параллелепипеда, если его длина равна 5 см, ширина — 3 см, а высота — 4 см. Для решения этой задачи используется формула: объем = длина x ширина x высота. Подставив значения в формулу, получим: объем = 5 см x 3 см x 4 см = 60 см3.
2. Задача 2: Найдите объем цилиндра, если его радиус основания равен 2 см, а высота — 8 см. Формула для расчета объема цилиндра: объем = площадь основания x высота. Площадь основания цилиндра равна площади круга с радиусом 2 см, то есть 3,14 x (2 см)2. Подставив значения в формулу, получим: объем = 3,14 x (2 см)2 x 8 см = 100,48 см3.
3. Задача 3: Найдите объем конуса, если его радиус основания равен 3 см, а высота — 6 см. Формула для расчета объема конуса: объем = (площадь основания x высота) / 3. Площадь основания конуса равна площади круга с радиусом 3 см, то есть 3,14 x (3 см)2. Подставив значения в формулу, получим: объем = (3,14 x (3 см)2 x 6 см) / 3 = 56,52 см3.

Таким образом, см3 используется для измерения объема различных геометрических фигур и решения связанных с ними задач.