Что такое смешанная дробь в математике

Смешанная дробь — это математическое понятие, которое представляет собой комбинацию целой части и обыкновенной дроби. В этой статье вы узнаете, как представлять и работать со смешанными дробями, а также как преобразовывать их в обыкновенные дроби и обратно.

Смешанная дробь — это числовое выражение, состоящее из целой части и дробной части. Она представляет собой комбинацию целого числа и простой дроби. Смешанная дробь может быть записана в виде целой части, после которой следует дробь. Например, 3 1/2 — это смешанная дробь, где 3 представляет целую часть, а 1/2 — дробную часть.

В математике смешанная дробь используется для представления нецелых чисел, которые могут быть выражены в виде комбинации целого числа и простой дроби. Они могут быть положительными или отрицательными, в зависимости от значения целой части. Например, -2 3/4 — это отрицательная смешанная дробь, где -2 представляет целую часть, а 3/4 — дробную часть.

Смешанные дроби часто используются для упрощения и удобства записи нецелых чисел. Они позволяют представить дробь в более понятной и наглядной форме. Смешанные дроби также могут быть преобразованы в обычную дробь или десятичную дробь для более точных вычислений.

Например, смешанная дробь 2 3/4 можно преобразовать в обычную дробь следующим образом: 2 3/4 = (2 * 4 + 3) / 4 = 11/4. Также смешаная дробь может быть представлена в виде десятичной дроби: 2 3/4 = 2.75.

Смешанные дроби широко применяются в реальной жизни, например, при измерении времени, длины, объема и веса. Они помогают нам представить нецелые значения в более удобном виде и совершать различные математические операции с ними.

Смешанная дробь в математике: определение и примеры

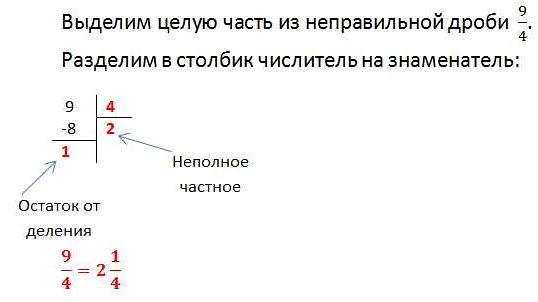
Формально, смешанная дробь записывается в виде a b/c, где a — целая часть числа, b — числитель дробной части, а c — знаменатель дробной части.

Например, число 3 1/4 является смешанной дробью, так как состоит из целой части 3 и дробной части 1/4.

Смешанная дробь может быть представлена в виде обыкновенной дроби путем приведения ее к общему знаменателю. Например, смешанная дробь 3 1/4 может быть записана как обыкновенная дробь 13/4.

Смешанные дроби часто используются для представления времени, длины, объема и других величин, которые могут быть представлены как целая часть и дробная часть.

Примеры:

• 2 3/5 — смешанная дробь, состоящая из целой части 2 и дробной части 3/5.
• 7 2/3 — смешанная дробь, состоящая из целой части 7 и дробной части 2/3.
• 1 1/2 — смешанная дробь, состоящая из целой части 1 и дробной части 1/2.

Видео по теме:

Определение смешанной дроби

Смешаная дробь записывается в виде целого числа, за которым следует дробь вида числитель/знаменатель. Целая часть отделяется от дробной с помощью пробела или знака плюса.

Например, смешаная дробь 3 1/2 представляет собой число, которое содержит целую часть равную 3 и дробную часть равную 1/2.

Смешаные дроби используются для представления нецелых чисел в удобной форме, особенно в контексте повседневной жизни и измерений.

Примеры смешанных дробей

Смешанная дробь представляет собой комбинацию целой части и дробной части. Вот несколько примеров смешанных дробей:

Пример 1:

Смешанная дробь 2 3/4 означает, что у нас есть целая часть (2) и дробная часть (3/4). Это можно преобразовать в обыкновенную дробь, складывая целую часть с дробной: 2 + 3/4 = 8/4 + 3/4 = 11/4.

Пример 2:

Смешанная дробь 3 1/2 означает, что у нас есть целая часть (3) и дробная часть (1/2). Преобразуем ее в обыкновенную дробь: 3 + 1/2 = 6/2 + 1/2 = 7/2.

Пример 3:

Смешанная дробь 4 2/3 означает, что у нас есть целая часть (4) и дробная часть (2/3). Преобразуем ее в обыкновенную дробь: 4 + 2/3 = 12/3 + 2/3 = 14/3.

Таким образом, смешанные дроби представляют собой удобный способ записи чисел, состоящих из целой части и дробной части.

Вопрос-ответ:

Что такое смешанная дробь в математике?

Смешанная дробь — это числовое выражение, состоящее из целой части и обыкновенной дроби. Она имеет вид a + b/c, где a — целая часть, b — числитель обыкновенной дроби, а c — знаменатель обыкновенной дроби.

Как привести смешанную дробь к несократимому виду?

Для приведения смешанной дроби к несократимому виду нужно сначала умножить целую часть на знаменатель обыкновенной дроби, а затем прибавить числитель. Полученная сумма будет новым числителем, а знаменатель остается тот же. Затем можно сократить полученную дробь, если это возможно.

Как складывать и вычитать смешанные дроби?

Для сложения или вычитания смешанных дробей нужно привести их к общему знаменателю. Для этого можно умножить каждую дробь на знаменатель другой дроби. Затем сложить или вычесть числители полученных дробей и оставить общий знаменатель. Если полученная дробь является неправильной, ее можно привести к смешанной дроби.

Можно ли умножать и делить смешанные дроби?

Да, смешанные дроби можно умножать и делить. Для умножения нужно умножить целую часть на множитель, затем умножить числитель на множитель и сложить с произведением целой части и знаменателя. Для деления нужно сначала привести смешанную дробь к обыкновенной дроби, затем обратить вторую дробь и умножить. Результат можно привести к смешанной дроби, если это необходимо.

Смешанная дробь и обыкновенная дробь: разница

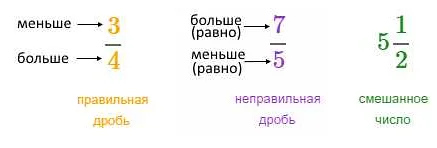
Обыкновенная дробь представляет собой отношение двух целых чисел: числителя и знаменателя. Она записывается в виде дроби, где числитель находится над чертой, а знаменатель — под чертой. Например, дробь 3/4 означает, что числитель равен 3, а знаменатель равен 4.

Смешанная дробь, с другой стороны, состоит из целой части и обыкновенной дроби. Она записывается в виде целого числа, за которым следует дробь. Например, смешанная дробь 2 1/2 означает, что целая часть равна 2, а обыкновенная дробь равна 1/2.

Таким образом, основное отличие между смешанной дробью и обыкновенной дробью заключается в способе записи чисел. Обыкновенная дробь представляет собой отношение двух чисел, а смешанная дробь представляет собой сумму целого числа и обыкновенной дроби.

Обыкновенная дробьСмешанная дробь

3/4

2 1/2

Преобразование смешанной дроби в обыкновенную дробь

Для преобразования смешанной дроби в обыкновенную дробь необходимо выполнить следующие шаги:

1. Умножить целую часть на знаменатель обыкновенной дроби.
2. Прибавить полученное произведение к числителю обыкновенной дроби.
3. Полученная сумма становится новым числителем обыкновенной дроби, а знаменатель остается прежним.

Например, если дана смешанная дробь 3 + (1/4), то:

Шаг 1: 3 * 4 = 12

Шаг 2: 12 + 1 = 13

Итак, смешанная дробь 3 + (1/4) равна обыкновенной дроби 13/4.

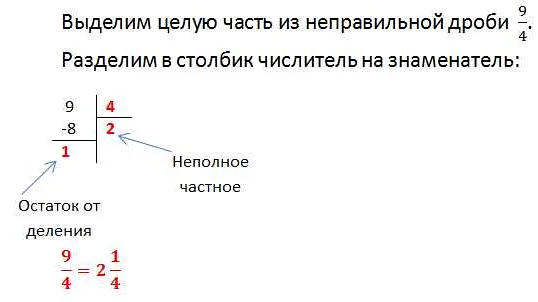
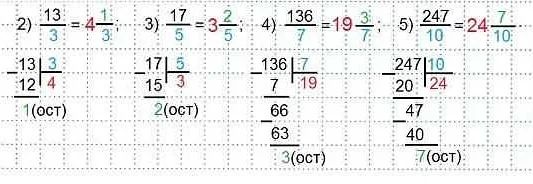
Преобразование обыкновенной дроби в смешанную дробь

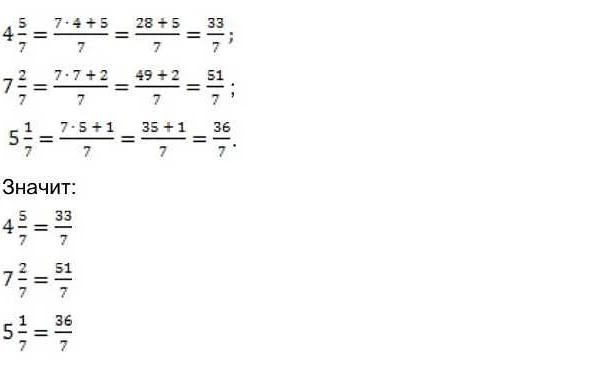
Для преобразования обыкновенной дроби в смешанную дробь необходимо выполнить следующие шаги:

1. Разделить числитель дроби на знаменатель, получив результат в виде неполного частного.
2. Округлить полученное неполное частное до целого числа.
3. Определить остаток от деления числителя на знаменатель.

Полученное целое число станет целой частью смешанной дроби, а остаток от деления станет числителем обыкновенной дроби. Знаменатель остается неизменным.

Например, рассмотрим обыкновенную дробь 7/2. Последовательно выполняя вышеописанные шаги, получим:

• 7 ÷ 2 = 3, неполное частное равно 3.
• Округляем 3 до целого числа, получаем 3.
• Остаток от деления 7 на 2 равен 1.

Таким образом, обыкновенная дробь 7/2 преобразуется в смешанную дробь 3 1/2.

Преобразование обыкновенной дроби в смешанную дробь позволяет более наглядно представить результат и сделать его более понятным для решения математических задач.

Арифметические действия со смешанными дробями

Смешанная дробь состоит из целой части и обыкновенной дроби. При выполнении арифметических действий со смешанными дробями необходимо следовать определенным правилам.

Для сложения и вычитания смешанных дробей нужно сложить или вычесть их целые части отдельно от обыкновенных дробей, а затем сложить или вычесть обыкновенные дроби отдельно. Результатом будет новая смешанная дробь, в которой целая часть и обыкновенная дробь будут соответствовать полученным значениям.

Для умножения смешанных дробей нужно умножить целую часть первой дроби на вторую дробь, затем умножить целую часть второй дроби на первую дробь. Далее нужно умножить обыкновенные дроби и сложить полученные результаты. Итоговый результат будет новой смешанной дробью.

Для деления смешанных дробей нужно представить каждую дробь в виде обыкновенной дроби и выполнить обратную операцию умножения. То есть нужно умножить первую дробь на обратную второй дробь, а затем умножить вторую дробь на обратную первой дробь. Результатом будет новая смешанная дробь.

При выполнении арифметических операций со смешанными дробями важно внимательно следить за правильным представлением дробей и правильным выполнением каждого шага операции.

Применение смешанных дробей в реальной жизни

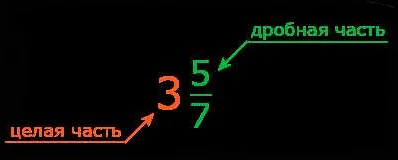
Смешанные дроби широко применяются в реальной жизни для решения различных задач и ситуаций. Они особенно полезны при описании и измерении количества материала или вещества, которое не может быть точно представлено в виде целого числа.

Одним из примеров применения смешанных дробей является измерение времени. Например, если мы хотим выразить время, прошедшее с полудня до вечера, мы можем использовать смешанную дробь. Если полдень соответствует 12 часам, а вечер приходит в 6 часов вечера, то можно сказать, что прошло 6 и 1/2 часа.

Еще одним примером применения смешанных дробей является измерение расстояния. Например, если нам нужно измерить расстояние между двумя городами, мы можем использовать смешанную дробь. Например, если расстояние между городами составляет 120 километров, а мы прошли уже 30 километров, то можно сказать, что мы прошли 1 и 1/4 часть пути.

Смешанные дроби также используются в финансовых расчетах. Например, при расчете процентов или скидок. Если у нас есть сумма денег, которую нужно уплатить, и у нас есть скидка в виде смешанной дроби, то мы можем вычислить сумму с учетом скидки.

Примеры применения смешанных дробей в реальной жизни

Измерение времени

Измерение расстояния

Финансовые расчеты

В заключение, смешанные дроби играют важную роль в реальной жизни и широко используются в повседневных ситуациях. Они позволяют более точно и удобно описывать и измерять различные величины. Понимание смешанных дробей и их применение помогает нам решать задачи и реализовывать практические задачи в различных сферах деятельности.