Что означает понятие «собственная скорость» и как оно применяется в математических задачах?

Собственная скорость — это понятие из области математики, которое используется для описания движения объекта относительно другого объекта или системы координат. В задачах по математике собственная скорость может быть использована для определения скорости и направления движения объекта, а также для расчета времени, необходимого для преодоления определенного расстояния. Узнайте больше о понятии собственной скорости и его применении в математике.

Скорость — одно из ключевых понятий в физике и математике. Но что означает термин «собственная скорость» и как его применяют в задачах по математике? В этой статье мы разберемся с данным понятием и его применением в математических задачах.

Собственная скорость — это скорость объекта относительно некоторой системы отсчета, которая движется вместе с этим объектом. В отличие от абсолютной скорости, которая измеряется относительно стационарной системы отсчета, собственная скорость является относительной скоростью объекта в его собственной системе отсчета.

Применение собственной скорости в задачах по математике позволяет решать различные задачи, связанные с движением объектов. Например, при решении задач на время, расстояние и скорость, необходимо учитывать собственную скорость объекта для получения правильного ответа.

Допустим, у нас есть два объекта, движущиеся друг относительно друга. Один объект движется со скоростью 10 м/с, а второй со скоростью 5 м/с. Что будет, если мы учтем их собственные скорости?

В заключение, собственная скорость является важным понятием в математике и физике, позволяющим более точно описывать движение объектов. Учет этого понятия в задачах по математике помогает получить более точные и корректные результаты.

Важность понимания собственной скорости

Собственная скорость — это скорость, с которой мы решаем математические задачи и выполняем математические операции. Эта скорость может быть измерена в различных единицах, таких как задачи в минуту или операции в секунду. Знание своей собственной скорости позволяет нам определить, как быстро мы работаем и какой уровень эффективности мы достигаем.

Собственная скорость важна не только для оценки личной эффективности, но и для планирования работы и установки реалистичных целей. Зная свою скорость, мы можем определить, сколько времени нам потребуется для выполнения определенного количества задач или операций, и распределить свое время соответственно. Это помогает нам более эффективно использовать свое время и достигать поставленных целей в кратчайшие сроки.

Кроме того, понимание собственной скорости позволяет нам определить области, в которых мы медленнее всего работаем, и сосредоточить свои усилия на их улучшении. Например, если мы замечаем, что мы медленно выполняем умножение чисел двузначной и трехзначной, мы можем уделить больше внимания тренировке этого навыка и развитию навыков быстрого умножения. Это позволит нам повысить свою общую скорость и повысить эффективность при решении задач по математике.

В целом, понимание собственной скорости играет важную роль в достижении успеха в математике. Это помогает нам оценить нашу эффективность, планировать работу и улучшать навыки. Поэтому необходимо уделить время и внимание изучению и пониманию своей собственной скорости и использовать эту информацию для достижения наилучших результатов.

Видео по теме:

Обучение и развитие собственной скорости

Регулярные повторения математических задач позволяют закрепить полученные знания и улучшить навыки решения. Чем больше задач решает ученик, тем быстрее и точнее он становится в решении подобных заданий.

Для эффективного развития собственной скорости необходимо использовать различные методики, которые помогут ученику улучшить свои навыки в решении математических задач. К таким методикам относятся:

• Разделение задач на более простые подзадачи;
• Использование сокращенных записей и символов;
• Работа над улучшением концентрации внимания и быстродействия;
• Использование схематических рисунков и графиков;
• Решение задач в уме.

Помимо этого, важным аспектом развития собственной скорости является уверенность в себе. Ученику необходимо верить в свои возможности и не бояться совершать ошибки. Чем больше практики и опыта он получает, тем больше уверенности в своих действиях у него появляется.

Обучение и развитие собственной скорости требуют времени и терпения. Чтобы достичь хороших результатов, необходимо постоянно тренироваться, повторять материал и применять различные методики. Со временем, ученик заметит, что его собственная скорость в решении задач растет, что поможет ему успешно справляться с математическими заданиями и достигать лучших результатов.

Как измерить собственную скорость

1. Определите, какую задачу вы хотите изучить и измерить свою скорость в ее решении.

2. Составьте план действий для решения задачи. Разбейте задачу на более мелкие шаги и определите порядок их выполнения.

3. Начните решать задачу, следуя заданному плану. Записывайте время, затраченное на каждый шаг решения задачи.

4. После завершения решения задачи, сложите время, затраченное на каждый шаг, чтобы получить общее время решения задачи.

5. Поделите общее время решения задачи на количество шагов, чтобы получить среднее время выполнения каждого шага.

6. Полученное среднее время выполнения каждого шага будет вашей собственной скоростью в решении данной задачи.

Измерение собственной скорости позволяет определить, насколько эффективно вы выполняете математические задачи, и может быть полезным инструментом для улучшения своих навыков и набора знаний в математике.

Составляющие собственной скорости

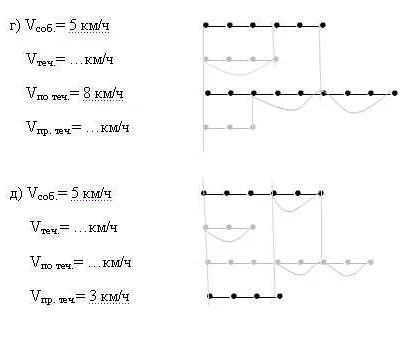
Первая составляющая собственной скорости – это скорость относительно земли. Она определяется относительным движением объекта по отношению к поверхности Земли. Например, если объект движется со скоростью 10 метров в секунду на восток, то его скорость относительно земли будет такой же.

Вторая составляющая – это скорость относительно других объектов. Если объект движется на автомобиле, то его скорость будет относительной к скорости автомобиля. Если автомобиль движется со скоростью 60 километров в час на восток, а объект находится в этом автомобиле и движется со скоростью 10 километров в час на восток, то его скорость относительно автомобиля будет 10 километров в час на восток.

Третья составляющая собственной скорости – это скорость относительно других объектов вращения. Если объект движется на поверхности вращающегося тела, например, на поверхности вращающегося колеса, то его скорость относительно этого колеса будет отличаться от скорости относительно земли или других объектов. Это связано с тем, что объект движется вместе с колесом и имеет дополнительную скорость относительно земли.

Составляющие собственной скорости могут быть сложными и взаимосвязанными. Например, если объект движется на автомобиле, который движется на поверхности вращающегося колеса, то его собственная скорость будет комбинацией всех этих составляющих. Понимание составляющих собственной скорости помогает в решении задач по математике и физике, связанных с движением объектов.

Преимущества высокой собственной скорости

Высокая собственная скорость в задачах по математике обладает рядом преимуществ, которые могут быть полезными как в учебе, так и в повседневной жизни. Вот некоторые из них:

1. Эффективность обучения. Высокая скорость решения задач позволяет быстрее освоить новый материал и продвигаться дальше. Студенты с высокой собственной скоростью могут эффективно использовать время на занятиях и легче усваивать новые концепции и методы решения.

2. Уверенность в своих знаниях. Быстрая и точная работа над задачами позволяет студентам быть уверенными в своих математических способностях. Они могут с легкостью доказывать теоремы, решать сложные уравнения и находить решения к задачам.

3. Повышение конкурентоспособности. В современном мире, где математические навыки являются неотъемлемой частью многих профессий, высокая собственная скорость может стать преимуществом в поиске работы и повышении конкурентоспособности на рынке труда.

4. Улучшение критического мышления. Решение задач по математике требует аналитического мышления, логического рассуждения и способности видеть связи между различными концепциями. Быстрая работа над задачами способствует развитию этих навыков и улучшению критического мышления.

5. Сокращение времени решения задач в повседневной жизни. Математические навыки и высокая собственная скорость решения задач могут быть полезными не только в учебе, но и в повседневной жизни. Они позволяют быстро считать, рассчитывать бюджет, решать практические задачи и принимать обоснованные решения.

В целом, высокая собственная скорость в решении задач по математике является важным навыком, который может принести много пользы как в образовании, так и в реальном мире.

Как повысить собственную скорость

1	Постоянная практика. Чем больше вы решаете задачи, тем более легко и быстро вы будете решать новые задачи.
2	Систематическое обучение. Разбейте материал на небольшие блоки и изучайте их постепенно, поэтапно. Это поможет вам лучше усваивать информацию и легче решать задачи.
3	Использование подходящих методик. Изучите различные методики решения задач и выберите наиболее эффективные для себя. Некоторые методики могут помочь вам решать задачи быстрее и более точно.
4	Анализ ошибок. Разберите свои ошибки и поймите, что именно вы делаете не так. Это поможет вам избегать подобных ошибок в будущем и улучшить свою собственную скорость.
5	Регулярные повторения. Повторяйте ранее изученные материалы и решайте ранее решенные задачи. Это поможет закрепить знания и улучшить собственную скорость.

Помните, что улучшение собственной скорости требует времени и усилий. Постепенно применяйте эти советы и вы обязательно увидите результаты. Удачи вам в совершенствовании математических навыков!

Примеры использования собственной скорости в задачах по математике

Например, рассмотрим задачу о двух автомобилях, движущихся навстречу друг другу. Если скорость одного автомобиля равна v1, а скорость второго автомобиля – v2, то их собственная скорость будет равна сумме скоростей: v = v1 + v2. Используя это понятие, мы можем определить время, за которое автомобили встретятся, зная расстояние между ними.

Другой пример использования собственной скорости – задача о двух поездах, движущихся навстречу друг другу по одной железной дороге. Если скорость первого поезда равна v1, а скорость второго поезда – v2, то их собственная скорость будет равна сумме скоростей: v = v1 + v2. Зная длину железной дороги, мы можем рассчитать время, за которое поезда встретятся.

Также собственная скорость может быть использована для решения задач о движении объектов в одном направлении. Например, если один объект движется со скоростью v1, а другой объект – со скоростью v2, то их относительная скорость будет равна разности скоростей: v = v1 — v2. Это понятие может быть полезно при расчетах времени или расстояния, которые один объект пройдет или преодолеет до встречи с другим объектом.

Таким образом, собственная скорость является важным понятием в задачах по математике и может быть использована для решения различных задач на скорость и движение объектов.

Значение собственной скорости в повседневной жизни

Например, собственная скорость может быть полезной при определении оптимальной скорости движения автомобиля на дороге. Зная собственную скорость автомобиля, водитель может выбрать наиболее безопасную и комфортную скорость, а также оценить время прибытия в пункт назначения.

Собственная скорость также может быть важна при измерении расстояний и времени в путешествиях. Зная собственную скорость поезда или самолета, мы можем оценить время, которое потребуется для достижения места назначения, и спланировать свое время и действия соответствующим образом.

Кроме того, понимание собственной скорости может быть полезным для оценки эффективности работы машин и устройств. Например, зная собственную скорость печати принтера, мы можем определить, сколько времени потребуется для печати большого количества документов и планировать свою работу соответствующим образом.

Примеры использования собственной скорости в жизни

Планирование времени путешествия на автомобиле

Оценка времени прибытия на работу или важное мероприятие

Определение эффективности работы машин и устройств

Оценка времени печати документов на принтере

Таким образом, понимание и использование понятия собственной скорости может быть полезным во многих сферах нашей повседневной жизни, помогая нам принимать осознанные решения и планировать наше время и действия более эффективно.

Вопрос-ответ:

Как определить собственную скорость в задачах по математике?

Собственная скорость в задачах по математике определяется как скорость движения одного объекта относительно другого, измеренная в их общей системе отсчета. Для определения собственной скорости необходимо знать скорость движения объектов относительно наблюдателя и скорость наблюдателя относительно некоторой фиксированной точки.

Зачем нужно знать собственную скорость в задачах по математике?

Знание собственной скорости в задачах по математике позволяет решать различные задачи, связанные с движением объектов. Например, с ее помощью можно вычислить время, за которое объект преодолел заданное расстояние, или определить, насколько изменится скорость объекта после столкновения с другим объектом.

Какие формулы используются для вычисления собственной скорости в задачах по математике?

Для вычисления собственной скорости в задачах по математике используются различные формулы, в зависимости от условий задачи и известных данных. Например, для вычисления собственной скорости объекта, движущегося прямолинейно и равномерно, можно использовать формулу v = s/t, где v — скорость, s — пройденное расстояние, t — время.

Какие факторы могут влиять на собственную скорость в задачах по математике?

Собственная скорость в задачах по математике может зависеть от различных факторов, таких как масса объектов, силы трения, сила гравитации и другие. Например, если на объект действует сила трения, то его собственная скорость будет уменьшаться по мере движения.

Как можно применить понятие собственной скорости в практических задачах по математике?

Понятие собственной скорости можно применить в различных практических задачах по математике, связанных с движением объектов. Например, с ее помощью можно решать задачи о времени и расстоянии, задачи о столкновении объектов, задачи об ускорении и торможении и другие. Знание собственной скорости позволяет более точно описывать и предсказывать движение объектов в реальном мире.