Что такое сумма произведений в математике
Содержимое
- 1 Что такое сумма произведений в математике
- 1.1 Определение суммы произведений
- 1.2 Математическое выражение суммы произведений
- 1.3 Свойства суммы произведений
- 1.4 Примеры использования суммы произведений в математике
- 1.5 Сумма произведений в статистике
- 1.6 Сумма произведений в физике
- 1.7 Вопрос-ответ:
- 1.7.0.1 Что такое сумма произведений в математике?
- 1.7.0.2 Какое применение имеет сумма произведений в математике?
- 1.7.0.3 Как вычислить сумму произведений чисел?
- 1.7.0.4 Какими свойствами обладает сумма произведений в математике?
- 1.7.0.5 Какими примерами применения суммы произведений можно ознакомиться?
- 1.7.0.6 Как определить сумму произведений в математике?
- 1.7.0.7 Какие применения имеет сумма произведений в математике?
- 1.8 Сумма произведений в экономике
- 1.9 Видео по теме:
Сумма произведений является математической операцией, при которой произведения нескольких чисел складываются. Узнайте, как вычислить сумму произведений и применить ее в различных математических задачах.
Сумма произведений – это математическое понятие, которое широко используется в алгебре и арифметике. Оно представляет собой результат сложения нескольких произведений чисел или переменных.
В математике сумма произведений обычно выражается формулой, где слагаемые являются произведениями чисел или переменных. Это позволяет упростить выражения и решать различные задачи.
Примером суммы произведений может служить формула для вычисления суммы арифметической прогрессии. В этом случае каждое слагаемое является произведением номера элемента на разность между первым элементом и общим разностью прогрессии.
Сумма произведений имеет широкое применение в различных областях, включая физику, экономику, статистику и программирование. Она позволяет моделировать и анализировать различные явления и процессы, а также решать задачи оптимизации и определения закономерностей.
В заключение, сумма произведений является важным математическим понятием, которое используется для решения различных задач и моделирования явлений. Её понимание и применение позволяет упростить вычисления и получить более точные результаты.
Определение суммы произведений
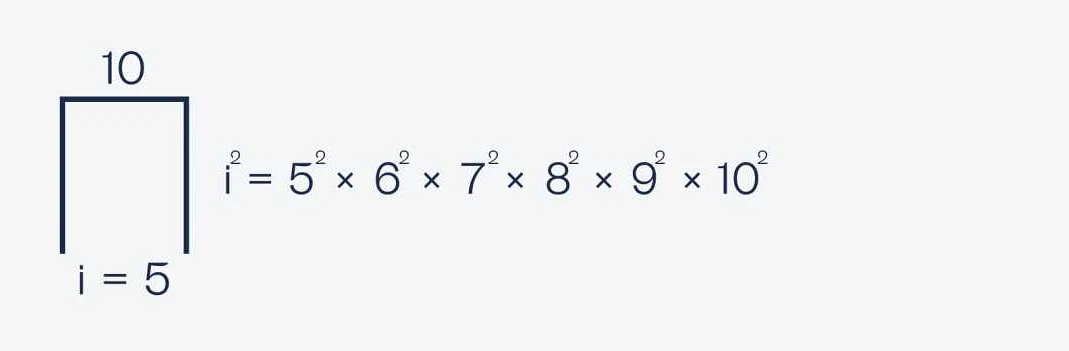
Формально, сумма произведений может быть записана следующим образом:
Сумма произведений: a1b1 + a2b2 + … + anbn
Здесь a1, a2, …, an и b1, b2, …, bn — это числа или переменные, которые участвуют в произведениях. Результатом суммы произведений является число, полученное в результате сложения всех произведений.
Сумма произведений широко используется в алгебре, математическом анализе, теории вероятностей и других областях математики. Она позволяет компактно записывать и вычислять различные математические модели и формулы, а также решать уравнения и системы уравнений.
Математическое выражение суммы произведений

Для записи математического выражения суммы произведений используются специальные символы, такие как символ суммы (∑) и знаки умножения (× или ·). Символ суммы (∑) указывает на то, что нужно выполнить операцию суммирования, а знаки умножения (× или ·) обозначают произведение чисел.
Примером математического выражения суммы произведений может служить следующее выражение:
| ∑ | (a × b) |
В данном примере происходит суммирование произведений двух чисел (a и b). Математически это выражение можно прочитать как «сумма произведений a и b».
Математическое выражение суммы произведений находит свое применение в различных областях математики и физики. Оно используется, например, для вычисления суммы ряда чисел или для нахождения среднего значения набора данных.
Свойства суммы произведений
1. Коммутативность: При сложении нескольких произведений порядок их расположения не важен. То есть, можно менять местами сомножители, и сумма произведений останется неизменной. Например, a*b + c*d = c*d + a*b.
2. Ассоциативность: При сложении трех и более произведений порядок их расположения не важен. То есть, можно менять местами сомножители, и сумма произведений останется неизменной. Например, (a*b) + (c*d) = (c*d) + (a*b).
3. Дистрибутивность: Сумма произведений распространяется на выражение, в котором есть общий множитель. То есть, a*(b + c) = a*b + a*c. Это свойство позволяет упростить выражения и сократить количество операций.
Знание этих свойств суммы произведений позволяет более эффективно работать с вычислениями и упрощать выражения в математических задачах. Они являются основой для дальнейших изучений и применений в алгебре, геометрии и других разделах математики.
Примеры использования суммы произведений в математике
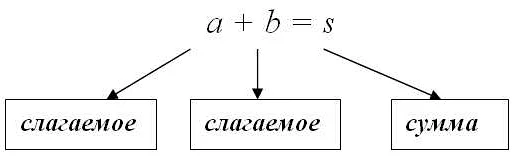
Одним из примеров использования суммы произведений является вычисление скалярного произведения векторов. Скалярное произведение двух векторов равно сумме произведений соответствующих компонент этих векторов. Это позволяет определить, насколько два вектора направлены друг на друга и насколько они подобны друг другу.
Еще одним примером использования суммы произведений является нахождение среднего значения величин. Если даны некоторые величины, то среднее значение можно вычислить как сумму произведений каждой величины на ее вес, деленную на сумму весов. Здесь каждое произведение представляет собой вклад каждой величины в итоговое среднее значение.
Кроме того, сумма произведений может быть использована для вычисления суммы квадратов чисел или для нахождения определенной площади под кривой в математическом анализе. В этих случаях каждое произведение — это квадрат числа или площадь элементарной фигуры, и сумма всех произведений дает итоговый результат.
Таким образом, сумма произведений имеет широкий спектр применений в математике и является важной операцией для решения различных задач и вычислений.
Сумма произведений в статистике
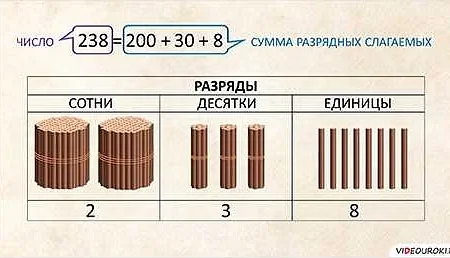
В статистике сумма произведений может быть использована для вычисления коэффициента корреляции между двумя переменными. Коэффициент корреляции показывает степень взаимосвязи между двумя переменными и может быть положительным, отрицательным или нулевым. Чем ближе коэффициент корреляции к единице (положительному или отрицательному), тем сильнее взаимосвязь между переменными.
Для вычисления коэффициента корреляции необходимо найти сумму произведений значений переменных. Для этого каждому значению первой переменной нужно сопоставить соответствующее значение второй переменной, перемножить их и сложить полученные произведения. Затем полученная сумма произведений делится на количество наблюдений.
Первая переменнаяВторая переменнаяПроизведение
| x1 | y1 | x1 * y1 |
| x2 | y2 | x2 * y2 |
| … | … | … |
| xn | yn | xn * yn |
Сумма произведений после деления на количество наблюдений дает коэффициент корреляции.
Сумма произведений также может быть использована для вычисления других статистических показателей, например, ковариации и дисперсии. Она позволяет оценить степень разброса данных и их влияние на результаты исследования.
Сумма произведений в физике
В физике, сумма произведений может использоваться для определения общего вектора силы, когда на объект действует несколько сил. Для этого необходимо умножить каждую силу на соответствующую ей компоненту и сложить полученные произведения. Таким образом можно найти общую силу, действующую на объект.
Также сумма произведений может быть использована для определения общей мощности, когда на систему действует несколько источников энергии. Для этого необходимо умножить каждую мощность на соответствующую ей долю и сложить полученные произведения. Таким образом можно найти общую мощность, производимую системой или получаемую от нее.
Сумма произведений также может использоваться при анализе электрических цепей, где на различные участки цепи действуют различные токи и напряжения. Путем умножения каждого тока на соответствующее ему сопротивление и сложения полученных произведений можно определить общее сопротивление цепи.
Таким образом, сумма произведений является важным инструментом для решения физических задач, где необходимо учесть взаимодействие нескольких факторов или переменных. Она позволяет находить общие характеристики системы, основываясь на взаимодействии ее составляющих частей.
Вопрос-ответ:
Что такое сумма произведений в математике?
Сумма произведений — это арифметическая операция, в которой произведения двух или более чисел складываются. Например, сумма произведений 2*3 и 4*5 равна 6+20=26.
Какое применение имеет сумма произведений в математике?
Сумма произведений широко используется в различных областях математики, физики, экономики и других науках. Например, она применяется в теории вероятностей, в анализе данных, в компьютерной науке и т.д. Сумма произведений позволяет вычислять суммы последовательностей чисел и решать различные задачи.
Как вычислить сумму произведений чисел?
Для вычисления суммы произведений чисел нужно умножить каждое число на другое и затем сложить полученные произведения. Например, если имеется последовательность чисел 2, 3, 4, 5, то сумма произведений 2*3, 3*4, 4*5 будет равна 6+12+20=38.
Какими свойствами обладает сумма произведений в математике?
Сумма произведений обладает рядом свойств, таких как коммутативность (порядок слагаемых можно менять), ассоциативность (слагаемые можно складывать в любом порядке), дистрибутивность (сумму произведений можно раскрыть в сумму сумм). Эти свойства позволяют упрощать вычисления и приводить выражения к более удобному виду.
Какими примерами применения суммы произведений можно ознакомиться?
Примеры применения суммы произведений можно найти в различных областях. Например, в теории вероятностей сумма произведений используется для вычисления вероятности совместного наступления двух событий. В анализе данных сумма произведений используется для построения регрессионных моделей и аппроксимации данных. В экономике сумма произведений применяется при расчете индексов и показателей роста. Это лишь некоторые примеры, которые показывают широту применения суммы произведений.
Как определить сумму произведений в математике?
Сумма произведений в математике определяется как сумма результатов умножения двух или более чисел. Для этого необходимо умножить каждое число друг на друга, а затем сложить полученные произведения.
Какие применения имеет сумма произведений в математике?
Сумма произведений используется в различных областях математики. Например, в алгебре сумма произведений может представлять сумму мономов или полиномов. В анализе сумма произведений может использоваться для приближенного вычисления интегралов. В теории вероятностей сумма произведений может представлять сумму случайных величин. Кроме того, сумма произведений может быть полезной во многих других областях математики и ее применение зависит от конкретной задачи.
Сумма произведений в экономике
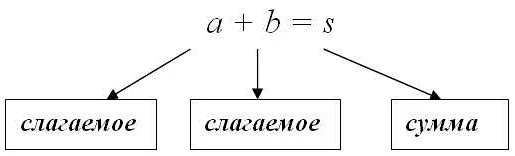
В экономическом анализе сумма произведений позволяет оценить вклад каждого товара или услуги в общую стоимость производства или валового продукта. Это важно для определения структуры экономики и выявления ключевых секторов, которые вносят наибольший вклад в общую экономическую активность.
Сумма произведений также может использоваться для анализа динамики экономического роста и изменения структуры производства. Путем сравнения сумм произведений в разные периоды времени или в разных регионах можно определить, какие секторы экономики растут быстрее или медленнее, и какие товары или услуги приносят большую добавленную стоимость.
В общем смысле, сумма произведений в экономике является инструментом для измерения и анализа экономической активности и ее структуры. Она помогает исследователям, аналитикам и политикам понять, какие секторы экономики являются ключевыми и как они взаимодействуют друг с другом.
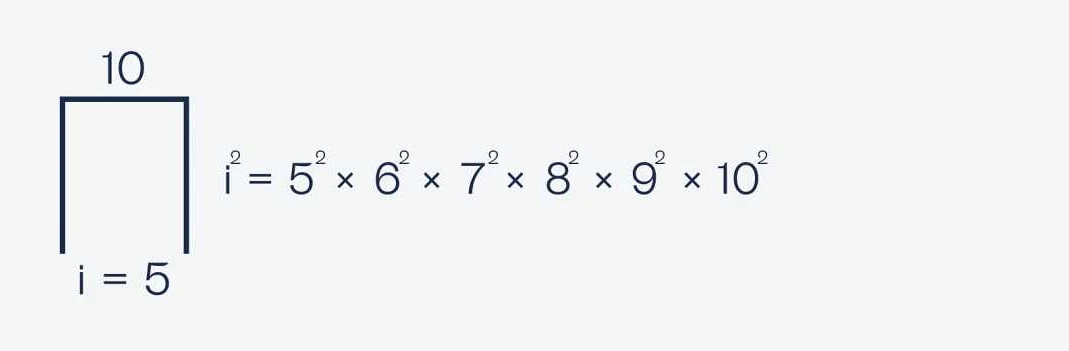


Как интересно узнать, что такое сумма произведений в математике! Это понятие звучит довольно сложно, но на самом деле оно очень полезно и применяется во многих областях. Сумма произведений представляет собой выражение, в котором числа перемножаются и затем складываются. Это может быть очень полезно при решении задач, связанных с расчетами или анализом данных. Например, в экономике можно использовать сумму произведений для вычисления стоимости продуктов или услуг. Также она может быть полезна в физике при расчете силы или энергии. В общем, сумма произведений — это мощный инструмент, который помогает нам понять и анализировать мир вокруг нас. Я очень рада, что узнала об этом понятии!
Очень интересная статья! Я всегда хотела разобраться, что такое сумма произведений в математике. Теперь, благодаря вашей статье, я разобралась. Удивительно, как эта простая математическая операция может иметь так много применений. Я не подозревала, что сумма произведений помогает в решении задач из экономики, физики и даже биологии. Теперь я понимаю, что она является мощным инструментом в анализе данных и моделировании. Уверена, что это знание пригодится мне в повседневной жизни. Спасибо за информативную статью! Жду с нетерпением новых материалов на вашем сайте.