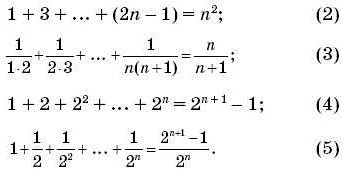Доказательство истинности математического утверждения: методы и примеры

Узнайте о математическом утверждении, которое можно считать правдой только после доказательства его истинности. Подробнее о методах доказательства в математике и примерах применения.

Математические утверждения являются основой математики. Они составляют основу для решения проблем и задач в нашей жизни. Математические утверждения можно опровергнуть или подтвердить через доказательство. Однако, доказательство не всегда означает, что утверждение является истинным.

Доказательство — это процесс установления истинности математического утверждения. В математике существует несколько способов доказательства, которые могут быть использованы в зависимости от типа утверждения. Например, математические индукции, доказательство от противного, математические доказательства и другие способы позволяют установить истинность утверждения или опровергнуть его.

Установление истинности математических утверждений является важным аспектом математики. Оно используется в различных областях, таких как экономика, физика, информатика и других. Важно отметить, что многие математические утверждения были установлены и доказаны многими великими математиками в течение многих лет. А в наши дни мы можем продолжить на этом строить и проверять новые теории и гипотезы, используя современные методы и технологии.

Математика — это игра, где целью является доказательство того, что все, что мы знаем, является правдой.

— Ричард Фейнман

Математические утверждения и их доказательства

Математическое утверждение — это утверждение о математическом объекте или отношении между объектами, которое можно сформулировать точно и четко. Примером такого утверждения может служить теорема Пифагора, которая гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

А доказательство математического утверждения — это процесс, который позволяет показать, что данное утверждение является истинным. Такое доказательство должно быть строгое и логичное, и его результат должен быть убедительным для всех математиков.

Существует несколько основных способов доказательства математических утверждений. Один из них — это дедукция, при которой утверждение выводится из более общего принципа путем логических рассуждений. Еще один способ — это индукция, когда доказательство проводится для конкретного случая, а затем обобщается на все возможные случаи.

В любом случае, доказательство математического утверждения — это важный процесс, который позволяет установить истинность данного утверждения. Благодаря этому процессу математики могут создавать новые теории и находить новые решения для сложных задач.

Видео по теме:

Что такое математическое утверждение?

Математическое утверждение — это утверждение о свойствах математических объектов и операциях, которые на них выполняются. Оно может быть истинным или ложным, но не может быть ни одновременно истинным и ложным. В математике утверждения играют ключевую роль — они являются основным инструментом для формулирования и доказательства теорем.

Математические утверждения могут быть выражены на естественном языке или с помощью формальной математической нотации. Они могут быть простыми или сложными, общими или частными. Примеры математических утверждений: «2 + 2 = 4», «квадрат любого целого числа будет больше, чем это число», «экспонента функции является возрастающей».

Для проверки истинности математических утверждений используются способы доказательства. Существуют различные методы доказательства, но все они должны быть основаны на строгой логической аргументации и следовать правилам математической логики.

Как только утверждение доказано, оно становится теоремой. Теоремы являются основой математики и используются для решения различных проблем в науке и технике. Однако, доказательство теорем может занимать годы, а иногда даже века, что подчеркивает важность математической работы и её вклада в наш мир.

Методы доказательства математических утверждений

Математика – это наука, которая описывает структуру и поведение объектов, используя точные определения и формальные доказательства. 

Доказательство математических утверждений начинается с формулировки предложения, которое будет доказываться. Затем следует выбор подходящего метода доказательства.

Дедуктивный метод доказательства основывается на выведении логических следствий из уже известных утверждений. Он начинается с уже доказанной теории, после чего находится связь между теорией и утверждением, которое доказывается. Если найденная связь логически верна, то утверждение будет также верным.

Индуктивный метод доказательства основывается на обобщении результатов из наблюдений или экспериментов. В математике он используется гораздо реже, чем в других науках. Он заключается в том, что на основании описания некоторого количества примеров можно сделать вывод о том, что это предположение верно вообще и в любом случае.

Противоположное доказательство — это метод, при котором утверждение доказывается путем доказательства его отрицания. Таким образом, утверждение считается доказанным, если его отрицание приводит к противоречию.

Метод математической индукции основывается на доказательстве для каждого натурального числа утверждения, что оно верно. Он начинается с доказательства того, что утверждение истинно для наименьшего натурального числа. Далее доказывается, что если утверждение верно для некоторого числа, то оно также верно и для следующего натурального числа.

Метод от противного заключается в доказательстве того, что если утверждение ложно, то должно произойти что-то противоречивое. Таким образом, путем отрицания утверждения доказывается, что оно истинно.

В зависимости от утверждения и ситуации, выбирается наиболее подходящий метод доказательства.

Доказательства по индукции

Доказательство по индукции это метод математического доказательства, который используется для установления верности утверждений, зависящих от натурального числа. Основная идея заключается в том, что если утверждение верно для некоторого натурального числа, а затем можно показать, что если оно верно для некоторого k, то оно верно и для k+1, то оно будет верно для всех натуральных чисел больших чем изначальное.

Действия при проведении доказательства по индукции можно разделить на две основные части. Первая часть доказательства называется базовый случай, в котором нужно показать, что утверждение верно для некоторого конкретного значения натурального числа. Вторая часть доказательства называется индукционный шаг. В этой части доказательства необходимо показать, что если утверждение верно для некоторого k, то оно верно и для k+1.

При проведении доказательства по индукции очень важно, чтобы базовый случай был правильно определен и истинен, а также чтобы формулировка индукционного шага была четкой и не оставляла места для разных интерпретаций. Индукция является мощным инструментом в математическом анализе и может быть использована для доказательства многих теорем и утверждений.

Важно понимать, что доказательства по индукции не являются универсальным средством доказательства всех теорем. В некоторых случаях можно использовать другие методы доказательства, а иногда доказательство по индукции может быть излишне сложным или неприменимым. Однако, в большинстве случаев доказательство по индукции позволяет уверенно показать верность утверждений, зависящих от натурального числа.

Способы доказательства частных случаев

Доказательство математических утверждений часто представляет собой сложный и многократный процесс, который требует работы над множеством деталей. Однако при доказательстве частных случаев задачи возможно применить более простые способы решения.

Для доказательства частных случаев часто применяется метод индукции – доказательство утверждения для одного случая, а затем обобщение этого случая на все остальные. Этот метод доказательства очень подходит для целочисленных и множественных задач.

Еще одним способом доказательства частных случаев является метод доказательства от противного. Он основывается на том, что если утверждение неверно, то должен существовать контрпример, который покажет, что утверждение неверно. Таким образом, если контрпример не может быть найден, это означает, что утверждение верно.

Также для доказательства соотношений может использоваться метод замены переменных, который заключается в том, чтобы заменить переменные уравнения на более простые или удобные для дальнейшего решения. Этот метод часто используется для решения задач по аналитической геометрии и теории вероятностей.

Важно понимать, что нет универсального способа доказательства, и каждый случай нужно анализировать отдельно, выбирая наиболее подходящий метод в зависимости от условий задачи.

Доказательства от противного

Доказательство от противного – это один из способов доказательства математических утверждений. Он основан на противоположном рассуждении. То есть, предположим, что утверждение неверно, а затем покажем, что это невозможно.

Доказательство от противного может применяться в различных случаях. Например, чтобы доказать, что корень из двух является иррациональным числом, можно предположить, что корень из двух – рациональное число, и затем привести доказательство, противоречащее этому предположению.

Этот способ доказательства особенно полезен, когда утверждение содержит отрицание. Например, для доказательства того, что для любого x, не равного нулю, x умноженное на свое обратное равно 1, можно предположить, что существует такое x, что это утверждение неверно, и затем показать, что это предположение противоречит свойствам умножения.

Однако, нужно помнить, что доказательство от противного не всегда срабатывает. Так, если рассуждение начинается с неверного предположения, то оно может привести к ложным выводам. Поэтому, прежде чем использовать этот способ, важно тщательно продумать рассуждения и предположения.

Доказательства с помощью примеров

Один из способов доказательства математического утверждения — с помощью примеров. Для этого необходимо привести несколько конкретных случаев, которые подтверждают истинность утверждения.

Такой способ доказательства подходит для утверждений, которые имеют небольшое количество возможных вариантов или для которых можно привести примеры с помощью циклических алгоритмов. Например, если необходимо доказать, что все четные числа делятся на 2 без остатка, можно привести примеры: 2, 4, 6, 8, 10 и т.д.

Если же утверждение относится к более общей категории, где количество возможных примеров бесконечно или крайне большое, то такой способ доказательства не будет являться доказательством полной и абсолютной истинности.

Тем не менее, использование примеров может быть полезным для наглядного объяснения и понимания математического утверждения.

• Применение доказательств с помощью примеров имеет следующие преимущества:
  • Простота и наглядность;
  • Помогает проиллюстрировать утверждение на конкретном примере;

Таким образом, доказательства с помощью примеров могут быть эффективным способом доказательства математических утверждений в определенных случаях.

Доказательства с помощью контрпримеров

Доказательство с помощью контрпримера – это метод, который используется для опровержения утверждения путем нахождения примера, который его не подтверждает. Такой пример называется контрпримером.

Пример: утверждение «Все птицы умеют летать» можно опровергнуть, приведя контрпример, например, «пингвин не умеет летать». Этот пример не подтверждает утверждение, следовательно, оно неверно.

Доказательство с помощью контрпримеров может быть полезным в случае, если невозможно найти все возможные примеры, подтверждающие утверждение. В этом случае, достаточно найти один контрпример и опровергнуть утверждение.

Однако, следует быть осторожным при использовании этого метода. Необходимо убедиться, что контрпример действительно противоречит утверждению, а не является исключением исключения. Кроме того, нельзя полагаться только на метод контрпримеров, так как это не гарантирует истинности утверждения во всех случаях.

Доказательства по определению

Доказательство по определению – это способ доказательства, основанный на использовании определения объекта. Если у нас есть определение объекта X, мы можем использовать это определение, чтобы доказать какие-либо утверждения связанные с ним.

Доказательство по определению может быть использовано, когда нам нужно доказать, что объект удовлетворяет определенному свойству, тогда, если мы знаем, что определение этого объекта включает в себя это свойство. Например, чтобы доказать, что треугольник имеет три стороны, можно использовать определение треугольника.

В процессе доказательства по определению мы должны следовать следующим шагам:

1. Представьте определение объекта.
2. Определите, какие свойства включает определение объекта.
3. Докажите, что объект удовлетворяет этим свойствам.

Доказательство по определению может быть очень полезно при доказательстве математических теорем. Он может помочь нам полностью понять определение объекта и использовать его для того, чтобы доказать связанные с ним утверждения.

Доказательства на основе тождеств и эквивалентностей

Одним из наиболее эффективных способов доказательства математических утверждений является использование тождеств и эквивалентностей. Тождества — это равенства, которые справедливы для любых значений переменных, а эквивалентности — это логические выражения, которые имеют одинаковое значение.

В процессе доказательства на основе тождеств и эквивалентностей математик использует различные преобразования и свойства, помогающие ему свести исходное утверждение к более простому виду или к уже доказанной формуле.

Например, чтобы доказать, что выражение (а+b)²=а²+2ab+b², можно воспользоваться тождеством квадрата суммы двух чисел (а+b)²=а²+2ab+b². Таким образом, исходное утверждение преобразуется к уже доказанной формуле, что позволяет сделать вывод об истинности исходного утверждения.

Также часто используется метод эквивалентностей, позволяющий свести сложное выражение к более простому или к уже доказанной формуле. Например, чтобы доказать, что каждое четное число можно представить в виде суммы двух простых чисел (гипотеза Гольдбаха), можно воспользоваться эквивалентностью между простыми числами и бесконечной последовательностью простых чисел, что позволяет сделать вывод об истинности гипотезы.

Доказательства с помощью формальных методов: логические аксиомы и теоремы

Доказательства с помощью формальных методов основываются на логических аксиомах и теоремах. Логические аксиомы – это основные истины, которые не нуждаются в доказательстве и принимаются на веру, а теоремы – это утверждения, которые нужно доказать на основе аксиом.

На основе аксиом формируются логические заключения, которые проверяются на их истинность и достоверность. При этом формальное доказательство – это процесс преобразования исходных формул в новые формулы на основе заранее заданных правил преобразований. После преобразования заключение проверяется на те же самые аксиомы и, если оно истинно, то оно считается доказанным.

Важно отметить, что формальное доказательство может быть полным или неполным. Полное доказательство означает, что все шаги доказательства выполнены корректно и каждый шаг можно отследить. Неполное доказательство может иметь пропущенные шаги или у иметь некоторые необоснованные предположения.

Формальные методы доказательства широко используются в математике и информатике. Например, в математике они применяются для доказательства теорем, в информатике – для проверки правильности протоколов и алгоритмов.

Важно помнить, что формальные методы доказательства не гарантируют истинности утверждения вне зависимости от аксиом. Они говорят о том, что если утверждение истинно относительно заданных аксиом, то оно истинно в целом.

• Формальные методы доказательства основываются на логических аксиомах и теоремах.
• Основные истины, которые не нуждаются в доказательстве и принимаются на веру – логические аксиомы.
• Утверждения, которые нужно доказать на основе аксиом – логические теоремы.
• Преобразование исходных формул в новые формулы на основе заданных правил – процесс формального доказательства.
• Полное формальное доказательство означает выполнение всех корректных шагов.
• Необходимым условием полноты доказательства является возможность отследить каждый шаг.

Установление истинности математических утверждений

Установление истинности математических утверждений — процесс проверки и выявления верности или ложности утверждений в математике. Для этого необходимо прибегать к различным способам доказательства, таким как доказательство от противного, математическая индукция, доказательство по определению и др.

Доказательство от противного — это способ доказательства, в котором предполагается, что утверждение ложно, а затем путем рассуждений и выводов доказывается, что это противоречит уже доказанным утверждениям и принципам математики. Таким образом, изначально ложное утверждение приводится в противоречие с уже доказанными истинными утверждениями.

Математическая индукция — это способ доказательства, применяемый для доказательства истинности для всех натуральных чисел. Этот метод заключается в доказательстве базы индукции (утверждение для минимального натурального числа) и шага индукции (доказательство того, что если утверждение верно для некоторого числа, то оно верно и для следующего числа).

Доказательство по определению — это способ доказательства, в котором используется точное определение понятий и соблюдение аксиом и постулатов математики. Таким образом, для доказательства истинности утверждения необходимо строго следовать его определению и доказать, что все принципы и правила математики соблюдаются.

Важно понимать, что доказательство истинности математического утверждения является основой всей математики и науки в целом. Без строгого доказательства каждого утверждения мы не сможем основывать на это науку и делать новые открытия.

Вопрос-ответ:

Какие методы доказательства могут быть использованы в математике?

В математике используются различные методы доказательства, включая индукцию, от противного, математическую интуицию, доказательство по определению и т.д. Каждый метод имеет свои особенности и может быть использован в зависимости от конкретной задачи и свойств утверждения.

Как установить истинность математического утверждения?

Установление истинности математического утверждения требует строгого доказательства. Для этого необходимо использовать один из методов доказательства, описанных в математической литературе, и провести его до конца, показав, что утверждение верно для всех возможных значений.

Почему математические доказательства часто требуют использования абстрактных концепций?

Математические доказательства требуют использования абстрактных концепций, так как они позволяют обобщить утверждение на большее число случаев и упростить доказательство. Концепции также позволяют строить связи между различными областями математики и расширять область применения утверждения.

Какие проблемы могут возникнуть при доказательстве математического утверждения?

При доказательстве математического утверждения могут возникнуть проблемы с формализацией и ясным определением всех используемых понятий. Также может возникнуть проблема с выбором подходящего метода доказательства, особенно если утверждение требует сложных вычислений или абстрактных концепций.

Как индукция используется для доказательства математических утверждений?

Индукция используется для доказательства утверждений, которые зависят от натурального числа n. Доказательство начинается с базового случая (n = 1) и доказывается, что утверждение верно для n + 1, если оно верно для n. Таким образом, доказательство распространяется на все натуральные числа.

Что такое доказательство от противного?

Доказательство от противного используется, когда требуется доказать, что утверждение не верно. Если предположить, что утверждение верно, и показать, что это противоречит другим утверждениям или правилам, то можно заключить, что исходное утверждение неверно.

Что такое доказательство по определению?

Доказательство по определению используется, когда требуется доказать, что объект или свойство удовлетворяет определению. Для этого необходимо сравнить свойства объекта с определением и показать, что они совпадают.