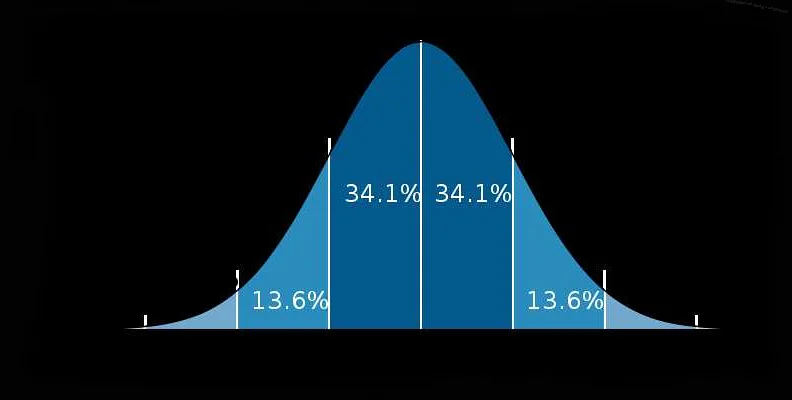
Что такое теория вероятности в математике доступным языком

Узнайте, что такое теория вероятности и как она применяется в математике. В этой статье вы найдете простое объяснение основных концепций и примеры использования теории вероятности в реальной жизни.

Вероятность – это понятие, которое мы используем ежедневно, даже не задумываясь о его математическом основании. Вероятность позволяет оценить, насколько возможно наступление определенного события. Например, когда мы говорим «есть вероятность дождя», мы подразумеваем, что существует шанс, что дождь все-таки пойдет. Именно этим и занимается теория вероятности – она позволяет математически определить и изучить вероятность различных событий.

Основные понятия в теории вероятности – это событие, элементарное событие, пространство элементарных событий и вероятность события. Событие – это некий исход или результат, который может произойти или не произойти. Элементарное событие – это самое простое событие, которое не может быть разделено на более мелкие элементы. Пространство элементарных событий – это множество всех возможных элементарных событий. А вероятность события – это численная характеристика, которая показывает, насколько возможно наступление данного события.

Теория вероятности находит свое применение не только в математике, но и в других науках, таких как статистика, физика, экономика и т.д. Она помогает предсказывать результаты случайных экспериментов, анализировать различные случайные явления и принимать взвешенные решения на основе имеющейся информации. Понимание основных понятий и принципов теории вероятности позволяет лучше ориентироваться в ситуациях, связанных с неопределенностью и рискованными решениями.

Вероятность – это не магия или предсказание будущего, а математический инструмент, который помогает оценить шансы на различные события и принять обоснованные решения.

Определение и принципы

Основными принципами теории вероятности являются:

1. Принцип равномерного распределения вероятностей: Вероятность каждого возможного исхода случайного эксперимента равна. Например, при броске симметричной монеты вероятность выпадения орла и решки равна 0.5.
2. Принцип суммы вероятностей: Сумма вероятностей всех возможных исходов случайного эксперимента равна 1. Например, вероятность выпадения орла или решки при броске монеты равна 1.
3. Принцип независимости: Вероятность совместного наступления двух или более событий равна произведению их вероятностей. Например, вероятность выпадения орла и решки при броске двух монет равна 0.25 (0.5 * 0.5).

Теория вероятности находит применение в различных областях знаний, таких как статистика, физика, экономика, биология и другие. Она помогает в принятии решений в условиях неопределенности и риска, а также позволяет строить математические модели случайных процессов для их изучения и прогнозирования.

История развития

Первые представления о вероятности появились еще в Древнем Египте и Древней Греции, где люди сталкивались с неопределенностью и рискованными ситуациями. Однако, формальное изучение вероятности началось только в XVII веке.

Основоположником теории вероятности считается французский математик Блез Паскаль. В 1654 году он разработал основные принципы теории вероятности, которые были опубликованы в его работе «Трактат о шансах». Паскаль внес значительный вклад в понимание случайных событий и введение математических методов для их анализа.

Позже, другой французский математик Пьер-Симон Лаплас развил теорию вероятности еще дальше. Он сформулировал фундаментальный принцип в теории вероятности — принцип Лапласа, который позволяет определить вероятности событий на основе равномерного распределения. Лаплас также разработал теорему Байеса — одну из основных теорем в статистике.

В XIX веке теория вероятности была активно развиваема и популяризирована другими математиками, такими как Андреи Колмогоров и Ричард фон Мизес. Они установили строгие математические основы теории вероятности и внесли в нее новые понятия и методы.

Сегодня теория вероятности активно применяется в различных областях науки, таких как статистика, физика, экономика, биология и др. Она позволяет анализировать и предсказывать случайные явления, оценивать риски и принимать обоснованные решения на основе вероятностных моделей.

Основные понятия

В теории вероятности существуют несколько основных понятий, которые необходимо понимать для изучения этой области математики:

• Эксперимент: под экспериментом понимается процесс, который может порождать различные исходы. Например, бросок монеты — это эксперимент, который может привести к исходам «орел» или «решка».
• Исход: исход — это конкретный результат эксперимента. В примере с броском монеты исходами будут «орел» или «решка».
• Событие: событие — это некоторое подмножество исходов эксперимента. Например, событием может быть выпадение орла или выпадение решки при броске монеты.
• Вероятность: вероятность — это числовая характеристика события, отражающая степень его возможности. Вероятность события может быть выражена числом от 0 до 1, где 0 означает полную невозможность события, а 1 — его полную достоверность.
• Случайная величина: случайная величина — это величина, которая принимает различные значения в зависимости от исхода эксперимента. Например, случайной величиной может быть число выпавших орлов при серии бросков монеты.
• Функция вероятности: функция вероятности — это функция, которая сопоставляет каждому значению случайной величины вероятность его возникновения. Например, функция вероятности может определить вероятность выпадения определенного количества орлов при броске монеты.

Понимание этих основных понятий позволит более глубоко изучить и понять теорию вероятности в математике.

Математическая модель

Теория вероятности использует математическую модель для изучения случайных явлений. Математическая модель представляет собой абстрактное представление реального мира, которое позволяет упростить и анализировать сложные ситуации.

В рамках теории вероятности математическая модель может быть представлена в виде набора вероятностных событий, множества их исходов и правил для вычисления вероятностей.

Математическая модель позволяет исследовать различные случайные явления, такие как броски монеты, выборки из набора данных или события в природе, и предсказывать их результаты с помощью вероятностных расчетов.

Использование математической модели в теории вероятности позволяет не только лучше понять случайные явления, но и применять эти знания в различных областях, таких как физика, экономика, статистика и многих других.

Примеры применения

Теория вероятности находит широкое применение в различных областях, включая:

1. Статистика: теория вероятности используется для анализа данных, оценки вероятности различных событий и построения статистических моделей.
2. Финансы: теория вероятности позволяет оценить риски и вероятность получения прибыли при инвестировании, а также прогнозировать изменения на финансовых рынках.
3. Инженерия: теория вероятности применяется при проектировании и анализе сложных систем, таких как телекоммуникационные сети, электрические сети и транспортные системы.
4. Медицина: теория вероятности используется для оценки вероятности заболевания, эффективности лекарственных препаратов и прогнозирования результатов медицинских исследований.
5. Искусственный интеллект: теория вероятности является основой для многих алгоритмов машинного обучения и искусственного интеллекта, позволяя моделировать и предсказывать поведение систем и процессов.

Это лишь некоторые примеры применения теории вероятности. Ее основные принципы и методы находят применение во множестве других областей и наук, помогая анализировать и понимать вероятностные явления и события.

Типы вероятностей

Теория вероятности включает в себя различные типы вероятностей, которые используются для описания различных случайных событий. Вот некоторые из них:

1. Априорная вероятность: это вероятность события, которую можно определить до проведения эксперимента или наблюдения. Она основывается на знаниях и предположениях о возможных исходах события.

2. Апостериорная вероятность: это вероятность, которую можно определить после проведения эксперимента или наблюдения. Она основывается на полученных данных и обновляется с учетом новой информации.

3. Условная вероятность: это вероятность наступления одного события при условии, что уже произошло другое событие. Она используется для моделирования зависимостей между различными событиями.

4. Совместная вероятность: это вероятность наступления двух или более событий одновременно. Она используется для моделирования ситуаций, в которых несколько событий происходят параллельно или в определенном порядке.

5. Независимая вероятность: это вероятность наступления одного события, которое не зависит от наступления других событий. Вероятность наступления каждого события не влияет на вероятность наступления других событий.

Эти типы вероятностей помогают ученым и математикам описывать и анализировать различные случайные события, которые могут возникнуть в реальном мире.

Теорема Байеса

Формально, теорема Байеса утверждает, что для двух событий A и B, вероятность события A при условии, что событие B произошло, равна произведению вероятности события B при условии, что событие A произошло, на вероятность события A и делению на вероятность события B:

P(A|B) = (P(B|A) * P(A)) / P(B)

Суть теоремы Байеса заключается в том, что она позволяет обновлять вероятности на основе новой информации. Например, если у нас есть некоторая гипотеза A, и мы получаем наблюдение B, то теорема Байеса позволяет нам пересчитать вероятность гипотезы A, учитывая это наблюдение.

Теорема Байеса находит свое применение в различных областях, включая машинное обучение, статистику, биологию и искусственный интеллект. Она является мощным инструментом для анализа данных и принятия решений на основе вероятностных моделей.

Вопрос-ответ:

Что такое теория вероятности?

Теория вероятности — это раздел математики, который изучает случайные явления и вероятности их возникновения. Она используется для оценки вероятности различных исходов и принятия решений на основе этих вероятностей.

Зачем нужна теория вероятности?

Теория вероятности нужна для анализа и предсказания случайных явлений в различных областях, таких как статистика, физика, экономика и другие. С ее помощью можно оценить вероятность различных исходов, а также принять решение на основе этих вероятностей.

Какие понятия связаны с теорией вероятности?

В теории вероятности используются такие понятия, как вероятность, случайная величина, событие, вероятностное пространство, математическое ожидание, дисперсия и другие. Эти понятия помогают описывать и анализировать случайные явления и их вероятности.

Как определить вероятность?

Вероятность — это числовая характеристика случайного события, которая указывает, насколько оно вероятно возникнуть. Вероятность может быть определена как отношение числа благоприятных исходов к общему числу возможных исходов. Например, для броска правильной монеты вероятность выпадения орла или решки равна 1/2.

Как применяется теория вероятности в реальной жизни?

Теория вероятности применяется во многих областях реальной жизни. Например, она используется для расчета вероятности победы команды в спортивном матче, для оценки рисков в финансовых инвестициях, для анализа данных в научных исследованиях, для прогнозирования погоды и многих других задач. Она помогает принимать обоснованные решения на основе вероятностной оценки и предсказания возможных исходов.

Видео по теме: