Что такое тета в математике

Тета (θ) в математике обозначает угол в геометрии или переменную в уравнении. Узнайте, как использовать тета в различных математических контекстах и какие свойства угла тета имеют в геометрии.

В математике тета — одна из наиболее важных греческих букв, которая широко используется в различных областях науки. Тета обычно обозначается символом θ и является одной из 24 букв греческого алфавита.

Понятие тета имеет различные значения в разных математических дисциплинах. В тригонометрии, тета может обозначать угол. Вероятностной теории, тета может относиться к параметру распределения. В физике, тета может представлять собой угол поворота или положение объекта в пространстве.

Применение тета в математике широко распространено. Она играет важную роль в теории вероятности и статистике, тригонометрии, геометрии, физике и других научных дисциплинах. Знание и понимание тета позволяют решать различные задачи, моделировать и предсказывать различные явления и являются ключевыми в понимании многих математических концепций и принципов.

Знание и использование тета в математике являются важными для развития науки и практического применения математических методов в различных областях. Она позволяет ученым и исследователям анализировать данные, моделировать реальные явления, предсказывать результаты экспериментов и разрабатывать новые математические методы и теории.

В данной статье мы рассмотрим различные аспекты понятия тета в математике, его применение и важность для научных исследований. Мы рассмотрим основные определения и свойства тета, а также примеры его использования в различных областях математики и науки в целом. Также мы рассмотрим некоторые интересные факты о тета и его историческом значении.

Определение теты в математике

Тета может быть измерена в радианах или градусах. В радианах, полный оборот (360 градусов) равен 2π радианам, поэтому тета может быть выражена как число между 0 и 2π. В градусах, полный оборот равен 360 градусам, поэтому тета может быть выражена как число между 0 и 360.

Тета часто используется в геометрии для определения положения точек на плоскости или в пространстве. Например, в полярных координатах, тета определяет угол между положительным направлением оси X и линией, соединяющей начало координат с точкой.

Тета также используется в тригонометрии, где она является одним из параметров для определения значений тригонометрических функций, таких как синус, косинус и тангенс.

Тета имеет широкое применение в различных областях математики и физики, включая геометрию, тригонометрию, физику волн и другие. Понимание понятия теты в математике является важным для решения задач и работы с углами в различных контекстах.

Значение теты в геометрии

В геометрии тета (θ) обычно обозначает угол, который измеряется в радианах или градусах. Угол тета может быть определен как отношение длины дуги окружности к радиусу.

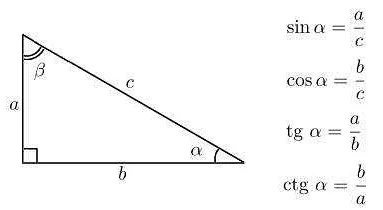
Тета используется в различных геометрических конструкциях и формулах. Например, в треугольниках угол тета может быть одним из углов треугольника или углом между сторонами. Он также может быть использован для измерения поворота или направления объекта в пространстве.

Кроме того, тета может быть использована для определения тригонометрических функций, таких как синус (sin(θ)), косинус (cos(θ)) и тангенс (tan(θ)). Эти функции широко используются в геометрии и физике для решения различных задач, связанных с углами и сторонами фигур.

Значение тета в геометрии имеет важное значение и используется для изучения и анализа различных геометрических форм и конструкций.

Тета в тригонометрии: основные свойства

Основные свойства тета в тригонометрии:

• Периодичность: Значение тригонометрических функций периодически повторяется через равные промежутки углов.
• Зависимость: Значения тригонометрических функций зависят от значения угла тета.
• Соотношения: Между тригонометрическими функциями существуют определенные соотношения, такие как тождество Пифагора и формулы связи различных функций между собой.
• Геометрическое представление: Тригонометрические функции могут быть представлены геометрически с помощью остроугольного треугольника или единичной окружности.
• Применение: Тета и тригонометрические функции широко используются в математических и физических расчетах, например, при моделировании колебательных систем, изучении периодических явлений и решении геометрических задач.

Изучение свойств тета и его взаимосвязи с тригонометрическими функциями помогает понять природу углов и их влияние на различные математические и физические явления.

Функция теты и ее график

График функции теты представляет собой кривую, которая начинается в начале координат (0,0) и идет вдоль положительной полуоси x. При этом значение функции равно углу, измеряемому в радианах, который соответствует длине дуги окружности, проходящей через точку (x,0) и начало координат.

График функции теты имеет период 2π и является периодическим, что означает, что он повторяется через каждые 2π радиан. Также известно, что функция теты является нечетной функцией, что означает, что график симметричен относительно начала координат.

На графике функции теты можно наблюдать следующие характеристики:

• В точке (0,0) функция равна 0 радиан (угол, измеряемый в радианах).
• При x > 0 функция возрастает монотонно от 0 до π радиан (угол, измеряемый в радианах).
• При x < 0 функция убывает монотонно от 0 до -π радиан (угол, измеряемый в радианах).

График функции теты имеет множество применений в различных областях науки и техники, таких как физика, инженерия, компьютерная графика и другие. Он используется для моделирования и решения различных задач, связанных с углами и вращением.

Тета в алгебре: роль в уравнениях и системах

Тета может быть использована, например, при решении уравнений с тригонометрическими функциями. В таких уравнениях требуется найти значения углов, удовлетворяющие определенным условиям. Тета часто используется для обозначения таких углов.

Также тета может быть введена при решении систем уравнений, где каждое уравнение имеет несколько неизвестных. В этом контексте тета обозначает значение одной из неизвестных переменных.

Для удобства использования тета в алгебре можно представить в виде таблицы, где в первом столбце указывается уравнение или система уравнений, а во втором столбце — значение тета:

Уравнение/Система уравненийЗначение тета

sin(θ) = 0.5	θ = π/6
cos(θ) + sin(θ) = 1	θ = 0
2x + 3y = 6	θ = x

Таким образом, тета играет важную роль в алгебре при решении уравнений и систем уравнений, обозначая неизвестные углы или переменные.

Тета в статистике и вероятности

В статистике и вероятности тета (θ) обозначает параметр, который используется для описания вероятностного распределения или статистической модели.

В контексте вероятности, тета может обозначать параметр вероятностного распределения, такого как среднее значение (математическое ожидание) или дисперсия.

Например, в распределении Бернулли (двоичном распределении) тета обозначает вероятность успеха в одном испытании. В распределении Пуассона тета обозначает среднее число событий, которые происходят за фиксированный промежуток времени или в пространстве.

В статистике, тета может обозначать параметр модели, который определяет форму и характеристики данных. Например, в линейной регрессии тета обозначает коэффициент наклона, который показывает, как одна переменная зависит от другой.

Тета является важным понятием в статистике и вероятности, поскольку позволяет описывать и анализировать различные явления и моделировать их с помощью математических методов.

Тета в математической физике: применение в уравнениях

В уравнениях математической физики, тета может использоваться для описания колебаний, вращательных движений и других физических процессов, где угол или периодическая функция играют важную роль. Например, в уравнении колебаний математического маятника, тета может представлять угол отклонения маятника от равновесного положения.

Тета также может быть использована для описания волновых процессов. Например, в уравнении волнового уравнения, тета может представлять фазу волны или угол распространения. Такое использование теты позволяет описывать волновые процессы, такие как звуковые и световые волны, электромагнитные волны и многое другое.

Таким образом, тета играет важную роль в математической физике, позволяя ученым описывать и решать сложные физические проблемы. Ее применение в уравнениях позволяет получать точные и понятные результаты, которые могут быть использованы для прогнозирования и анализа физических явлений.

Видео по теме:

Зачем нужны тета-функции в математике?

Тета-функции в математике имеют широкий спектр применений. В частности, они используются при решении задач в теории чисел, комбинаторике, анализе и математической физике. Они позволяют вычислить различные суммы, произведения и интегралы, а также решить некоторые дифференциальные и интегральные уравнения. Тета-функции также играют важную роль в теории модулярных форм и модулярных функций.

Какие результаты можно получить с помощью тета-функций?

С помощью тета-функций можно получить различные результаты и формулы. Например, с их помощью можно вычислить суммы квадратов и кубов натуральных чисел, количество способов разложить число на слагаемые, количество целочисленных решений некоторых диофантовых уравнений и другие комбинаторные задачи. Тета-функции также позволяют получить асимптотические формулы для различных функций и рядов, а также исследовать модулярные формы и функции.