Что называют тангенсом угла в математике

Тангенс угла – это тригонометрическая функция, определенная как отношение противоположной стороны треугольника к прилежащей стороне. Узнайте, как определить тангенс угла и как он применяется в математике.

Тангенс угла — одна из основных тригонометрических функций, которая широко применяется в математике и других науках. Определение тангенса угла основывается на соотношении между противоположным и прилежащим катетами в прямоугольном треугольнике. Таким образом, тангенс угла можно выразить как отношение длины противоположного катета к длине прилежащего катета.

Тангенс угла имеет несколько свойств, которые позволяют использовать его в различных математических задачах. Во-первых, тангенс угла является периодической функцией с периодом π, что означает, что значения тангенса повторяются при изменении угла на π или его кратные. Во-вторых, тангенс угла может принимать любые значения от минус бесконечности до плюс бесконечности, включая ноль.

Тангенс угла также широко используется в различных областях науки и техники. Например, в физике он применяется при решении задач, связанных с движением и силами, а в геометрии — для нахождения углов и расстояний. Благодаря своим свойствам и удобным математическим выражениям, тангенс угла является одним из важных инструментов, который помогает ученым и инженерам в исследовании и решении сложных задач.

Определение тангенса угла

Математический символ тангенса угла выглядит как отношение sin и cos: tg(x) = sin(x) / cos(x), где x — значение угла.

Значение тангенса угла может быть отрицательным, положительным или нулевым, в зависимости от расположения угла на координатной плоскости. Если тангенс угла положительный, то угол находится в первом или третьем квадранте. Если тангенс угла отрицательный, то угол находится во втором или четвертом квадранте.

Тангенс угла имеет также периодическую функцию, с периодом pi или 180 градусов. Это означает, что значения тангенса повторяются каждые 180 градусов или pi радиан.

Тангенс угла широко применяется в различных областях науки и техники, включая физику, инженерию, навигацию, строительство и другие. Он используется для решения задач, связанных с треугольниками, углами и прямыми линиями.

Тангенс угла — основное понятие

Тангенс угла определяется как отношение противоположной стороны к прилежащей стороне треугольника. Обозначается символом «tg». Для любого данного угла, тангенс можно выразить как отношение синуса угла к косинусу угла:

tg(α) = sin(α) / cos(α)

Тангенс угла является безразмерной величиной, значит он не имеет единицы измерения. Значение тангенса всегда может быть представлено числом, как положительным, так и отрицательным.

Тангенс угла имеет множество свойств и применений в математике и других науках. Он используется в тригонометрии, геометрии, физике и инженерных расчетах. Также тангенс угла является важным понятием при решении задач, связанных с определением высоты, длины и расстояния.

Тангенс угла — геометрическая интерпретация

Геометрический смысл тангенса заключается в том, что он показывает, насколько круто угол α наклонен к оси абсцисс. Если tg(α) > 0, то угол наклонен вправо от оси абсцисс. Если tg(α) < 0, то угол наклонен влево от оси абсцисс. А если tg(α) = 0, то угол α параллелен оси абсцисс.

Для вычисления тангенса угла α можно использовать таблицу значений тангенса или специальный калькулятор. Также можно использовать формулу tg(α) = sin(α) / cos(α), где sin(α) — синус угла α, а cos(α) — косинус угла α.

Тангенс угла имеет множество практических применений. Он широко используется в тригонометрии для решения задач на построение треугольников, вычисление расстояния и высоты, а также для моделирования в физике и инженерии.

Угол αТангенс угла tg(α)

0°	0
30°	0.577
45°	1
60°	1.732
90°	∞

Тангенс угла — математическое определение

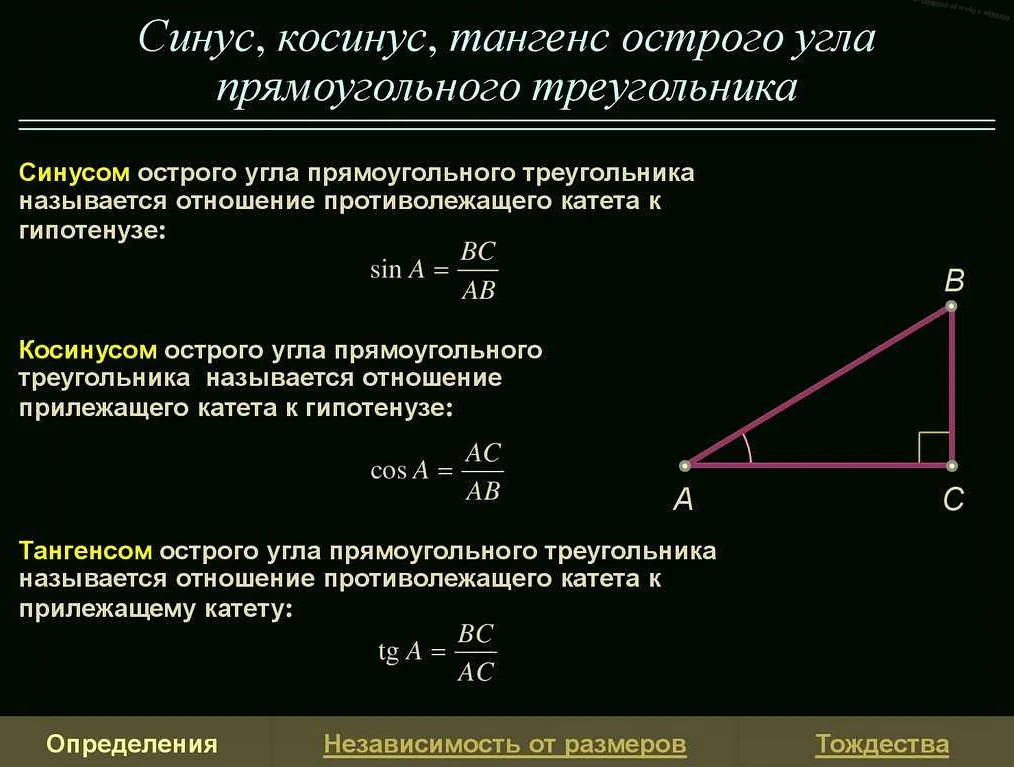
Математический вид тангенса угла можно представить следующим образом:

tg(α) = sin(α) / cos(α)

где sin(α) — синус угла α, а cos(α) — косинус угла α.

Тангенс угла определен только для углов, которые не являются кратными 180 градусам, так как в этих случаях знаменатель tan(α) будет равен нулю, что приведет к делению на ноль.

Зная тангенс угла, можно вычислить значение самого угла. Для этого используют обратную функцию тангенса, обозначаемую как arctg или atan. Например, если tg(α) = 0,5, то α = arctg(0,5) ≈ 26,57°.

Тангенс угла широко используется в различных областях математики, физики, инженерии и других науках. Он применяется при решении задач, связанных со смещением, скоростью, гармоническими колебаниями, а также при вычислении углового ускорения, градиента и т. д.

Свойства тангенса угла

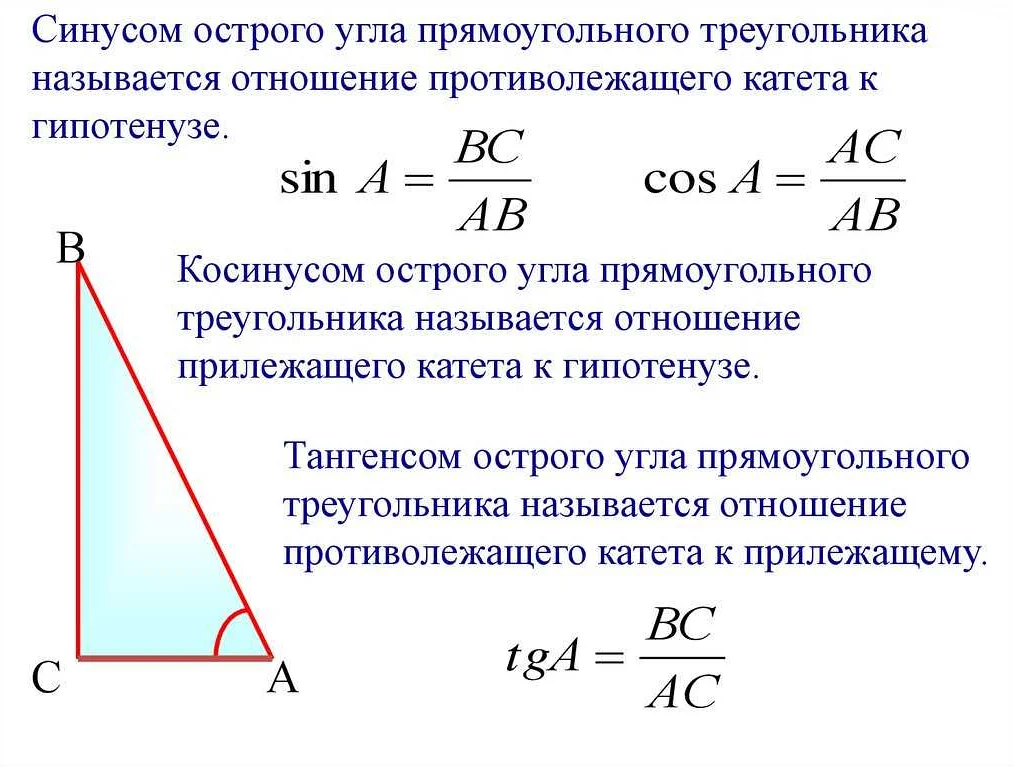
• Тангенс угла является бесконечно дифференцируемой функцией на своей области определения.
• Значение тангенса угла может быть положительным, отрицательным или нулевым, в зависимости от значения угла.
• Тангенс угла равен нулю при угле, равном нулю или кратном π.
• Тангенс угла является периодической функцией с периодом π. Это значит, что значение тангенса повторяется через каждые π радиан или 180 градусов.
• Тангенс является неограниченной функцией, что означает, что его значение может приближаться к бесконечности при некоторых значениях угла.
• Тангенс угла является четной функцией, что означает, что для любого угла θ, тангенс (-θ) = -тангенс (θ).

Эти свойства тангенса угла могут быть использованы для решения различных математических задач и в приложениях, где требуется анализ углов и их отношений.

Свойство периодичности тангенса угла

Одним из важных свойств тангенса угла является его периодичность. То есть, значение тангенса угла повторяется через определенные интервалы.

Тангенс угла имеет период равный π (пи). Это означает, что значение тангенса угла повторяется через каждые π радиан или 180 градусов.

Например, если тангенс угла равен 1 на интервале от 0 до π (пи), то он будет равен -1 на интервале от π до 2π (два пи), и так далее.

Это свойство периодичности тангенса угла позволяет нам анализировать и вычислять его значения в различных углах, используя значения тангенса на одном периоде.

Свойство симметрии тангенса угла

Симметрия тангенса угла заключается в следующем: если значение тангенса угла равно определенному числу, то значение тангенса этого угла, но с противоположным знаком, будет равно тому же числу. Иными словами, тангенс угла и его отрицательный тангенс равны по модулю.

Формально, свойство симметрии тангенса угла можно записать следующим образом:

• Если tg(α) = a, то tg(-α) = -a.

Это свойство позволяет упростить вычисления и решение задач, связанных с тригонометрией. Например, если нужно найти значение тангенса угла, но известно только значение его отрицательного тангенса, то можно использовать свойство симметрии и просто сменить знак результата.

Симметрия тангенса угла также имеет важное практическое применение в различных областях, таких как физика, инженерия и компьютерная графика, где тригонометрия широко используется для моделирования и расчетов.

Свойство монотонности тангенса угла

Из определения тангенса угла следует, что тангенс увеличивается при увеличении значения синуса угла и уменьшении значения косинуса угла. Таким образом, при увеличении значения угла, его синус увеличивается, а косинус уменьшается. Следовательно, значение тангенса растет. Аналогично, при уменьшении значения угла, его синус уменьшается, а косинус увеличивается, что влечет уменьшение значения тангенса.

Монотонность тангенса угла имеет важное практическое применение в различных областях, включая геометрию, физику, инженерию и другие науки. Знание свойства монотонности тангенса позволяет анализировать и решать задачи, связанные с изменением значений углов и соответствующих им тангенсов.

Видео по теме:

Вопрос-ответ:

Что такое тангенс угла?

Тангенс угла — это отношение противоположной стороны треугольника к прилежащей стороне. Математически, тангенс угла равен синусу угла, деленному на косинус угла.

Как определить значение тангенса угла?

Значение тангенса угла можно определить с помощью таблиц или калькулятора. Для этого нужно разделить значение синуса угла на значение косинуса угла.

Какие свойства имеет тангенс угла?

Основными свойствами тангенса угла являются: периодичность, нечетность и ограниченность. Тангенс угла периодичен с периодом π, то есть его значения повторяются через каждые π радиан или 180 градусов. Тангенс угла также является нечетной функцией, то есть tan(-θ) = -tan(θ). Ограниченность тангенса угла означает, что его значения лежат в интервале от -∞ до +∞.

Как можно применить тангенс угла в математике?

Тангенс угла широко применяется в различных областях математики. Например, в геометрии тангенс угла используется для определения высоты треугольника, а также для вычисления площади треугольника. В тригонометрии тангенс угла используется для решения задач на нахождение длины стороны треугольника или нахождение неизвестного угла.

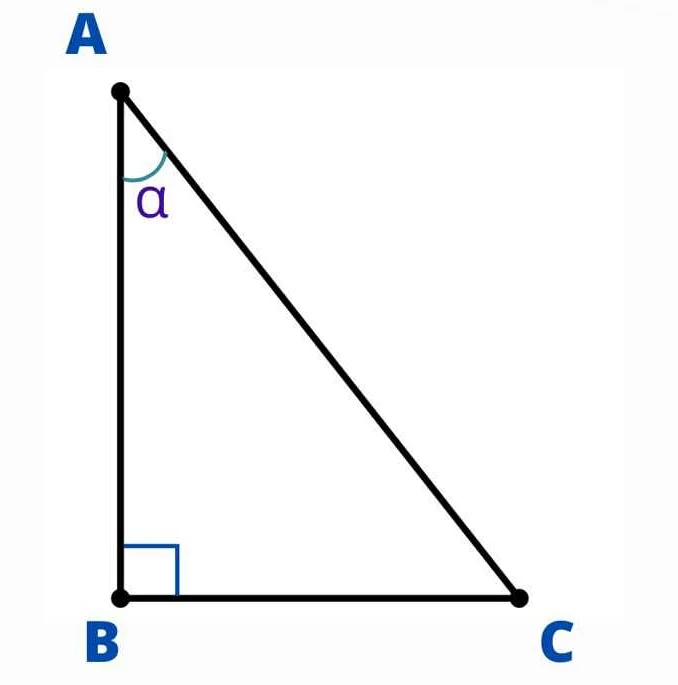
Как найти значение тангенса угла в прямоугольном треугольнике?

Для нахождения значения тангенса угла в прямоугольном треугольнике необходимо разделить длину противоположной стороны на длину прилежащей стороны треугольника. Например, если противоположная сторона равна 4, а прилежащая сторона равна 3, то тангенс угла будет равен 4/3.

Что такое тангенс угла?

Тангенс угла — это одно из тригонометрических отношений, которое определяется как отношение противоположной стороны к прилежащей стороне прямоугольного треугольника

Применение тангенса угла

Сфера примененияОписание

Геометрия	Тангенс угла используется для нахождения значений углов в треугольниках, а также для решения задач на построение и измерение углов.
Физика	В физике тангенс угла используется для расчетов векторных величин, например, для определения направления и силы вектора.
Инженерия	В инженерии тангенс угла используется при проектировании и расчете конструкций, например, для определения угла наклона крыши или опоры.
Астрономия	В астрономии тангенс угла используется для определения высоты звезды или планеты, а также для определения времени восхождения и захода.
Экономика	В экономике тангенс угла используется для анализа и прогнозирования данных, например, при расчете коэффициента роста или изменения цен.

Таким образом, применение тангенса угла является важным инструментом для решения различных задач и проведения исследований в различных областях знаний.

Применение тангенса угла в тригонометрии

Одним из главных применений тангенса угла является решение задач геометрии и тригонометрии. Тангенс позволяет находить значения углов и длин сторон треугольников, основываясь на известных значениях других сторон и углов. Это позволяет решать задачи на построение треугольников, нахождение неизвестных углов и длин сторон.

Тангенс также широко используется в различных областях науки и инженерии. Например, в физике он помогает рассчитывать траектории движения тел, определять углы наклона поверхностей и другие параметры. В электротехнике тангенс используется для расчета фазовых сдвигов и импедансов в электрических цепях.

Также тангенс угла используется в астрономии для определения положения небесных объектов. Он помогает измерять углы наклона и наблюдать движение планет и звезд.

Тангенс угла имеет много других применений в математике и ее приложениях. Он используется в тригонометрических рядах, дифференциальных и интегральных уравнениях, математической статистике и других областях. Поэтому понимание тангенса угла и его свойств является важным для изучения математики и ее применения в различных научных и технических областях.