Что обозначает в математике угол альфа

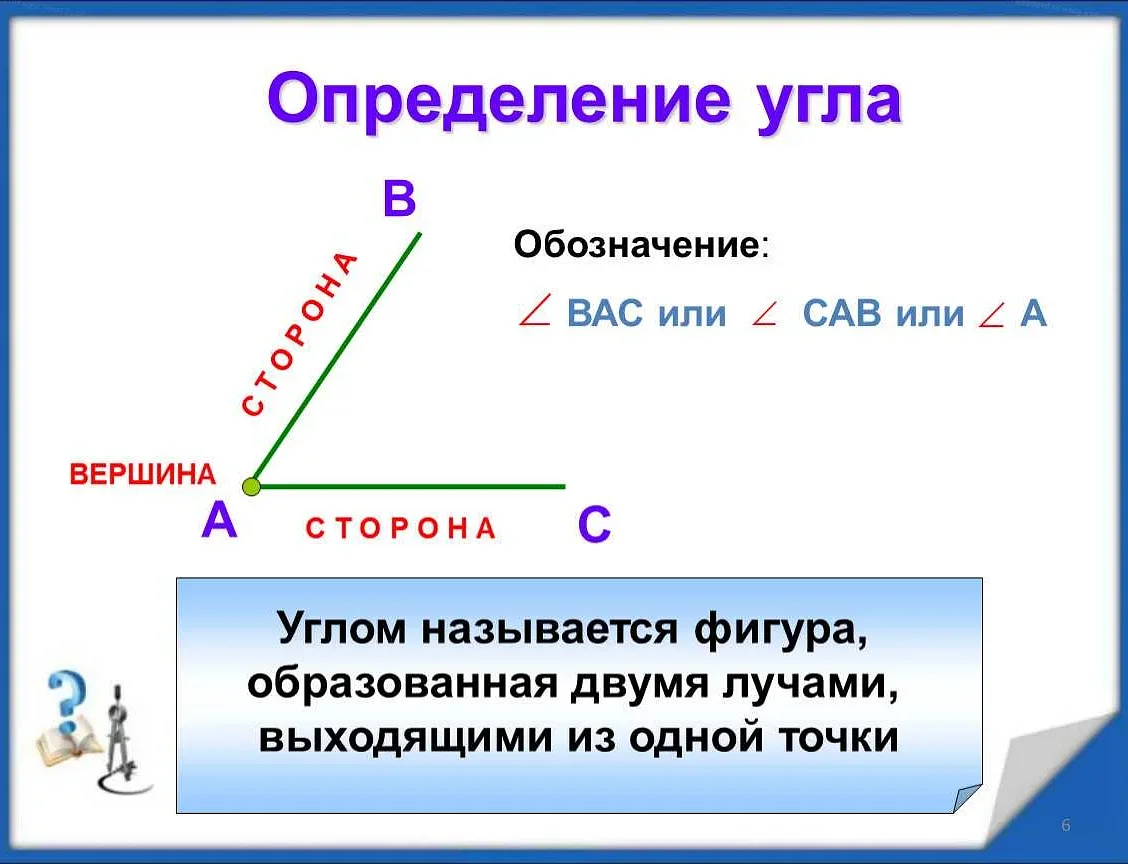
Угол альфа в математике обозначает угол, образованный двумя лучами, начало которых совпадает в вершине. Определение угла альфа включает его величину и направление, которое может быть против часовой стрелки (положительное значение) или по часовой стрелке (отрицательное значение). Угол альфа играет важную роль в геометрии и тригонометрии, и используется для измерения поворота и ориентации в пространстве.

Угол альфа – одно из ключевых понятий геометрии. В математике углы играют важную роль, и угол альфа не является исключением. Определение угла альфа включает в себя две прямые линии, называемые сторонами угла, и точку, называемую вершиной угла. Угол альфа обозначается буквой «α».

Угол альфа может быть остроугольным, прямым, тупоугольным или полным. В остроугольном угле стороны угла лежат по одну сторону от его вершины и образуют острый угол. В прямом угле стороны угла образуют прямой угол, равный 90 градусам. В тупоугольном угле стороны угла лежат по одну сторону от его вершины и образуют тупой угол, больший 90 градусов. Полный угол составляет 360 градусов и является суммой всех углов вокруг точки.

Угол альфа имеет множество свойств, которые полезны при решении геометрических задач. Например, сумма углов в треугольнике равна 180 градусам, поэтому если известны значения двух углов, можно вычислить третий. Также известно, что вертикальные углы равны между собой, а при параллельных линиях сходные углы равны между собой.

Примеры использования угла альфа в реальной жизни включают измерение угла между двумя линиями, определение направления движения объекта в пространстве и расчет площади геометрических фигур.

Определение угла альфа

Угол альфа можно представить в виде таблицы, где первый столбец содержит значения угла в градусах, второй столбец — значения угла в радианах, а третий столбец — значения угла в градусах, минутах и секундах.

Градусы (°)Радианы (рад)Градусы, минуты и секунды (° ‘ «)

0	0	0° 0′ 0″
30	π/6	30° 0′ 0″
45	π/4	45° 0′ 0″
60	π/3	60° 0′ 0″
90	π/2	90° 0′ 0″

Таким образом, угол альфа — это угол, который имеет определенное значение в градусах, радианах и градусах, минутах и секундах. Знание этих значений позволяет производить различные вычисления и применять угол альфа в различных областях математики и физики.

Типы углов альфа

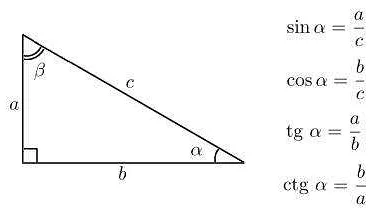
В математике существует несколько типов углов, которые могут быть обозначены символом альфа. Рассмотрим некоторые из них:

Тип углаОписание

Острый угол (α < 90°)	Угол, который меньше прямого угла (меньше 90°).
Прямой угол (α = 90°)	Угол, который равен 90° и является прямым.
Тупой угол (90° < α < 180°)	Угол, который больше прямого угла (больше 90°), но меньше полного угла (меньше 180°).
Полный угол (α = 180°)	Угол, который равен 180° и является полным.
Отрицательный угол	Угол, который отрицательный (меньше нуля) и измеряется в градусах.

Изучение углов альфа позволяет более глубоко понять геометрические фигуры и их свойства. Знание типов углов альфа помогает в решении задач и доказательств в различных областях математики.

Свойства угла альфа

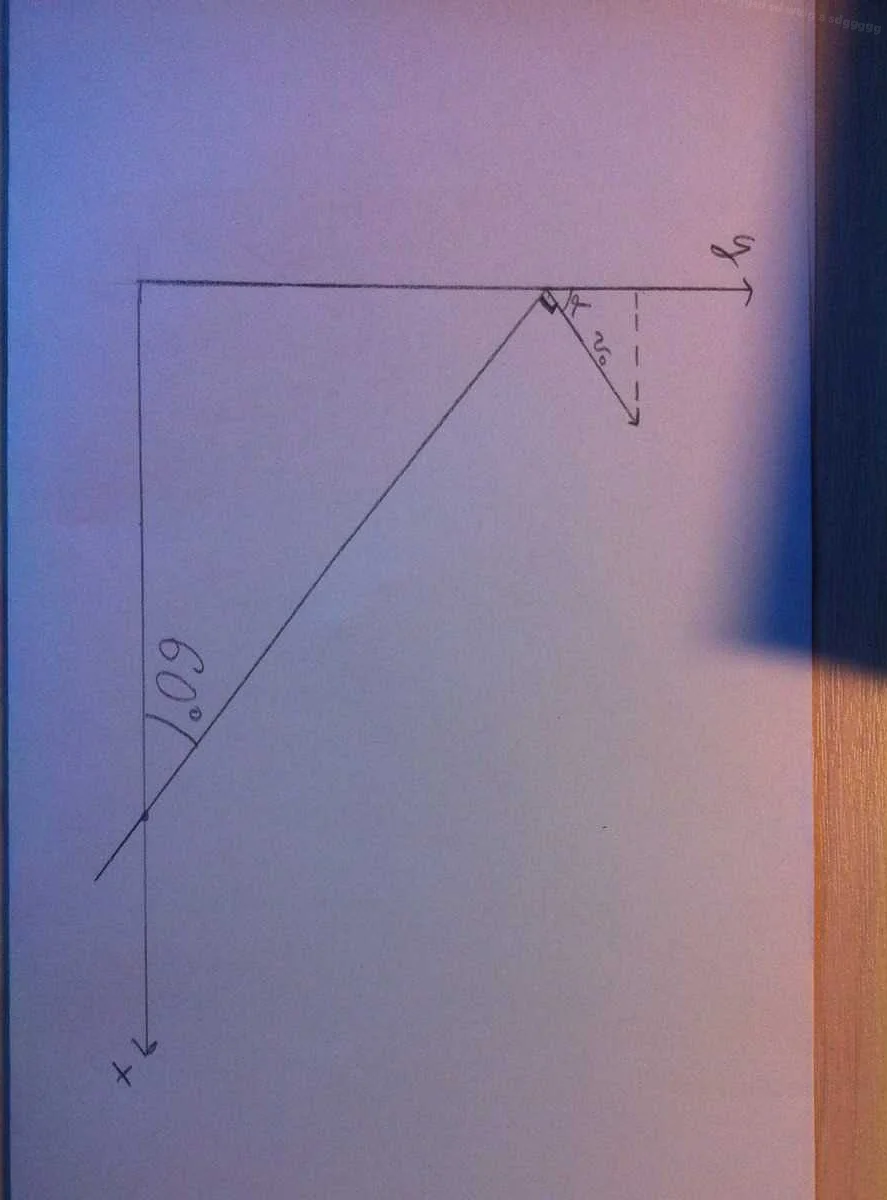
Угол альфа обладает рядом основных свойств, которые могут быть полезны при его изучении и применении в математике. Ниже приведены некоторые из этих свойств:

1. Угол альфа может быть остроугольным, прямым или тупоугольным, в зависимости от величины его меры.
2. Сумма углов альфа и его дополнения равна 180 градусам: α + (90° — α) = 180°.
3. Угол альфа и его смежные углы образуют линейную пару углов, сумма которых равна 180 градусам.
4. Угол альфа и его вертикально противоположный угол равны по величине: α = β.
5. Угол альфа и его дополнение являются смежными углами и образуют прямую линию: α + β = 180°.
6. Угол альфа и его смежный угол образуют пару комплементарных углов, сумма которых равна 90 градусам.

Это лишь некоторые из основных свойств угла альфа. Знание и понимание этих свойств позволяет использовать угол альфа в различных математических задачах и вычислениях.

Зависимость угла альфа от других углов

В геометрии угол альфа может зависеть от других углов в треугольниках, многогранниках и других геометрических фигурах. Зависимость угла альфа от других углов обусловлена геометрическими свойствами этих фигур.

В треугольнике, например, угол альфа может зависеть от двух других углов треугольника. В случае прямоугольного треугольника, сумма всех углов равна 180 градусов, поэтому если известны два угла треугольника, можно легко определить третий угол, который будет углом альфа.

В многогранниках, угол альфа может зависеть от углов, образуемых гранями этого многогранника. Например, в случае правильной пирамиды угол альфа будет зависеть от угла между основанием пирамиды и ее высотой.

Зависимость угла альфа от других углов может быть сложной и требовать применения различных геометрических свойств. Поэтому важно учиться анализировать и решать задачи, в которых требуется определить зависимость угла альфа от других углов.

Измерение угла альфа

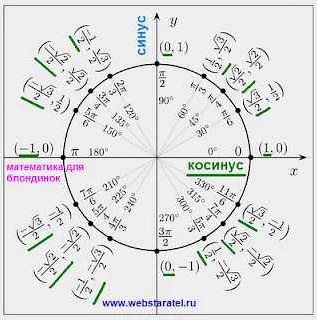
Угол альфа измеряется с использованием градусов, минут и секунд, также известных как градусная мера. Градусная мера угла альфа обычно обозначается символом °.

Угол альфа может быть измерен с точностью до минут и секунд, где 1 градус равен 60 минутам, а 1 минута равна 60 секундам. Например, угол, равный 45 градусам, 30 минутам и 15 секундам, записывается как 45° 30′ 15″.

Для измерения угла альфа можно использовать градусный траспортный круг или инструменты, основанные на градусной мере. Градусный траспортный круг представляет собой круговой инструмент, разделенный на 360 равных частей, каждая из которых соответствует 1 градусу. Он используется для измерения точного угла альфа.

Градусы (°)Минуты (‘)Секунды («)

0	0	0
30	0	0
45	0	0
60	0	0

Таким образом, угол альфа может быть измерен и записан с использованием градусной меры, что позволяет точно определить его величину.

Примеры углов альфа в геометрии

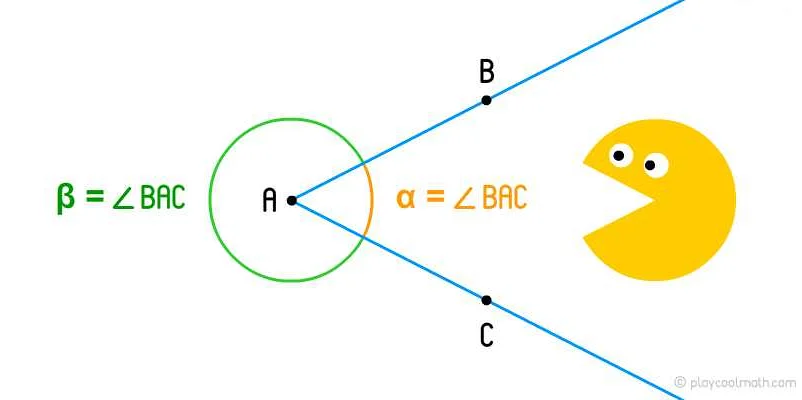
Углы альфа часто встречаются в геометрии и могут быть использованы для решения различных задач. Вот несколько примеров углов альфа:

ПримерОписание

Угол альфа в треугольнике	В треугольнике ABC угол альфа может быть определен как угол между сторонами AB и AC. Этот угол может быть использован для определения других углов и сторон треугольника.
Угол альфа в прямоугольнике	В прямоугольнике ABCD угол альфа может быть определен как угол между сторонами AB и BC. Этот угол может быть использован для определения других углов и сторон прямоугольника.
Угол альфа в круге	В круге угол альфа может быть определен как угол между радиусом и касательной, проведенной к окружности на точку касания. Этот угол может быть использован для определения других углов и отрезков в круге.

Это лишь некоторые примеры углов альфа в геометрии. В зависимости от задачи и фигуры, угол альфа может иметь различные определения и свойства.

Видео по теме:

Вопрос-ответ:

Что такое угол альфа?

Угол альфа — это угол, который имеет конкретное значение и обозначается символом α. Он является одним из элементов геометрии и используется для измерения поворота точки или линии относительно начальной позиции. Угол альфа может быть как положительным, так и отрицательным, в зависимости от направления поворота.

Как определить угол альфа?

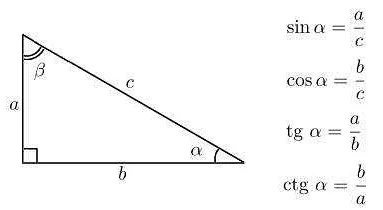
Для определения угла альфа необходимо знать начальное положение точки или линии и угол поворота относительно этого положения. Угол альфа может быть определен как количество градусов, минут и секунд поворота вокруг точки. Также он может быть выражен с помощью тригонометрических функций, таких как синус, косинус и тангенс.

Какие свойства имеет угол альфа?

Угол альфа обладает несколькими свойствами. Он может быть измерен от 0 до 360 градусов и образовывать прямой, острый или тупой угол. Угол альфа может быть суммой или разностью других углов. Также угол альфа может быть равным своему дополнению или суплементу, то есть углу, который в сумме с ним составляет 180 градусов.

Приведите примеры использования угла альфа в математике

Угол альфа используется во многих областях математики. Например, он применяется в геометрии для измерения поворотов и построения фигур. Угол альфа также находит применение в физике при расчете векторов и фазовых сдвигов. В тригонометрии угол альфа используется для определения значений тригонометрических функций и решения уравнений. Примеры использования угла альфа можно найти и в других областях науки и техники.

Какие есть альтернативные способы обозначения угла альфа?

Помимо символа α, угол альфа может быть обозначен с помощью буквы «А» или «α». Также иногда используются другие обозначения, такие как «θ» (тета) или «φ» (фи). Выбор обозначения угла альфа зависит от конкретной области математики или науки, в которой он используется.

Что такое угол альфа?

Угол альфа — это угол, обозначаемый символом α, который может быть измерен в градусах или радианах.

Примеры углов альфа в тригонометрии

В тригонометрии угол альфа (α) может быть любым углом, измеренным в радианах или градусах. Ниже приведены несколько примеров углов альфа.

Пример 1: α = 45°

Угол альфа равен 45 градусов. Это угол, который делит прямую на две равные части и имеет значение 1/8 оборота.

Пример 2: α = π/6

Угол альфа равен π/6 радиан. Это угол, который делит окружность на шесть равных секторов и имеет значение 30 градусов.

Пример 3: α = 90°

Угол альфа равен 90 градусов. Это прямой угол, который делит прямую на две перпендикулярные части и имеет значение 1/4 оборота.

Пример 4: α = π/2

Угол альфа равен π/2 радиан. Это прямой угол, который делит окружность на две равные дуги и имеет значение 90 градусов.

Это только небольшая часть примеров углов альфа, которые могут встречаться в тригонометрии. Угол альфа может принимать различные значения в зависимости от конкретной задачи или контекста использования.

Применение угла альфа в практических задачах

Угол альфа (α) широко применяется в различных практических задачах, связанных с геометрией, физикой и инженерными расчетами. Он может использоваться для определения направления, измерения углового поворота и нахождения неизвестных сторон и углов в треугольниках.

Одно из основных применений угла альфа — измерение углового поворота. Например, в авиации и навигации угол альфа может использоваться для определения угла между направлением движения самолета и локальной вертикалью. Это позволяет пилотам точно контролировать маневры и поддерживать заданный курс.

Угол альфа также может быть использован для нахождения неизвестных сторон и углов в треугольниках. Например, если известны две стороны треугольника и угол между ними, то можно использовать тригонометрические соотношения, основанные на угле альфа, для вычисления третьей стороны и других углов треугольника. Это может быть полезно в строительстве, геодезии, картографии и других областях, где требуется точное измерение и расчет геометрических параметров.

Другой пример применения угла альфа — определение направления. Например, в физике при анализе движения тела можно использовать угол альфа для определения направления силы, скорости и ускорения. Это помогает понять, какие факторы влияют на движение и как их можно контролировать.

В заключение, угол альфа имеет широкий спектр применений в практических задачах, связанных с геометрией, физикой и инженерными расчетами. Он может использоваться для измерения углового поворота, нахождения неизвестных сторон и углов в треугольниках, а также для определения направления. Понимание и использование угла альфа позволяет решать разнообразные задачи, требующие точных геометрических и физических расчетов.