Что такое волнистое равно в математике
Содержимое
- 1 Что такое волнистое равно в математике
- 1.1 Волнистое равно в математике: определение и примеры
- 1.2 Видео по теме:
- 1.3 Определение волнистого равно
- 1.4 Виды волнистого равно
- 1.5 Вопрос-ответ:
- 1.6 Примеры волнистого равно в математике
- 1.7 Свойства волнистого равно
- 1.8 Волнистое равно и операции с числами
- 1.9 Волнистое равно и геометрия
- 1.10 Практическое применение волнистого равно
Волнистая функция в математике — это функция, которая имеет вид периодических колебаний, напоминающих форму волны. Она может быть использована для моделирования различных физических явлений, таких как звук, свет или электромагнитные волны. Узнайте больше о волнистых функциях и их применении в математике.
Волнистое равно — это математическое понятие, которое описывает особый тип равенства. Волнистое равно используется для обозначения соответствия, при котором элементы находятся в определенной связи или имеют схожие характеристики, но не являются полностью идентичными.
Волнистое равно обозначается знаком «≈» (знак тильды). Этот символ указывает, что два объекта похожи или близки друг к другу, но не являются точно равными. Волнистое равно используется в различных областях математики и науки, таких как физика, химия, статистика и т. д.
Примеры использования волнистого равно:
1. В физике, волнистое равно может обозначать приближенную равномерность двух величин, например, скорость света (≈ 299,792,458 м/с).
2. В статистике, волнистое равно может обозначать приближенное значение, например, π (≈ 3,14).
3. В химии, волнистое равно может обозначать приближенное значение молярной массы, например, вода (≈ 18 г/моль).
Волнистое равно позволяет установить приближенное соответствие и сравнение между объектами, что делает его полезным инструментом для описания различных явлений и измерений.
Волнистое равно в математике: определение и примеры

Символ волнистого равно часто используется в научных и инженерных расчетах, где важно указать, что результат приближенный или округленный. Например, если мы считаем площадь круга и получаем ответ 314,15, мы можем записать его как S ≈ 314,15, чтобы показать, что это приближенное значение.
Волнистое равно также часто используется в физике, где точность вычислений может быть ограничена измерительными приборами или предположениями. Например, скорость света в вакууме обычно записывается как c ≈ 3 × 10^8 м/с, чтобы указать, что это приближенное значение.
Примеры использования волнистого равно в математике:
- Площадь круга S ≈ πr^2, где π — приближенное значение числа пи, r — радиус круга.
- Ускорение свободного падения g ≈ 9,8 м/с², где g — приближенное значение ускорения свободного падения на поверхности Земли.
- Скорость звука в воздухе v ≈ 343 м/с, где v — приближенное значение скорости звука в стандартных условиях.
Волнистое равно помогает нам указать, что значения приближенные и необходимо учитывать погрешность или ограничения измерений. Оно также позволяет нам сократить запись и упростить математические выражения, сохраняя при этом достаточную точность.
Видео по теме:
Определение волнистого равно
Волнистое равно говорит о том, что два выражения равносильны, но могут отличаться в некоторых незначительных деталях. То есть, если два выражения связаны волнистым равенством, это означает, что они имеют похожую структуру или форму, но могут различаться в значениях или некоторых дополнительных компонентах.
Волнистое равно часто используется в различных областях математики, физики, информатики и других науках. Оно помогает упростить запись и сравнение выражений, особенно в случаях, когда точное равенство не требуется или невозможно.
Примеры использования волнистого равно:
- 2~3 — это означает, что числа 2 и 3 имеют похожую структуру, но отличаются в значении.
- a+b~b+a — это означает, что выражения a+b и b+a равносильны, но могут отличаться порядком слагаемых.
- x~x+0 — это означает, что выражения x и x+0 равносильны, но могут отличаться наличием нулевого слагаемого.
Волнистое равно помогает упростить запись и сравнение выражений, а также использование алгоритмов и методов, которые требуют только равносильных выражений, но не точного равенства.
Виды волнистого равно
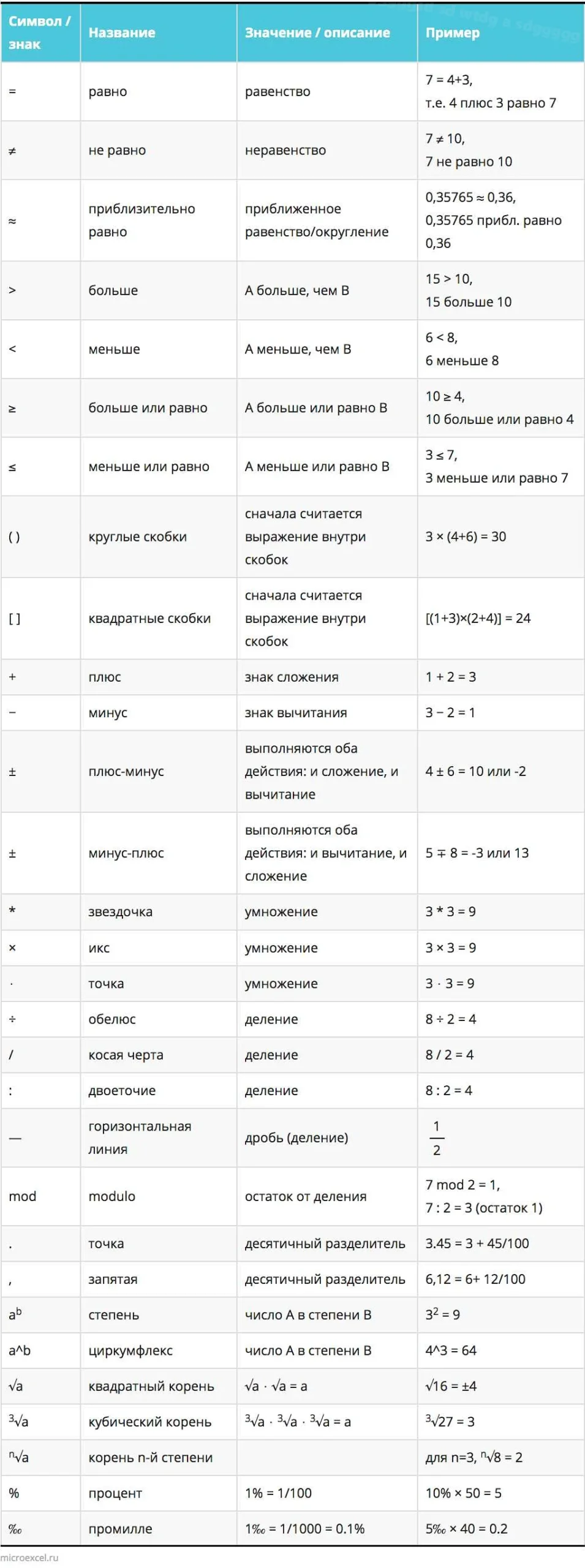
Волнистое равно имеет несколько различных видов, которые могут быть использованы в математике. Рассмотрим некоторые из них:
Вид волнистого равноПример
| ~ | 3~5 |
| ≈ | π≈3.14 |
| ≃ | 10≃11 |
| ≅ | AB≅CD |
Все эти виды волнистого равно обозначают некоторое сходство, приближение или равенство между элементами или значениями. Например, символ ~ может использоваться для обозначения примерного равенства, символ ≈ — для обозначения приближенного равенства, символы ≃ и ≅ — для обозначения сходства или равенства в некоторых геометрических или алгебраических контекстах.
Вопрос-ответ:
Что такое волнистое равно в математике?
Волнистое равно – это символ, обозначающий нестрогое равенство между двумя выражениями. Оно используется, когда два выражения могут быть равны, но не на всех значениях переменных или не во всех случаях.
Какой символ используется для обозначения волнистого равно в математике?
Волнистое равно обозначается символом ≈ (тильда с двумя линиями сверху). Этот символ показывает, что два выражения примерно равны, но не совсем точно.
Как использовать волнистое равно в математических уравнениях?
Волнистое равно применяется для указания приближенного или нестрогого равенства. Например, можно написать 1/3 ≈ 0.333, чтобы показать, что дробь 1/3 приближенно равна десятичной дроби 0.333.
Какие примеры можно привести с использованием волнистого равно?
Примеры использования волнистого равно в математике: 2π ≈ 6.283 (приближенное значение числа π), 10! ≈ 3628800 (приближенное значение факториала числа 10), sin(30°) ≈ 0.5 (приближенное значение синуса угла 30 градусов).
Примеры волнистого равно в математике

Волнистое равно (≈) используется в математике для обозначения приближенного равенства между двумя величинами. Оно означает, что две величины очень близки друг к другу, но не равны в строгом смысле.
Ниже приведены некоторые примеры использования волнистого равно:
ПримерОбъяснение
| π ≈ 3.14 | Число π (пи) приближенно равно 3.14, которое является его приближенным значением с округлением. |
| √2 ≈ 1.41 | Квадратный корень из 2 приближенно равен 1.41, что является его приближенным значением с округлением. |
| e ≈ 2.71828 | Число e (экспонента) приближенно равно 2.71828, которое является его приближенным значением с округлением. |
Волнистое равно позволяет указать, что две величины очень близки друг к другу, но не являются точно равными. Это особенно полезно при работе с приближенными значениями, округлениями и аппроксимациями в математике.
Свойства волнистого равно

1. Рефлексивность: Для любого числа а, а = а.
2. Симметричность: Если а = b, то b = а.
3. Транзитивность: Если а = b и b = с, то а = с.
4. Операции с волнистым равно: Волнистое равно можно использовать в математических операциях, таких как сложение, вычитание, умножение и деление.
5. Применение волнистого равно: Волнистое равно используется для сравнения чисел или выражений, когда результаты могут быть приближенными или неизвестными.
6. Примеры использования:
Пример 1:
Если а = 5 и b = 5.00001, то а ≈ b (приближенно равно).
Пример 2:
Если а = 10 и b = 9.9999, то а ≈ b (приближенно равно).
Пример 3:
Если а = 3 и b = 4, то а ≠ b (не равно).
Волнистое равно и операции с числами
Волнистое равно может быть использовано в различных операциях с числами. Например, в сложении и вычитании чисел, если результат приблизительно равен некоторому значению, мы можем использовать символ ≈, чтобы указать, что числа равны с некоторой погрешностью.
Например, если у нас есть два числа: 3,14159 и 3,14, мы можем записать их сложение как 3,14159 + 3,14 ≈ 6,28159. В данном случае, символ ≈ указывает, что точный результат равен 6,28159 с некоторой погрешностью.
Также, волнистое равно может быть использовано в умножении и делении чисел. Например, если у нас есть число π (пи) и мы хотим найти его приближенное значение, мы можем записать это как π ≈ 3,14. В данном случае, символ ≈ указывает, что значение числа π приближенно равно 3,14.
Волнистое равно широко используется в научных и инженерных расчетах, где точность является важным фактором. Он позволяет указать приближенное значение числа без необходимости уточнять его точность или округлять результаты.
Волнистое равно и геометрия

Волнистое равно также применяется в геометрии для обозначения отрезка, длина которого соответствует длине другого отрезка, но с некоторой волнистой формой.
Этот символ часто используется в геометрических задачах, когда необходимо указать, что два отрезка равны по длине, но имеют различную форму. Например, если нужно сравнить длину прямых отрезков AB и CD, и их длины равны, то можно записать: AB ≈ CD, где символ волнистого равно указывает на то, что форма отрезков может быть различной, но их длины совпадают.
| AB | CD |
| — | ~~~~~ |
Практическое применение волнистого равно

Область примененияПример
| Физика | Волнистое равно используется для описания колебаний и волн в физических системах. Например, при изучении звуковых волн, световых волн и электромагнитных волн. |
| Электротехника | Волнистое равно применяется при анализе электрических сигналов и передаче информации. Например, при проектировании антенн и радиосвязи. |
| Квантовая механика | Волнистое равно является основой для описания квантовых частиц и их поведения в микромире. Например, при изучении волновой функции и интерференции. |
| Финансовые рынки | Волнистое равно может использоваться для анализа финансовых рынков и прогнозирования трендов. Например, при применении технического анализа и волнового анализа. |
Это только некоторые примеры применения волнистого равно. В общем, это понятие играет важную роль в понимании и анализе различных явлений и процессов, где наблюдаются колебания и волны.


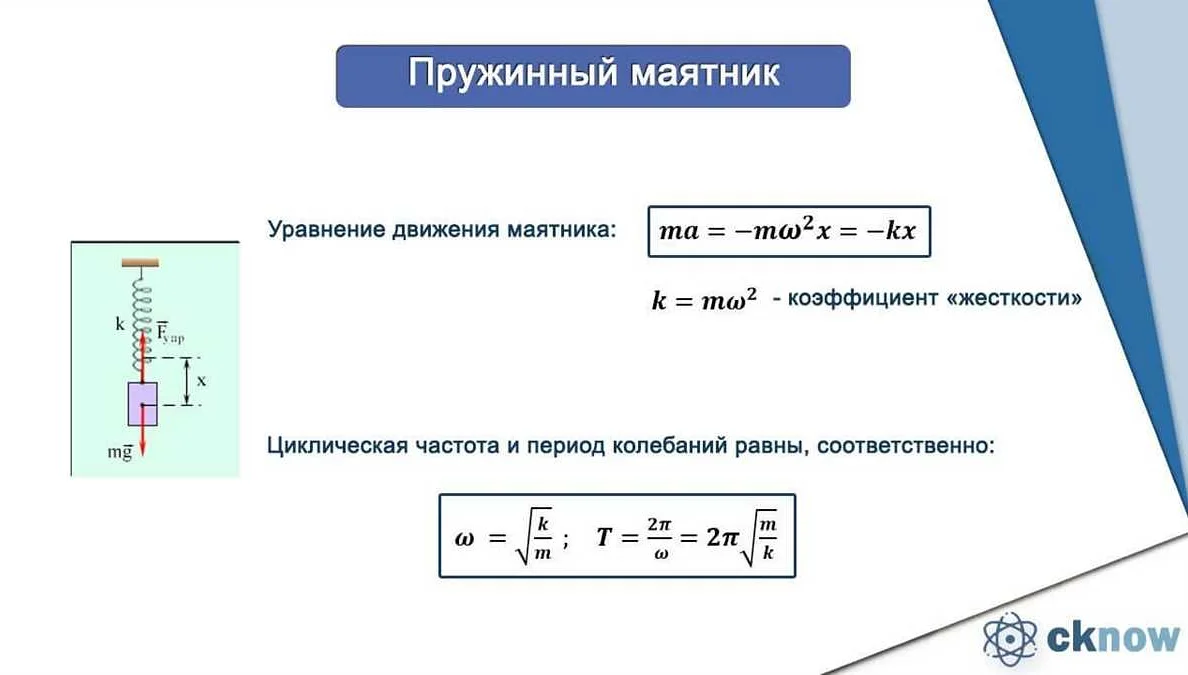

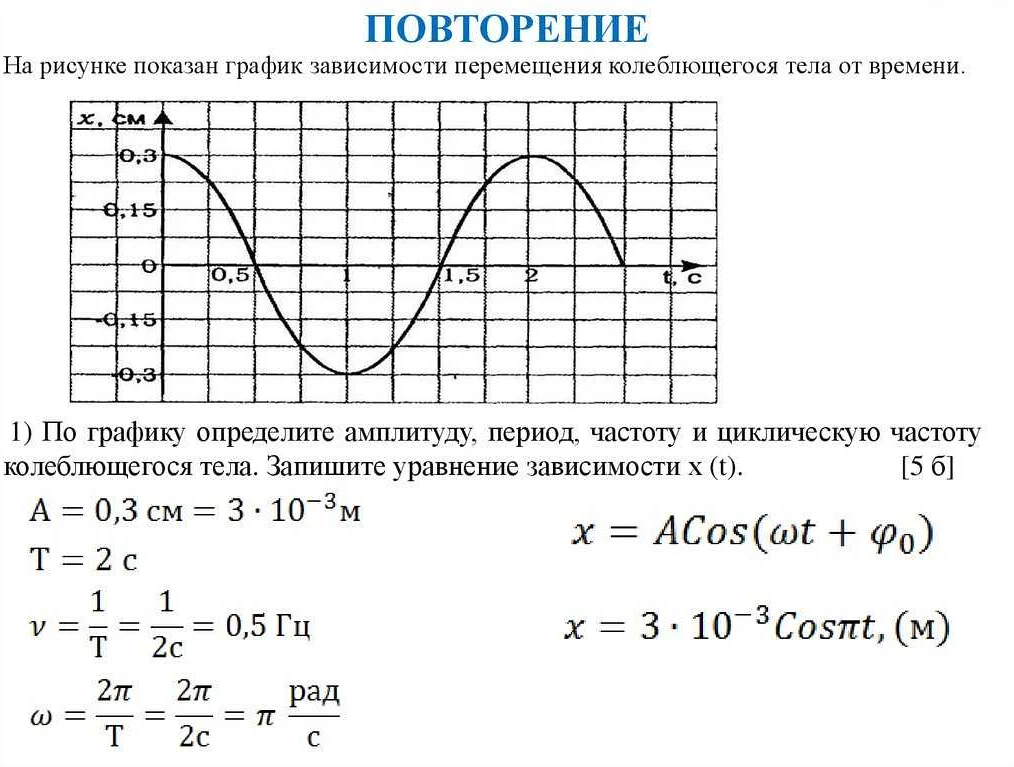
Волнистая функция, или функция с волнистым равно, является одним из важных понятий в математике. Она характеризуется периодическими колебаниями, при которых значения функции сначала возрастают, затем убывают и так далее. Волнистое равно можно встретить в различных областях математики и физики, таких как теория вероятностей, анализ и теория чисел. Примером волнистого равно может служить синусоида. Эта функция имеет периодический характер и представляет собой график колебаний. Например, если мы рассмотрим график синусоиды, то увидим, что значения функции сначала возрастают от -1 до 1, затем убывают от 1 до -1 и так далее. Волнистое равно имеет множество применений. Например, оно может использоваться для моделирования колебаний в физике и инженерии, для анализа временных рядов в экономике и финансах, а также для решения задач в теории вероятностей. В заключение, волнистое равно представляет собой важное понятие в математике, которое имеет широкий спектр применений. Изучение этого понятия позволяет лучше понять и описывать различные виды колебаний и изменений в различных системах.
Волнистые равни – это один из самых интересных и захватывающих разделов математики. Я всегда любил математику, и вот наконец-то я узнал, что такое волнистое равно! Это такой вид равенства, когда две математические формулы или выражения равны друг другу с точностью до волнистых скобок. Волнистые скобки обозначают, что значения внутри них могут быть различными, но все равно считаются равными. Просто представьте, сколько возможностей и вариантов открывается с использованием волнистого равно! Например, если у нас есть уравнение «x = 2 + 3 ~ 5», это означает, что x может быть равным значению от 2 до 5. Волнистые равни могут использоваться в самых разных областях математики, начиная от алгебры и заканчивая теорией вероятностей. Я восхищаюсь этим концептом и с нетерпением жду возможности применить его в настоящей жизни!
Статья очень понравилась, так как я всегда интересовалась математикой и ее приложениями. Волнистое равно — это понятие, которое раньше я не встречала. Очень интересно узнать, что оно означает и как оно применяется. Я рада, что статья содержит определение и примеры, так это помогает лучше понять материал. Теперь у меня возникло желание изучить эту тему более подробно. Спасибо автору за информативную и понятную статью! Жду с нетерпением новые материалы по математике.