От чего зависит период колебаний математического пружинного маятника

Период колебаний математического пружинного маятника зависит от его массы, жесткости пружины и длины маятника. Чем больше масса и жесткость пружины, и чем меньше длина маятника, тем короче будет период колебаний.

Математический пружинный маятник является одним из простейших измерительных устройств, широко применяемых в научных и инженерных расчетах. Его период колебаний — один из основных параметров, определяющих его характеристики и функциональность.

Период колебаний математического пружинного маятника зависит от нескольких факторов. В первую очередь, это масса маятника и его жесткость. Чем больше масса, тем больше период колебаний. С другой стороны, чем выше жесткость пружины, тем меньше период колебаний. Эти два фактора взаимосвязаны и определяют основные свойства маятника.

Также важным фактором, влияющим на период колебаний, является длина маятника. Чем длиннее маятник, тем меньше будет его период колебаний. Это связано с увеличением пути, который должен пройти маятник за одну полную колебательную волну. Чем длиннее путь, тем больше времени потребуется для его прохождения и, следовательно, тем больше будет период колебаний.

Формула расчета периода колебаний математического пружинного маятника выглядит следующим образом:

T = 2π√(m/k)

Где T — период колебаний, m — масса маятника, k — жесткость пружины.

Таким образом, для расчета периода колебаний математического пружинного маятника необходимо знать его массу и жесткость пружины. Этот параметр является важным при проектировании и использовании маятников в различных областях науки и техники.

Формула расчета периода колебаний математического пружинного маятника

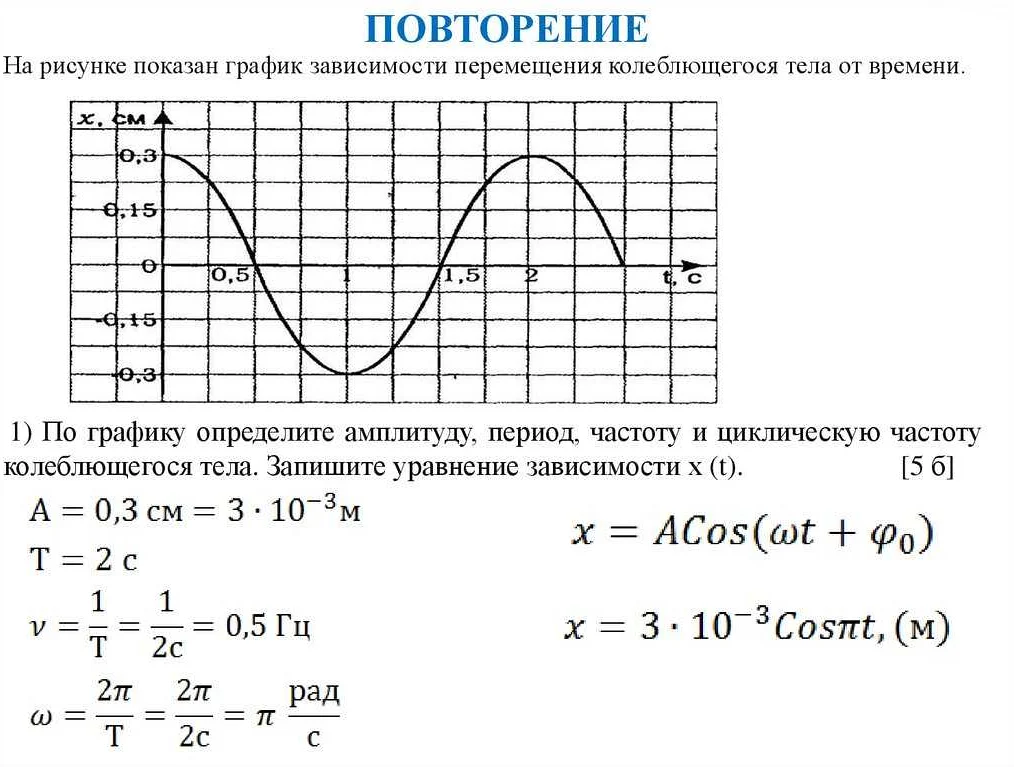
Период колебаний математического пружинного маятника зависит от нескольких факторов, таких как масса груза, жесткость пружины и длина маятника. Формула для расчета периода колебаний данного маятника может быть записана следующим образом:

T = 2π√(m/k)

где:

• T — период колебаний;
• π — математическая константа, примерно равная 3.14159;
• m — масса груза, подвешенного на пружине;
• k — жесткость пружины.

В данной формуле период колебаний обратно пропорционален квадратному корню из отношения массы груза к жесткости пружины. Более тяжелый груз или жестче пружина будут приводить к более медленным колебаниям, в то время как более легкий груз или менее жесткая пружина будут вызывать более быстрые колебания.

Зависимость периода колебаний от массы маятника

T = 2π√(m/k)

где:

• T — период колебаний;
• π — число пи (приближенное значение 3,14159);
• m — масса маятника;
• k — жесткость пружины.

Из формулы видно, что период колебаний обратно пропорционален корню из массы маятника. То есть, с увеличением массы маятника, период колебаний увеличивается. Это связано с тем, что большая масса требует больше времени для прохождения полного колебания.

Важно отметить, что зависимость периода колебаний от массы маятника является идеализированной и справедлива только при условии, что длина пружины и сила сопротивления воздуха остаются постоянными.

Влияние длины пружины на период колебаний

Чем длиннее пружина, тем меньше ее жесткость. Жесткость пружины характеризует ее способность сопротивляться деформации. Если пружина жесткая, то период колебаний будет меньше. Если пружина мягкая, то период колебаний будет больше.

Математически формула для расчета периода колебаний математического пружинного маятника выглядит следующим образом:

T = 2π√(m/k)

где:

• T — период колебаний;
• π — число «пи» (примерное значение 3,14);
• m — масса тела, подвешенного на пружине;
• k — жесткость пружины.

Из этой формулы видно, что период колебаний обратно пропорционален квадратному корню из жесткости пружины. Таким образом, увеличение длины пружины приведет к увеличению периода колебаний, а уменьшение длины — к уменьшению периода колебаний.

Роль жесткости пружины в колебаниях математического маятника

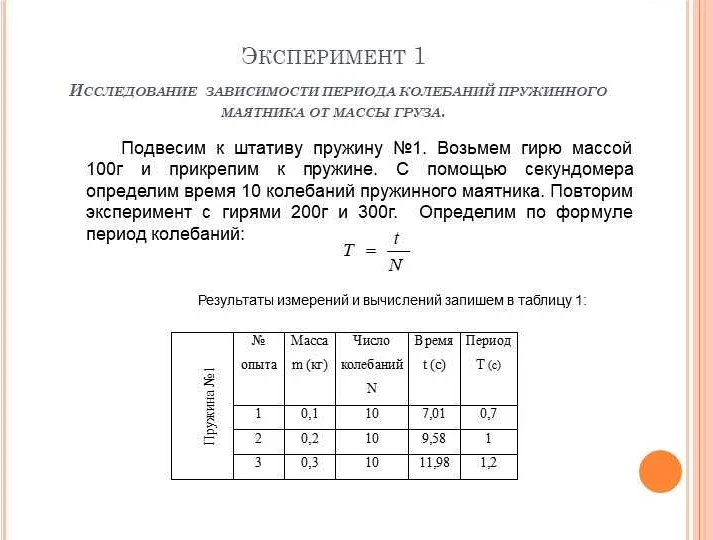
Период колебаний математического маятника зависит от массы маятника и его жесткости. Чем жестче пружина, тем быстрее будет происходить колебание маятника. Это связано с тем, что жесткая пружина будет возвращать маятник к равновесному положению с большей силой, чем более мягкая пружина.

Формула расчета периода колебаний математического пружинного маятника включает в себя коэффициент жесткости пружины:

Т = 2π√(m/k),

где T — период колебаний, m — масса маятника, k — коэффициент жесткости пружины.

Таким образом, жесткость пружины играет важную роль в определении периода колебаний математического маятника. Изменение жесткости пружины может привести к изменению скорости и амплитуды колебаний маятника.

Взаимосвязь между силой упругости пружины и периодом колебаний

Взаимосвязь между силой упругости пружины и периодом колебаний можно выразить формулой:

ФормулаОписание

T = 2π√(m/k)

Формула для расчета периода колебаний пружинного маятника

где:

• T — период колебаний (время, за которое маятник совершает одно полное колебание)
• π — математическая константа, примерно равная 3.14159
• m — масса подвеса (масса, которая находится на конце пружины)
• k — жесткость пружины (коэффициент, характеризующий ее упругие свойства)

Из формулы видно, что период колебаний математического пружинного маятника обратно пропорционален корню из жесткости пружины. То есть, чем жестче пружина, тем меньше будет период колебаний, и наоборот.

Таким образом, сила упругости пружины напрямую влияет на ее жесткость, а значит, и на период колебаний математического пружинного маятника. При увеличении силы упругости пружины, жесткость пружины увеличивается, а период колебаний сокращается. И наоборот, при уменьшении силы упругости пружины, жесткость пружины уменьшается, а период колебаний увеличивается.

Понимание взаимосвязи между силой упругости пружины и периодом колебаний помогает в расчетах и проектировании математических пружинных маятников, а также позволяет оптимизировать их характеристики для конкретных задач.

Как масса груза влияет на период колебаний пружинного маятника

В соответствии с законом Гука, период колебаний пружинного маятника прямо пропорционален квадратному корню из массы груза и обратно пропорционален жесткости пружины. Формула для расчета периода колебаний пружинного маятника выглядит следующим образом:

T = 2π√(m/k)

Здесь T — период колебаний, m — масса груза, k — жесткость пружины.

Из этой формулы видно, что увеличение массы груза приводит к увеличению периода колебаний. Это означает, что маятник будет затрачивать больше времени на прохождение полного цикла движения. Следовательно, при увеличении массы груза пружинный маятник будет колебаться медленнее.

Это связано с тем, что увеличение массы груза приводит к увеличению инерции системы, а значит, требуется больше силы для изменения направления движения маятника. Это приводит к увеличению периода колебаний.

Таким образом, масса груза является важным фактором, который влияет на период колебаний пружинного маятника. При увеличении массы груза период колебаний увеличивается, а маятник колеблется медленнее.

Формула расчета периода колебаний математического пружинного маятника

Другим важным фактором является жесткость пружины, которая обозначается символом k. Жесткость пружины определяет, насколько сильно пружина будет сопротивляться изменению своей длины при приложении силы к маятнику.

Формула для расчета периода колебаний математического пружинного маятника выглядит следующим образом:

T = 2π√(m/k)

где T — период колебаний, π — математическая константа «пи» (приблизительно 3.14159), m — масса маятника и k — жесткость пружины.

Из данной формулы видно, что период колебаний обратно пропорционален корню из отношения массы маятника к его жесткости. Таким образом, с увеличением массы маятника или уменьшением жесткости пружины, период колебаний будет увеличиваться.

Влияние сопротивления воздуха на период колебаний

Сопротивление воздуха приводит к постепенному затуханию колебаний маятника. Это происходит из-за диссипации энергии, которая тратится на преодоление силы сопротивления воздуха. С увеличением сопротивления воздуха, период колебаний становится больше, так как меньше энергии остается для самого движения.

Формула для расчета периода колебаний математического пружинного маятника с учетом сопротивления воздуха имеет вид:

T = 2π√(m/k + b²/4m²)

где T — период колебаний, m — масса маятника, k — коэффициент жесткости пружины, b — коэффициент сопротивления воздуха.

Таким образом, сопротивление воздуха увеличивает период колебаний математического пружинного маятника, так как уменьшает энергию, доступную для движения.

Особенности периода колебаний математического пружинного маятника в разных условиях

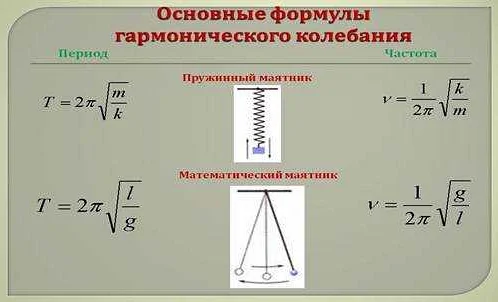
Период колебаний математического пружинного маятника зависит от нескольких факторов, в том числе от массы маятника, жесткости пружины и амплитуды колебаний. Однако, помимо этих основных параметров, период колебаний может быть также повлиян различными условиями, в которых находится маятник.

Рассмотрим несколько особенностей периода колебаний математического пружинного маятника в разных условиях:

УсловиеОписание

Гравитационное поле	В условиях сильного гравитационного поля, период колебаний будет меньше, чем в условиях слабого гравитационного поля. Это связано с тем, что сила тяжести влияет на возвращающую силу пружины.
Температура	При изменении температуры, жесткость пружины может меняться, что в свою очередь повлияет на период колебаний. С увеличением температуры жесткость пружины возрастает, что приводит к увеличению периода колебаний.
Сопротивление среды	В условиях высокого сопротивления среды, период колебаний будет больше, чем в условиях низкого сопротивления. Это связано с тем, что сопротивление среды затухает колебания маятника, что приводит к увеличению периода.
Внешние силы	Если на математический пружинный маятник действуют внешние силы, такие как ветер или вибрации, то это может повлиять на период колебаний маятника. Внешние силы могут изменить амплитуду колебаний и, следовательно, период колебаний.

Таким образом, период колебаний математического пружинного маятника не только зависит от основных параметров, но и может быть изменен различными условиями, в которых находится маятник. При расчете периода колебаний необходимо учитывать все эти факторы для получения более точных результатов.

Вопрос-ответ:

От чего зависит период колебаний математического пружинного маятника?

Период колебаний математического пружинного маятника зависит от нескольких факторов: массы груза, жесткости пружины и длины маятника.

Какая формула позволяет рассчитать период колебаний математического пружинного маятника?

Формула для расчета периода колебаний математического пружинного маятника выглядит следующим образом: T = 2π√(m/k), где T — период колебаний, m — масса груза, k — жесткость пружины.

Как влияет масса груза на период колебаний математического пружинного маятника?

Масса груза влияет на период колебаний математического пружинного маятника обратно пропорционально — чем больше масса груза, тем меньше период колебаний.

Как жесткость пружины влияет на период колебаний математического пружинного маятника?

Жесткость пружины влияет на период колебаний математического пружинного маятника прямо пропорционально — чем жестче пружина, тем меньше период колебаний.

От каких еще факторов может зависеть период колебаний математического пружинного маятника?

Помимо массы груза и жесткости пружины, период колебаний математического пружинного маятника может зависеть от амплитуды колебаний, наличия дополнительных сил трения или сопротивления воздуха.

Какие факторы влияют на период колебаний математического пружинного маятника?

Период колебаний математического пружинного маятника зависит от нескольких факторов. Во-первых, он зависит от массы маятника. Чем больше масса, тем больше период колебаний. Во-вторых, период колебаний зависит от жесткости пружины. Чем жестче пружина, тем меньше период колебаний. И, наконец, период колебаний также зависит от длины пружины. Чем длиннее пружина, тем больше период колебаний. Формула для расчета периода колебаний математического пружинного маятника выглядит следующим образом: T = 2 * π * √(m/k), где T — период колебаний, m — масса маятника, k — жесткость пружины.

Какая формула используется для расчета периода колебаний математического пружинного маятника?

Для расчета периода колебаний математического пружинного маятника используется следующая формула: T = 2 * π * √(m/k), где T — период колебаний, m — масса маятника, k — жесткость пружины. Эта формула учитывает зависимость периода колебаний от массы маятника и жесткости пружины. Чем больше масса маятника, тем больше период колебаний, а чем жестче пружина, тем меньше период колебаний. Также стоит отметить, что период колебаний не зависит от амплитуды колебаний или начальной скорости маятника.

Видео по теме: