Что такое x2 в математике

x2 в математике обозначает возведение числа в квадрат. Это означает, что число умножается само на себя. Узнайте больше о квадрате числа и его свойствах.

В математике, символ x2 обозначает квадрат числа. Квадрат числа — это результат умножения числа на само себя. Например, квадрат числа 5 равен 5 умножить на 5, что равно 25.

Символ x2 можно использовать и для переменных. Например, если у нас есть переменная a и мы хотим возвести ее в квадрат, то мы можем записать это как a x2. Это означает, что переменная a будет умножена сама на себя.

Квадрат числа имеет множество применений в математике. Один из наиболее распространенных примеров — нахождение площади квадрата. Площадь квадрата можно найти, умножив длину его стороны на саму себя, то есть возвести длину стороны в квадрат, что можно записать как s2, где s — длина стороны квадрата.

В общем, символ x2 в математике означает возведение числа или переменной в квадрат. Это понятие имеет широкое применение в различных математических задачах, включая нахождение площади, объема и других.

Что такое x2 в математике

В математике символ x2 обозначает квадрат числа x. Квадрат числа получается путем умножения числа на само себя. Таким образом, x2 равно произведению числа x на само себя.

Например, если x = 2, то x2 будет равным 2 * 2 = 4. Если x = -3, то x2 будет равным (-3) * (-3) = 9. Также можно записать x2 в виде x * x или как x в квадрате.

Квадрат числа x используется в различных областях математики и естественных науках. Например, в геометрии квадрат числа x соответствует площади квадрата со стороной x. В физике квадрат числа x может представлять квадрат скорости, ускорения или других физических величин.

Квадрат числа x также является важной математической операцией и используется в различных алгебраических выражениях и уравнениях. Например, в квадратном уравнении x2 + 2x + 1 = 0, x2 представляет квадратный член, который содержит переменную x во второй степени.

В таблице ниже приведены некоторые примеры значений x и соответствующих значений x2:

xx2

0	0
1	1
2	4
3	9
-1	1
-2	4
-3	9

Таким образом, x2 в математике означает квадрат числа x, который является результатом умножения числа на само себя.

Определение

В математике символ «x2» обозначает возведение числа в квадрат или умножение числа на само себя. Это математическое действие позволяет получить квадрат числа, то есть результат умножения числа на себя.

Например, если имеется число 5, то 5 в квадрате обозначается как 52 и равно 25 (5 * 5 = 25). Аналогично, число -3 в квадрате, обозначается как (-3)2 и равно 9 ((-3) * (-3) = 9).

В математике символ «x2» часто используется для нахождения площадей фигур, таких как квадраты или прямоугольники. Например, для нахождения площади квадрата со стороной 4, необходимо возвести длину стороны в квадрат: 42 = 16.

Понятие x2 в математике

Квадрат числа x можно представить в виде x * x или x2. Здесь x — это значение числа, которое мы возводим в квадрат.

Операция возведения в квадрат широко используется в математике и других областях, таких как физика и технические науки. Например, квадраты чисел используются для вычисления площадей квадратных фигур и для решения квадратных уравнений.

Кроме того, операция возведения в квадрат имеет много свойств и правил, которые помогают упростить вычисления. Например, квадрат суммы двух чисел равен сумме квадратов этих чисел: (a + b)2 = a2 + 2ab + b2.

Возведение в квадрат является важным понятием в математике и имеет множество применений в реальном мире. Понимание этой операции позволяет нам решать различные задачи и упрощать вычисления.

Свойства

В математике x2 обладает несколькими важными свойствами:

1. Свойство коммутативности:	x2 можно менять местами: a2 = 2a.
2. Свойство ассоциативности:	Умножение x2 ассоциативно: (a2)2 = a4.
3. Свойство дистрибутивности:	x2 можно раскрывать по формуле: (a + b)2 = a2 + 2ab + b2.
4. Свойство нейтрального элемента:	Если a = 1, то a2 = 1.

Эти свойства позволяют использовать x2 в различных математических операциях и упрощать выражения.

Основные характеристики x2

Основные характеристики x2:

• x2 является операцией возведения числа в квадрат;
• Знак x2 показывает, что число нужно умножить само на себя;
• Например, если x = 3, то x2 = 3 * 3 = 9;
• Число, возведенное в квадрат, всегда положительное или ноль, так как умножение положительных или отрицательных чисел на себя дает положительный результат;
• x2 можно использовать для вычисления площадей фигур, например, квадратов или прямоугольников;
• x2 также может быть использован в алгебре, геометрии и физике для задания и решения различных задач.

Использование x2 в математике позволяет работать с числами и вычислять различные значения, а также решать задачи из различных областей науки и практики.

Примеры использования

Другой пример использования x2 — решение квадратного уравнения. Квадратный корень известен как x2. Например, если у нас есть квадратное уравнение x2 — 4x + 4 = 0, то его решением будет x = 2.

Также x2 может использоваться в выражении для обозначения повторяющихся операций. Например, если у нас есть выражение (2 + 3) x 2, то его можно записать как (2 + 3)2 = 25.

xx2

1	1
2	4
3	9

Как видно из таблицы, если число умножить на себя (x2), то получится квадрат этого числа.

Примеры задач с x2

Рассмотрим несколько примеров задач, где использование x2 в математике может быть полезным:

1. Найти площадь квадрата со стороной x2. Для этого нужно умножить значение x2 на само себя: S = x2 * x2 = x4.
2. Решить квадратное уравнение вида ax2 + bx + c = 0. Здесь x2 обозначает переменную, которую нужно найти. Решение уравнения может включать два, одно или ни одного значения x2.
3. Определить объем куба со стороной x2. Для этого нужно возвести значение x2 в куб: V = (x2)3 = x6.
4. Вычислить площадь поверхности сферы с радиусом x2. Для этого нужно использовать формулу S = 4πr2, где r — радиус сферы.
5. Решить систему уравнений, содержащую переменные x и y, в которых есть степени x2 и y2. В таких случаях нужно использовать методы решения системы уравнений, подходящие для квадратных уравнений.

Это лишь некоторые примеры задач, где использование x2 в математике может быть полезным. В общем случае, x2 используется для обозначения возведения числа в квадрат и может применяться в различных задачах и формулах.

Графики и графы

Графиком называется визуальное представление функции или зависимости одной переменной от другой. График позволяет наглядно представить изменение значений переменных и их взаимосвязь.

График может быть построен на координатной плоскости, где оси называются абсциссой и ординатой. Значения переменных откладываются на соответствующие осям, после чего точки соединяются линиями. Таким образом, можно увидеть, как меняется переменная в зависимости от значения другой переменной.

Графики широко используются в различных областях, таких как математика, физика, экономика и т. д. Они позволяют исследовать различные зависимости и делать выводы о характере взаимодействия переменных.

Графом называется абстрактная структура данных, состоящая из вершин и ребер, которые соединяют вершины. Вершины представляют собой объекты, а ребра — связи между ними. Графы широко используются в теории графов и компьютерных науках.

Графы могут иметь различную структуру и быть направленными или ненаправленными. Они используются для моделирования и анализа различных систем и сетей, таких как социальные сети, транспортные сети, сети связи и т. д.

В математике графы используются для изучения свойств и алгоритмов на графах, таких как поиск кратчайшего пути, построение минимального остовного дерева и т. д. Они являются мощным инструментом для решения сложных задач и анализа структуры данных.

Видео по теме:

Вопрос-ответ:

Что такое x2 в математике?

x2 в математике означает возведение числа в квадрат. Это процесс, при котором число умножается само на себя. Например, 5 в квадрате равно 5 * 5 = 25.

Как использовать x2 в математике?

x2 может использоваться для решения различных задач и вычислений. Например, если нам нужно найти площадь квадрата со стороной 2, мы можем возвести это число в квадрат: 2 * 2 = 4. Таким образом, площадь квадрата будет равна 4.

Какие еще примеры использования x2 в математике?

x2 может быть использовано для нахождения площади прямоугольника. Если у нас есть прямоугольник с длиной стороны 3 и шириной стороны 4, мы можем возвести обе стороны в квадрат и затем перемножить полученные числа: 3 * 3 = 9 и 4 * 4 = 16. Затем мы складываем эти два результата: 9 + 16 = 25. Таким образом, площадь прямоугольника будет равна 25.

Можно ли использовать x2 с отрицательными числами?

Да, x2 можно использовать и с отрицательными числами. В этом случае, когда число возводится в квадрат, знак минуса остается, но становится положительным. Например, (-2) в квадрате равно (-2) * (-2) = 4.

Какую роль играет x2 в алгебре?

x2 в алгебре может быть использовано для решения уравнений и нахождения неизвестных значений. Например, если у нас есть уравнение x2 = 9, мы можем найти значение x, возведя обе стороны уравнения в квадратный корень: x = ±√9 = ±3. Таким образом, решением уравнения будет x = 3 или x = -3.

Что такое x2 в математике?

x2 в математике обозначает возведение числа в квадрат. Это значит, что число умножается само на себя. Например, 3 в квадрате равно 3 * 3 = 9.

Отражение x2 на графиках и графах

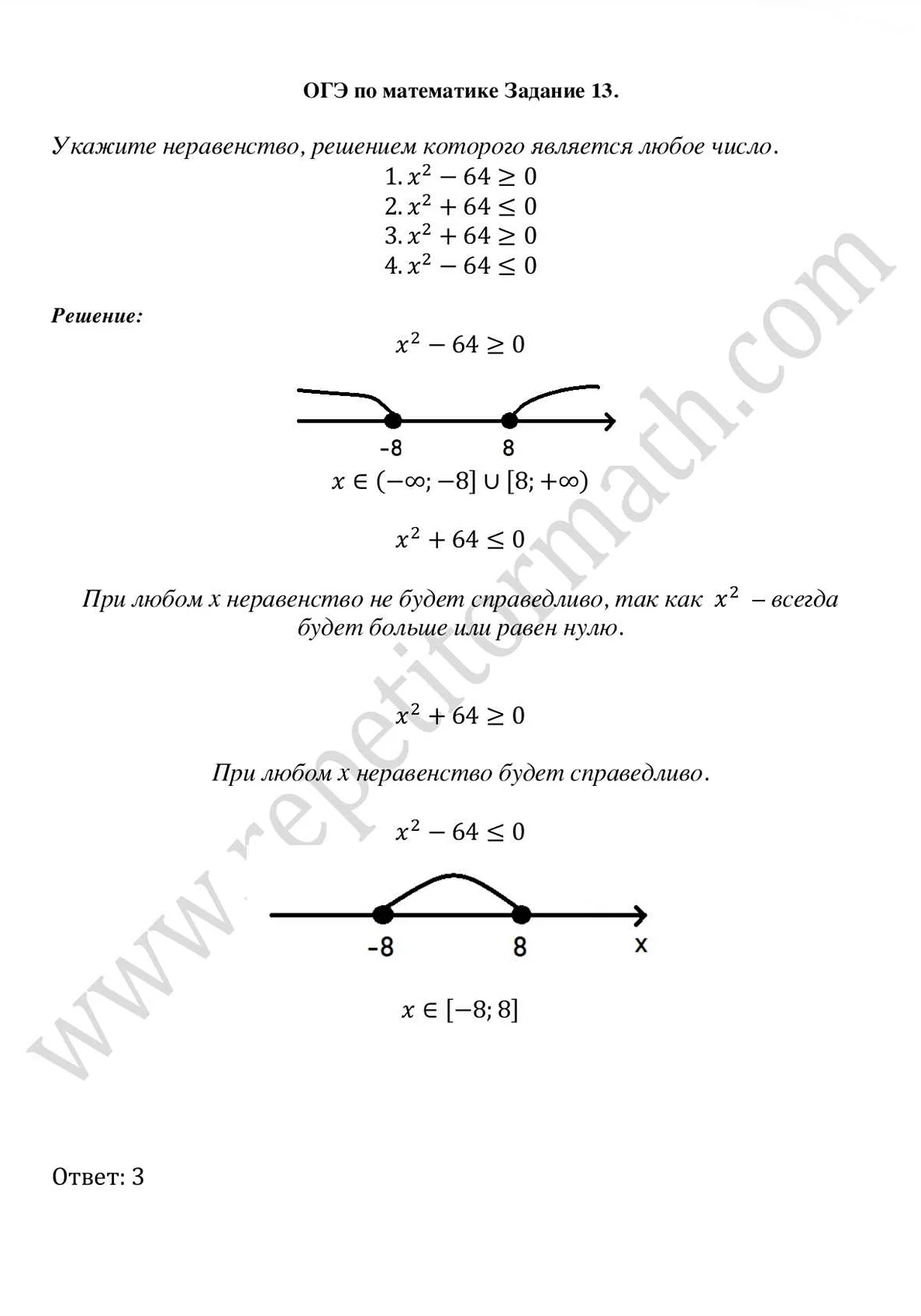
Отражение функции x2 относительно оси OX происходит следующим образом: все точки графика, которые находятся выше оси OX, переносятся вниз относительно этой оси, а все точки, которые находятся ниже оси OX, переносятся вверх относительно нее. Таким образом, получается новый график, симметричный исходному относительно оси OX.

Отражение функции x2 относительно оси OY происходит аналогичным образом: все точки графика, которые находятся справа от оси OY, переносятся влево относительно этой оси, а все точки, которые находятся слева от оси OY, переносятся вправо относительно нее. Получается новый график, симметричный исходному относительно оси OY.

Для наглядности, рассмотрим график функции y = x2 и его отражения относительно осей OX и OY:

1. Отражение относительно оси OX:

График функции y = x2

Отражение графика относительно оси OX

2. Отражение относительно оси OY:

График функции y = x2

Отражение графика относительно оси OY

Отражение функции x2 на графиках и графах позволяет увидеть симметрию точек относительно осей и исследовать особенности графика функции.

Решение уравнений

Примеры уравнений:

1. 2x + 5 = 13
2. x^2 — 4 = 0
3. 3(x + 2) = 15

Для решения уравнений используются различные методы, включая алгебраические и графические методы. Один из основных методов — метод подстановки, при котором значение неизвестной находится путем последовательной подстановки значений и проверки равенства левой и правой частей уравнения.

Другим методом решения уравнений является метод факторизации, который основывается на разложении выражения на множители и приравнивании каждого множителя к нулю.

Иногда для решения уравнений используются специальные формулы, такие как формула дискриминанта для квадратных уравнений или формула корней кубического уравнения.