От чего зависит колебания математического маятника
Содержимое
- 1 От чего зависит колебания математического маятника
- 1.1 Колебания математического маятника: факторы и зависимости
- 1.2 Видео по теме:
- 1.3 Математический маятник и его устройство
- 1.4 Влияние длины подвеса на колебания маятника
- 1.5 Зависимость периода колебаний от массы груза
- 1.6 Взаимосвязь амплитуды и длины маятника
- 1.7 Влияние трения на колебания математического маятника
- 1.8 Роль начальной скорости в колебаниях маятника
- 1.9 Эффект гравитации на колебания математического маятника
- 1.10 Влияние внешних сил на колебания маятника
- 1.11 Вопрос-ответ:
- 1.11.0.1 Какие факторы влияют на колебания математического маятника?
- 1.11.0.2 Как зависит период колебаний математического маятника от его длины?
- 1.11.0.3 Как влияет масса груза на колебания математического маятника?
- 1.11.0.4 Как сила сопротивления воздуха влияет на колебания математического маятника?
- 1.11.0.5 Как сила трения в подвесе маятника влияет на его колебания?
- 1.11.0.6 Какие факторы влияют на колебания математического маятника?
- 1.11.0.7 Как связаны длина математического маятника и его период колебаний?
Подробное объяснение факторов, влияющих на колебания математического маятника: длина подвеса, масса груза, амплитуда колебаний, а также сила сопротивления и присутствие внешних сил.
Математический маятник — это устройство, состоящее из невесомой нити и точечной массы, которая может свободно колебаться в вертикальной плоскости под действием сил тяжести. Изучение его колебаний имеет большое значение для многих областей науки и техники, таких как физика, инженерия и астрономия.
Основные факторы, влияющие на колебания математического маятника, — это его длина и ускорение свободного падения. Длина нити определяет период колебаний: чем длиннее нить, тем больше времени требуется для одного полного колебания. Ускорение свободного падения также влияет на период колебаний: чем больше ускорение, тем быстрее маятник будет колебаться.
Другим важным фактором, влияющим на колебания математического маятника, является амплитуда колебаний — максимальное отклонение маятника от положения равновесия. Чем больше амплитуда колебаний, тем больше энергии требуется для поддержания движения маятника.
Колебания математического маятника также зависят от его массы и начальных условий. Чем больше масса маятника, тем больше энергии требуется для его колебаний. Начальные условия, такие как начальное отклонение и начальная скорость, также влияют на колебания — они определяют начальную фазу и амплитуду колебаний.
Изучение зависимостей между различными факторами и свойствами колебаний математического маятника является важной задачей для понимания и применения законов механики. Эти зависимости позволяют улучшать проектирование и контроль систем, использующих математические маятники, а также изучать колебания в природе, такие как колебания атмосферы и планет.
Колебания математического маятника: факторы и зависимости

Математический маятник представляет собой систему, в которой тело подвешено на нерастяжимой нити и может свободно двигаться в горизонтальной плоскости. Колебания маятника возникают из-за взаимодействия силы тяжести и силы натяжения нити.
Факторы, влияющие на колебания математического маятника, включают длину нити, массу тела, амплитуду начального отклонения и силу трения. Длина нити является основным фактором, определяющим период колебаний маятника. Чем длиннее нить, тем медленнее колебания.
Масса тела также оказывает влияние на колебания маятника. Чем больше масса, тем медленнее будут колебания. Амплитуда начального отклонения определяет дальность движения маятника. Чем больше амплитуда, тем дальше будет двигаться маятник.
Сила трения оказывает существенное влияние на колебания математического маятника. Она может привести к затуханию колебаний и уменьшению их амплитуды. Чтобы уменьшить влияние силы трения, можно использовать специальные механизмы или выбирать материалы с меньшим коэффициентом трения.
Зависимости между факторами и колебаниями математического маятника могут быть описаны с помощью математических формул и уравнений. На основе этих зависимостей можно проводить различные эксперименты и исследования, чтобы лучше понять физические законы, управляющие колебаниями маятника.
Видео по теме:
Математический маятник и его устройство
Устройство математического маятника включает в себя несколько основных элементов:
| 1 | Груз | — это точечная масса, которая служит основой для колебаний математического маятника. Его масса и форма могут варьироваться в зависимости от конструкции маятника. |
| 2 | Нить или стержень | — это элемент, на котором груз подвешен. Нить обычно представляет собой гибкую невесомую веревку, а стержень — жесткий невесомый предмет. |
| 3 | Точка подвеса | — это место, где нить или стержень прикрепляются к некоторой опоре. Эта точка обеспечивает свободное вращение маятника вокруг нее. |
Математический маятник можно использовать для изучения колебательных процессов и исследования различных зависимостей, таких как зависимость периода колебаний от длины нити или от ускорения свободного падения. Он также является важным инструментом для изучения основных законов механики и теории колебаний.
Влияние длины подвеса на колебания маятника

Математический маятник – это идеализированная система, состоящая из точечной массы, закрепленной на невесомой нерастяжимой нити или стержне. Длина подвеса маятника представляет собой расстояние от точки подвеса до центра масс маятника.
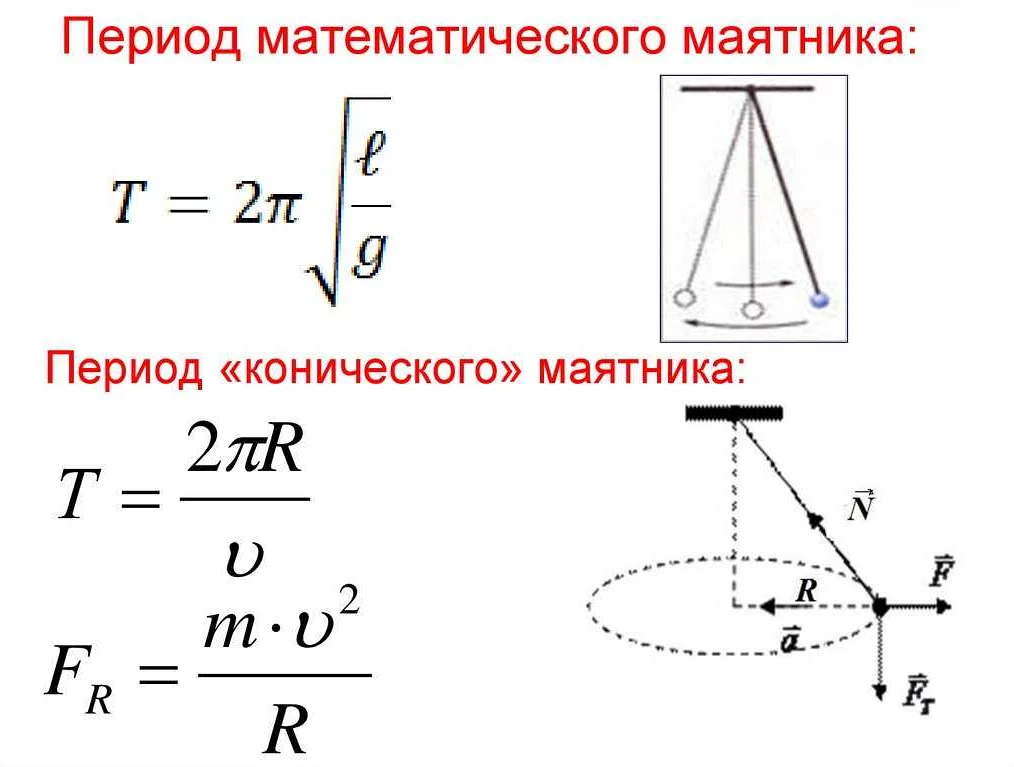
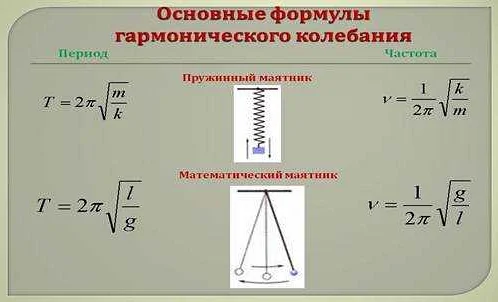
Зависимость между длиной подвеса и периодом колебаний маятника описывается формулой:
Формула для расчета периода колебаний маятника:
| T = 2π√(l/g) |
Где:
- T — период колебаний маятника;
- π — математическая константа, приближенно равная 3,14;
- l — длина подвеса;
- g — ускорение свободного падения, приближенно равное 9,8 м/с².
Из этой формулы видно, что период колебаний маятника обратно пропорционален квадратному корню из длины подвеса. То есть, при увеличении длины подвеса период колебаний увеличивается, а при уменьшении длины подвеса период колебаний уменьшается.
Чем длиннее подвес математического маятника, тем медленнее он будет колебаться. Длина подвеса также влияет на частоту колебаний маятника – количество колебаний в единицу времени. Чем длиннее подвес, тем меньше частота колебаний маятника.
Таким образом, длина подвеса является важным параметром, определяющим характеристики колебаний математического маятника. При изучении маятника необходимо учитывать длину его подвеса и ее влияние на период и частоту колебаний.
Зависимость периода колебаний от массы груза

Период колебаний математического маятника зависит от многих факторов, включая массу груза, длину подвеса и силу гравитации. В данном разделе рассмотрим, как масса груза влияет на период колебаний.
Масса груза является одним из основных параметров математического маятника, который влияет на его поведение. Чем больше масса груза, тем медленнее будет происходить колебание маятника, и наоборот, чем меньше масса груза, тем быстрее будут происходить колебания.
Для демонстрации зависимости периода колебаний от массы груза, можно провести эксперимент, меняя массу груза и фиксируя время одного полного колебания маятника. Результаты эксперимента можно представить в виде таблицы.
Масса груза (кг)Период колебания (сек)
| 0.1 | 1.2 |
| 0.2 | 1.4 |
| 0.3 | 1.6 |
| 0.4 | 1.8 |
| 0.5 | 2.0 |
Из представленной таблицы видно, что с увеличением массы груза период колебания также увеличивается. Это свидетельствует о прямой зависимости между массой груза и периодом колебаний.
В заключение, можно сказать, что масса груза является важным фактором, определяющим период колебаний математического маятника. Чем больше масса груза, тем медленнее будет происходить колебание маятника, и наоборот, чем меньше масса груза, тем быстрее будут происходить колебания.
Взаимосвязь амплитуды и длины маятника

Амплитуда колебаний математического маятника зависит от его длины. Чем длиннее маятник, тем меньше его амплитуда.
Это связано с законом сохранения энергии. В начальный момент колебаний маятник находится в верхней точке своей траектории, где его потенциальная энергия максимальна, а кинетическая энергия равна нулю. По мере спуска маятника вниз, потенциальная энергия уменьшается, а кинетическая энергия увеличивается. В нижней точке траектории маятник достигает максимальной кинетической энергии и минимальной потенциальной энергии.
По мере возвращения маятника обратно в верхнюю точку траектории, кинетическая энергия уменьшается, а потенциальная энергия увеличивается. Верхняя точка достигается, когда кинетическая энергия равна нулю, а потенциальная энергия снова максимальна.
Закон сохранения энергии говорит о том, что потенциальная и кинетическая энергии в системе остаются постоянными. Из этого следует, что сумма потенциальной энергии и кинетической энергии маятника в любой точке траектории также остается постоянной.
При увеличении длины маятника, его потенциальная энергия будет увеличиваться, а кинетическая энергия будет уменьшаться. Это приводит к уменьшению амплитуды колебаний маятника.
Таким образом, длина математического маятника является фактором, влияющим на его амплитуду. Чем длиннее маятник, тем меньше его амплитуда колебаний.
Влияние трения на колебания математического маятника

Одним из основных эффектов трения на колебания математического маятника является постепенное затухание амплитуды колебаний. При наличии трения энергия, передаваемая колеблющемуся маятнику, постепенно превращается в тепловую энергию, что приводит к уменьшению амплитуды колебаний с течением времени. Таким образом, трение может сказываться на стабильности и длительности колебаний математического маятника.
Однако, не всегда трение негативно влияет на колебания маятника. В некоторых случаях трение может сыграть положительную роль, помогая стабилизировать колебания и предотвращать слишком сильные и хаотические колебания. Это особенно актуально для маятников с большой амплитудой или маятников со сложной конструкцией.
Для учета влияния трения на колебания математического маятника необходимо учитывать его коэффициент трения, который зависит от типа трения и поверхностей, соприкасающихся между собой. Коэффициент трения может быть определен экспериментально или с помощью теоретических расчетов. Зная коэффициент трения, можно предсказать влияние трения на колебания маятника и принять необходимые меры для его минимизации или использования в своих целях.
Таким образом, трение является важным фактором, влияющим на колебания математического маятника. Оно может затухать амплитуду колебаний и стабилизировать их, а также изменять их характеристики в зависимости от коэффициента трения. Исследование и учет трения позволяют более точно предсказывать и контролировать колебания математического маятника в различных условиях.
Роль начальной скорости в колебаниях маятника
Начальная скорость играет важную роль в колебаниях математического маятника. Она влияет на период и амплитуду колебаний, а также на форму графика зависимости угла от времени.
Период колебаний – это время, за которое маятник совершает одно полное колебание, то есть проходит от одной крайней точки до другой и обратно. Начальная скорость влияет на период колебаний: чем больше начальная скорость, тем больше период.
Амплитуда колебаний – это максимальное отклонение маятника от положения равновесия. Начальная скорость также влияет на амплитуду колебаний: чем больше начальная скорость, тем больше амплитуда.
График зависимости угла от времени может иметь различные формы в зависимости от начальной скорости. Например, при нулевой начальной скорости маятник совершает колебания вокруг положения равновесия, а при ненулевой начальной скорости маятник может совершать колебания с постепенным затуханием или с возрастающей амплитудой.
Эффект гравитации на колебания математического маятника
Эффект гравитации на колебания математического маятника заключается в том, что сила тяжести, действующая на точечную массу, определяет его равновесное положение и влияет на величину периода и частоты колебаний. Чем больше масса точечного тела, тем сильнее действует гравитация, и тем больше период колебаний. Также величина силы тяжести зависит от высоты подвеса маятника: чем выше точка подвеса, тем меньше сила гравитации, и, соответственно, больше период колебаний.
Интересно отметить, что колебания математического маятника вообще не зависят от массы точечного тела. Это связано с тем, что на маятник действуют силы, которые не зависят от массы точечного тела, а только от его положения. Это позволяет использовать математические маятники для измерения времени и создания точных часов.
Влияние внешних сил на колебания маятника
Колебания математического маятника могут быть подвержены влиянию различных внешних сил, которые могут изменять его период, амплитуду и фазу. Эти внешние силы могут возникать из разных источников и иметь разную природу.
Одним из основных факторов, влияющих на колебания маятника, является сила трения. Трение может приводить к затуханию колебаний и уменьшению их амплитуды. Чем больше трения, тем быстрее затухают колебания. Для учета влияния трения на колебания маятника используются специальные математические модели.
Другой важной внешней силой, влияющей на колебания маятника, является сила сопротивления воздуха. При движении маятника в воздухе сила сопротивления воздуха противодействует его движению, что приводит к уменьшению амплитуды колебаний и изменению периода маятника. Чтобы учесть влияние сопротивления воздуха, необходимо учитывать его значение при решении уравнений движения маятника.
Кроме того, на колебания маятника могут оказывать влияние другие внешние силы, такие как упругая сила, сила гравитации, сила магнитного поля и др. Все эти силы могут изменять характеристики колебаний маятника и требуют учета при анализе и решении задач по маятникам.
Итак, внешние силы играют важную роль в определении характеристик колебаний математического маятника. Их влияние может быть различным и зависит от природы и интенсивности каждой конкретной силы. Для точного анализа колебаний маятника необходимо учитывать все внешние силы и их влияние на его движение.
Вопрос-ответ:
Какие факторы влияют на колебания математического маятника?
На колебания математического маятника влияют несколько факторов. Во-первых, длина маятника — чем длиннее маятник, тем медленнее будут его колебания. Во-вторых, масса груза, который закреплен на конце маятника — чем больше масса груза, тем медленнее будут его колебания. Также на колебания маятника может влиять сила сопротивления воздуха и сила трения в подвесе маятника.
Как зависит период колебаний математического маятника от его длины?
Период колебаний математического маятника зависит от его длины. Формула зависимости периода от длины маятника выглядит следующим образом: период равен 2 * пи * корень из длины маятника, поделенной на ускорение свободного падения. Таким образом, период колебаний увеличивается с увеличением длины маятника.
Как влияет масса груза на колебания математического маятника?
Масса груза, который закреплен на конце математического маятника, также влияет на его колебания. Чем больше масса груза, тем медленнее будут колебания маятника. Это связано с тем, что большая масса создает большую инерцию, и маятник будет тратить больше времени на прохождение каждого колебания.
Как сила сопротивления воздуха влияет на колебания математического маятника?
Сила сопротивления воздуха может замедлить колебания математического маятника. При наличии сопротивления воздуха энергия маятника постепенно теряется, и колебания становятся менее амплитудными. Однако, если сила сопротивления воздуха незначительна, то ее влияние на колебания маятника может быть незаметным.
Как сила трения в подвесе маятника влияет на его колебания?
Сила трения в подвесе математического маятника также может влиять на его колебания. Если трение в подвесе мало, то колебания маятника будут практически без затухания. Однако, если трение в подвесе сильно, то колебания маятника будут затухать быстро, и маятник перестанет колебаться через некоторое время.
Какие факторы влияют на колебания математического маятника?
На колебания математического маятника влияют несколько факторов. Основными из них являются длина маятника, ускорение свободного падения, и начальный угол отклонения. Длина маятника определяет период колебаний, чем длиннее маятник, тем больше времени требуется на один полный цикл. Ускорение свободного падения тоже влияет на период колебаний, так как сила тяжести зависит от него. Начальный угол отклонения также оказывает влияние на колебания — чем больше отклонение, тем больше будет амплитуда колебаний.
Как связаны длина математического маятника и его период колебаний?
Длина математического маятника прямо влияет на его период колебаний. Формула для вычисления периода колебаний математического маятника — T = 2 * π * √(L/g), где T — период колебаний, L — длина маятника, g — ускорение свободного падения. Из этой формулы видно, что период колебаний математического маятника увеличивается с увеличением длины маятника. Это означает, что чем длиннее маятник, тем дольше будет время, требующееся для совершения одного полного колебания.

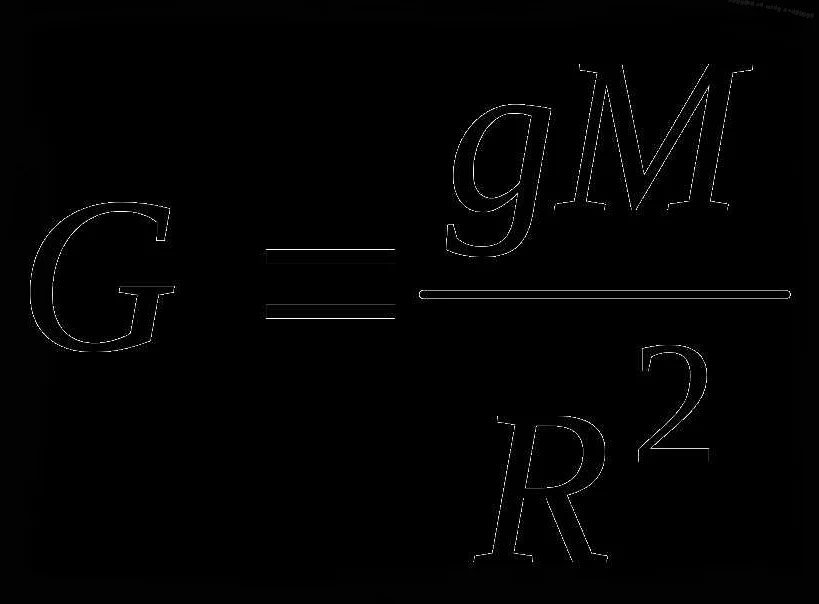


Статья очень интересна и познавательна! Я всегда задавалась вопросом, что влияет на колебания математического маятника. Оказывается, есть множество факторов, которые влияют на этот процесс. Например, длина маятника играет важную роль: чем длиннее маятник, тем больше времени занимают его колебания. Также влияет масса груза на конце маятника: чем больше масса, тем медленнее колебания. Интересно, что на колебания также влияет сила трения воздуха: она замедляет движение маятника. Кроме того, влиять на колебания может и начальный угол отклонения: чем больше угол, тем сильнее колебания. Все эти зависимости и факторы делают изучение математического маятника увлекательным и позволяют более глубоко понять законы физики. Спасибо за такую информативную статью!
Спасибо за интересную статью! Я всегда был увлечен физикой и математикой, поэтому тема колебаний математического маятника вызывает у меня особый интерес. В статье были очень хорошо объяснены основные факторы, влияющие на колебания маятника. Я уже знал, что длина нити и ускорение свободного падения существенно влияют на период колебаний, но мне было интересно узнать о других факторах. Особенно мне понравилось, как были объяснены зависимости между факторами. Например, то, что увеличение длины нити приводит к увеличению периода колебаний, меня очень заинтересовало. Также было интересно узнать, что масса маятника не влияет на период колебаний, а влияет только на амплитуду, что является очень важным фактом. Статья помогла мне лучше понять физические законы, лежащие в основе колебаний математического маятника, и расширила мои знания в этой области. Теперь я смогу лучше понять и объяснить принципы работы маятников в различных устройствах и механизмах. Хотелось бы отметить, что статья написана очень доступным языком, и ее было легко читать и понимать. Очень рад, что наткнулся на эту статью, и надеюсь увидеть еще больше подобных материалов на вашем сайте. Спасибо за вашу работу!