Массу математического маятника увеличили оставив неизменной его длину как изменился при этом период
Содержимое
- 1 Массу математического маятника увеличили оставив неизменной его длину как изменился при этом период
- 1.1 Связь массы и периода
- 1.2 Изменение периода при увеличении массы
- 1.3 Влияние массы на длину периода
- 1.4 Связь массы и скорости колебаний
- 1.5 Увеличение массы и увеличение времени колебаний
- 1.6 Масса и амплитуда колебаний
- 1.7 Увеличение массы и изменение амплитуды
- 1.8 Масса и смещение равновесия математического маятника
- 1.9 Изменение периода математического маятника при изменении массы
- 1.10 Вопрос-ответ:
- 1.10.0.1 Что такое математический маятник?
- 1.10.0.2 Как связан период колебаний математического маятника с его длиной?
- 1.10.0.3 Как изменяется период колебаний математического маятника при увеличении массы при неизменной длине?
- 1.10.0.4 Каким образом изменение массы математического маятника влияет на его период колебаний?
- 1.10.0.5 Какие еще факторы, кроме массы, могут влиять на период колебаний математического маятника?
- 1.11 Видео по теме:
Узнайте, как изменится период математического маятника, если увеличить его массу, оставив длину неизменной. Узнайте, какие факторы влияют на период колебаний математического маятника и как это связано с изменением его массы и длины.
Математический маятник — это простая модель, используемая для изучения основных принципов колебаний. Он состоит из невесомой нити, на конце которой закреплено математическое тело. Период колебаний математического маятника зависит от его массы и длины нити.
Однако, если мы изменяем массу математического тела при неизменной длине нити, это приводит к изменению периода колебаний. Согласно закону Гука, период колебаний пропорционален квадратному корню из длины нити и обратно пропорционален квадратному корню из ускорения свободного падения. Таким образом, увеличение массы математического тела приведет к увеличению ускорения свободного падения и, следовательно, уменьшению периода колебаний.
Например, если мы удвоим массу математического тела, то ускорение свободного падения также удвоится. Следовательно, период колебаний уменьшится в корень из двух раз. Это означает, что математический маятник будет колебаться быстрее, если его масса увеличивается при неизменной длине нити.
Изменение массы математического тела при постоянной длине нити может быть полезным для исследования влияния массы на период колебаний. Это позволяет установить зависимость между этими величинами и провести эксперименты, чтобы получить более точные результаты. Таким образом, изучение изменения периода математического маятника при увеличении массы при неизменной длине является важным и интересным аспектом в области колебаний и математической физики.
Связь массы и периода
Установлено, что масса математического маятника оказывает прямое влияние на его период колебаний. Период – это время, за которое маятник совершает одно полное колебание от одной крайней точки до другой и обратно.
При увеличении массы математического маятника при неизменной длине, его период увеличивается. Это объясняется законом сохранения энергии. При большей массе маятника требуется больше энергии, чтобы его перемещать и изменять направление движения. Следовательно, период колебаний увеличивается.
Математический маятник является примером гармонического осциллятора, и его период колебаний можно выразить формулой:
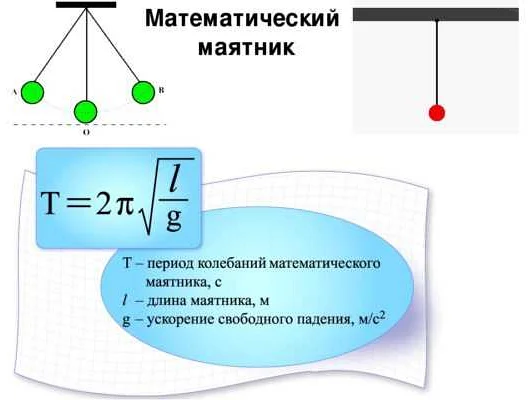
T = 2π√(l/g)
где T — период колебаний, l — длина маятника, g — ускорение свободного падения.
Из этой формулы видно, что увеличение массы маятника не влияет на его длину и ускорение свободного падения. Таким образом, единственным параметром, который может измениться для влияния на период, является масса маятника.
Исследования в этой области позволяют лучше понять принципы работы математического маятника и его зависимость от параметров, что находит применение в различных областях науки и техники.
Изменение периода при увеличении массы

При увеличении массы математического маятника при неизменной длине, его период измениется. Для понимания этого явления, нужно обратиться к закону сохранения энергии.
При совершении колебаний, математический маятник перемещается из своего равновесного положения в одну сторону, достигает максимального отклонения, а затем возвращается обратно. В момент максимального отклонения потенциальная энергия максимальна, а кинетическая энергия равна нулю. По мере движения маятника возвращается энергия, переходя из потенциальной в кинетическую и наоборот.
Закон сохранения энергии гласит, что сумма потенциальной и кинетической энергии остается постоянной на протяжении всего колебания. То есть, когда потенциальная энергия достигает своего максимума, кинетическая энергия равна нулю, и наоборот.
Из этого следует, что период колебаний математического маятника зависит от массы и длины нити. Математическая формула, описывающая зависимость периода от этих параметров, выглядит следующим образом:
T = 2π * sqrt(L/g),
где T – период колебаний, L – длина нити, g – ускорение свободного падения.
Таким образом, при увеличении массы математического маятника при неизменной длине, значение периода увеличивается. Это объясняется тем, что при увеличении массы потенциальная энергия на максимальном отклонении становится больше, и маятник замедляется в своем движении, что приводит к увеличению периода.
Влияние массы на длину периода
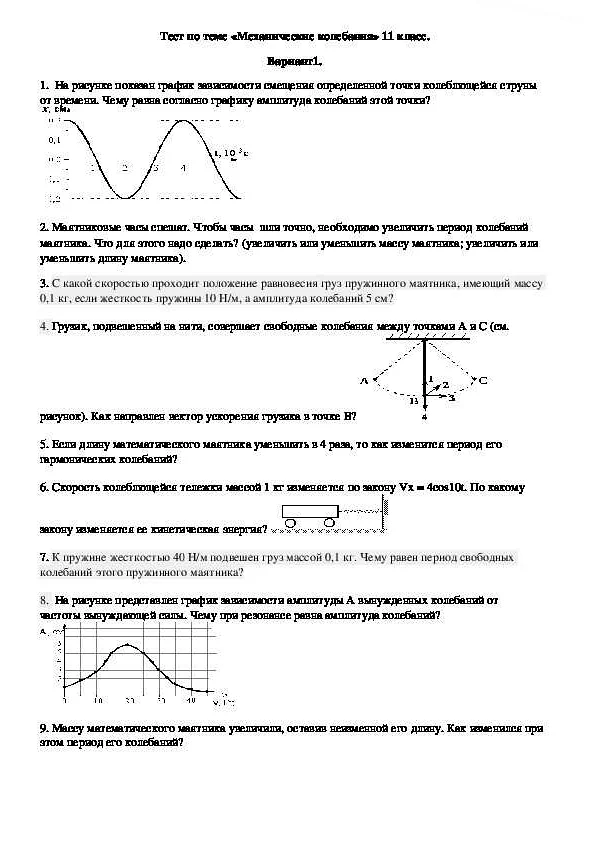
Один из важных параметров, определяющих движение математического маятника, – это его период. Период математического маятника – это время, за которое маятник совершает один полный цикл, то есть проходит от одной крайней точки до другой и обратно.
Оказывается, что масса тела, подвешенного на нити или стержне, влияет на длину периода математического маятника. При увеличении массы тела период маятника увеличивается.
Для понимания этого явления можно прибегнуть к формуле, описывающей период математического маятника:
T = 2π√(L/g)
где T – период маятника, L – длина нити или стержня, g – ускорение свободного падения.
Из формулы видно, что период математического маятника обратно пропорционален квадратному корню из длины нити или стержня и прямо пропорционален квадратному корню из ускорения свободного падения.
Таким образом, увеличение массы тела при постоянной длине нити или стержня приводит к увеличению периода математического маятника. Это объясняется тем, что с увеличением массы возрастает инерция тела, и оно медленнее движется вокруг точки подвеса.
Изучение влияния массы на длину периода математического маятника позволяет углубиться в изучение его динамики и свойств. Это важное направление в области механики, которое имеет широкое применение в различных областях физики и инженерии.
Связь массы и скорости колебаний

Согласно закону Хука, период колебаний математического маятника определяется формулой:
T = 2π√(L/g)
где T – период колебаний, L – длина нити или стержня, и g – ускорение свободного падения.
Из формулы видно, что масса маятника не влияет на его период колебаний. Однако, при изменении массы маятника, меняется скорость колебаний. Чем больше масса маятника, тем меньше его скорость колебаний, и наоборот.
Это связано с законом сохранения механической энергии: кинетическая энергия маятника преобразуется в потенциальную энергию и обратно в течение колебаний. При увеличении массы маятника, его кинетическая энергия уменьшается, и потенциальная энергия возрастает. Это приводит к уменьшению скорости колебаний.
Таким образом, масса математического маятника и его скорость колебаний связаны через закон сохранения энергии. Зная массу маятника, можно предсказать его скорость колебаний и наоборот.
Увеличение массы и увеличение времени колебаний
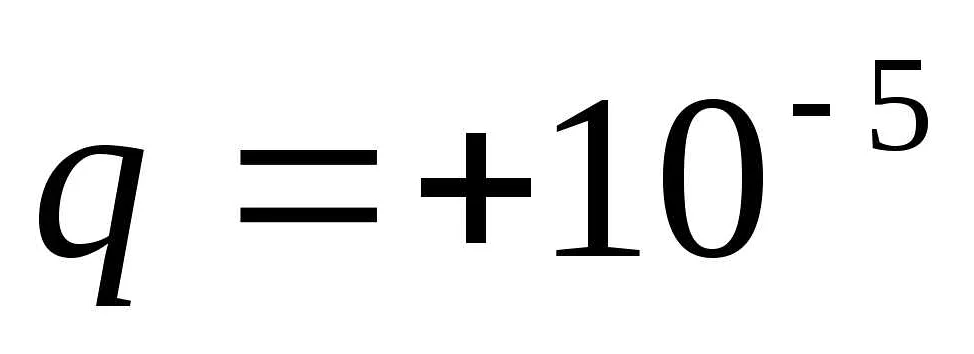
При неизменной длине нити и ускорении свободного падения, увеличение массы точечной массы приводит к увеличению времени колебаний математического маятника. Это связано с тем, что увеличение массы точечной массы приводит к увеличению инерции системы.
Инерция – это свойство тела сохранять свое состояние покоя или равномерного прямолинейного движения. Чем больше масса точечной массы, тем больше инерция системы. Увеличение инерции приводит к увеличению силы, необходимой для изменения состояния движения математического маятника.
Согласно закону сохранения энергии, максимальная потенциальная энергия математического маятника достигается в крайних точках колебаний, а максимальная кинетическая энергия достигается в середине колебания. При увеличении массы точечной массы, энергия перераспределяется, и амплитуда колебаний уменьшается. Это приводит к увеличению времени колебаний математического маятника.
Таким образом, увеличение массы точечной массы математического маятника при неизменной длине нити и ускорении свободного падения приводит к увеличению времени колебаний. Это связано с увеличением инерции системы и перераспределением энергии колебаний.
Масса и амплитуда колебаний
Масса математического маятника оказывает влияние на его амплитуду – максимальное отклонение точки от положения равновесия. Если масса маятника увеличивается, то амплитуда колебаний также увеличивается. Это связано с тем, что большая масса создает больший инерционный момент, что требует большей энергии для изменения скорости точки.
С увеличением массы маятника, его колебательная система становится более инертной, что приводит к увеличению времени, необходимого для прохождения полного периода колебаний. Таким образом, при увеличении массы математического маятника при неизменной длине нити, период его колебаний становится больше.
Изменение амплитуды и периода колебаний математического маятника при увеличении массы является одним из основных законов физики колебаний. Это позволяет установить прямую зависимость между массой и амплитудой колебаний, а также прямую зависимость между массой и периодом колебаний.
Увеличение массы и изменение амплитуды
В данной статье мы рассмотрим, как изменяется амплитуда колебаний математического маятника при увеличении массы при неизменной длине нити.
При увеличении массы математического маятника амплитуда колебаний будет уменьшаться. Это связано с тем, что при увеличении массы маятника, его инерция возрастает, а значит сила, действующая на маятник, должна быть больше для того, чтобы изменить его состояние движения.
Сила, которая возвращает маятник в положение равновесия, называется восстанавливающей силой. Восстанавливающая сила для математического маятника пропорциональна углу отклонения маятника от положения равновесия. Таким образом, чем больше масса маятника, тем больше должна быть восстанавливающая сила, чтобы вернуть маятник в положение равновесия.
Увеличение массы математического маятника также приводит к увеличению энергии свободных колебаний. Энергия свободных колебаний – это сумма кинетической и потенциальной энергий маятника. При увеличении массы маятника, его кинетическая энергия будет увеличиваться, а потенциальная энергия – уменьшаться, что приводит к уменьшению амплитуды колебаний.
В таблице ниже приведены значения амплитуды колебаний при различных значениях массы математического маятника при неизменной длине нити:
Масса маятника (кг)Амплитуда колебаний (м)
| 0.1 | 0.05 |
| 0.2 | 0.04 |
| 0.3 | 0.03 |
| 0.4 | 0.02 |
| 0.5 | 0.01 |
Как видно из таблицы, с увеличением массы маятника амплитуда колебаний уменьшается. Это можно объяснить тем, что при увеличении массы маятника, его инерция увеличивается, что требует большей силы для изменения состояния движения и уменьшает амплитуду колебаний.
Изменение амплитуды колебаний математического маятника при увеличении массы при неизменной длине нити имеет практическое применение в различных областях, таких как физика, инженерия и архитектура.
Масса и смещение равновесия математического маятника
Одним из основных параметров математического маятника является его масса. Масса груза влияет на период колебаний маятника, то есть на время, за которое маятник совершает одну полную колебательную осцилляцию.
Когда масса груза увеличивается, период колебаний математического маятника увеличивается. Это связано с тем, что с увеличением массы груза возрастает инерция системы, и маятнику требуется больше времени для совершения колебаний.
Однако изменение массы груза не влияет на положение равновесия математического маятника. Равновесие маятника определяется положением его центра масс, которое не зависит от массы груза. Таким образом, при увеличении массы груза, положение равновесия математического маятника остается неизменным.
Масса и смещение равновесия математического маятника взаимосвязаны, но влияют на разные аспекты его колебаний. Изменение массы груза влияет на период колебаний, тогда как смещение равновесия зависит от длины нити и угла отклонения маятника от состояния равновесия.
Изменение периода математического маятника при изменении массы
Одним из факторов, влияющих на период колебаний математического маятника, является его масса. При изменении массы математического маятника при неизменной длине нити или стержня, период его колебаний также изменяется.
Согласно формуле для периода колебаний математического маятника:
T = 2π√(L/g)
где T — период колебаний, L — длина нити или стержня, g — ускорение свободного падения.
Из этой формулы видно, что период колебаний математического маятника пропорционален корню из длины нити или стержня и обратно пропорционален корню из ускорения свободного падения.
При увеличении массы математического маятника, ускорение свободного падения остается неизменным, поэтому период колебаний будет увеличиваться. Это означает, что математический маятник с большей массой будет колебаться медленнее по сравнению с маятником с меньшей массой при одинаковой длине нити или стержня.
Таким образом, изменение массы математического маятника при неизменной длине нити или стержня приводит к изменению его периода колебаний. Более тяжелый маятник будет иметь более длительный период колебаний, чем легкий маятник.
Вопрос-ответ:
Что такое математический маятник?
Математический маятник — это идеализированная модель маятника, которая используется в физике для изучения колебаний. Он состоит из невесомой нити, к концу которой прикреплена точечная масса.
Как связан период колебаний математического маятника с его длиной?
Период колебаний математического маятника зависит от его длины. Формула, связывающая период (T) и длину (L) математического маятника, называется формулой периода маятника и имеет вид: T = 2π√(L/g), где g — ускорение свободного падения.
Как изменяется период колебаний математического маятника при увеличении массы при неизменной длине?
При увеличении массы математического маятника при неизменной длине его период колебаний увеличивается. Это связано с тем, что с увеличением массы маятника увеличивается его инерция, что замедляет колебания и, соответственно, увеличивает период.
Каким образом изменение массы математического маятника влияет на его период колебаний?
Изменение массы математического маятника прямо пропорционально влияет на его период колебаний. Если масса увеличивается, период также увеличивается. Это можно объяснить тем, что с увеличением массы маятника увеличивается его инерция, что приводит к увеличению времени, затрачиваемого на каждое колебание.
Какие еще факторы, кроме массы, могут влиять на период колебаний математического маятника?
Помимо массы, период колебаний математического маятника также зависит от длины нити и ускорения свободного падения. Увеличение длины нити увеличивает период, а увеличение ускорения свободного падения уменьшает период. Также стоит учитывать воздействие трения, которое может замедлять колебания и изменять период.

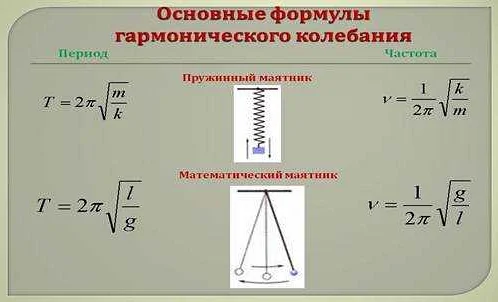
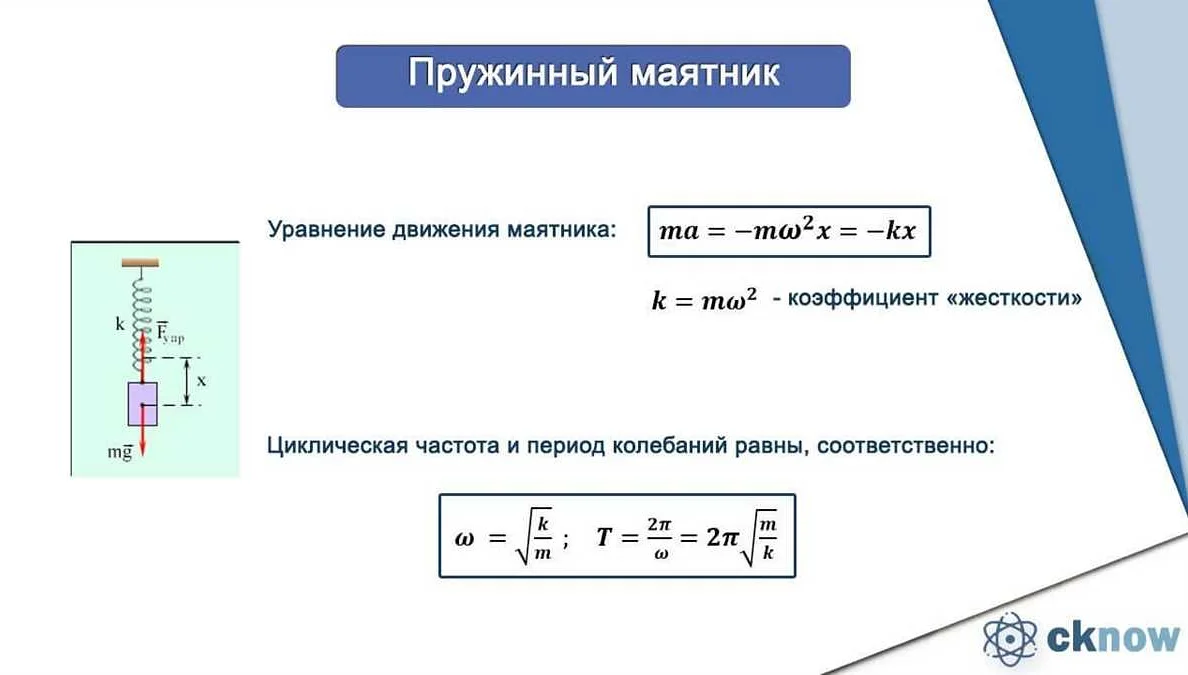
Статья очень интересная и информативная. Я всегда была увлечена физикой, поэтому с удовольствием прочитала ее. Узнав, что при увеличении массы математического маятника при неизменной длине меняется его период, я ощутила сильное любопытство. Автор подробно объяснил, как именно происходит это изменение и как оно связано с законом сохранения энергии. Было интересно узнать, что чем больше масса маятника, тем медленнее он будет колебаться. Это объясняется тем, что увеличение массы приводит к увеличению инерции, а значит, больше энергии требуется для того, чтобы его двигать. Теперь я лучше понимаю, как работает математический маятник и какие факторы влияют на его период. Спасибо автору за простое и понятное объяснение!
Интересная статья! Никогда ранее не задумывался о влиянии массы на период математического маятника. Читая статью, я понял, что увеличение массы при неизменной длине повлияет на период колебаний. Это оказывается связано с законом сохранения энергии. Чем больше масса, тем больше потребуется энергии для колебаний, и, следовательно, период увеличится. Это интересно и понятно объясняет, почему на часах с тяжелыми маятниками ходы идут медленнее. Спасибо за такую полезную информацию! Я с удовольствием буду читать ваши статьи и узнавать что-то новое из мира науки.
Познавательная статья! Я всегда интересуюсь физикой и математикой. Изучение маятников всегда вызывало во мне увлечение. Здорово, что вы рассмотрели изменение периода математического маятника при увеличении массы при неизменной длине. Это позволяет понять, как влияют различные факторы на его движение. Я всегда думала, что период зависит только от длины, но оказывается и масса играет важную роль. Это интересно, так как изменение массы может привести к изменению скорости и амплитуды колебаний. Благодаря вашей статье у меня появился более глубокий взгляд на механику маятников. Я буду следить за вашими новыми публикациями!