От чего зависит период колебаний математического маятника
Содержимое
- 1 От чего зависит период колебаний математического маятника
- 1.1 Влияние массы на период колебаний математического маятника
- 1.2 Масса груза, определяющая период колебаний
- 1.3 Влияние длины нити на период колебаний математического маятника
- 1.4 Длина нити, влияющая на время осцилляций
- 1.5 Влияние силы трения на период колебаний математического маятника
- 1.6 Сила трения, влияющая на время осцилляций
- 1.7 Влияние ускорения свободного падения на период колебаний математического маятника
- 1.8 Ускорение свободного падения, определяющее период колебаний
- 1.9 Влияние амплитуды колебаний на период математического маятника
- 1.10 Вопрос-ответ:
- 1.10.0.1 Что такое математический маятник?
- 1.10.0.2 Каковы факторы, влияющие на период колебаний математического маятника?
- 1.10.0.3 Как связана длина нити и период колебаний математического маятника?
- 1.10.0.4 Что происходит с периодом колебаний математического маятника при изменении массы точки?
- 1.10.0.5 Могут ли другие факторы, кроме длины нити и силы тяжести, влиять на период колебаний математического маятника?
- 1.10.0.6 Что такое математический маятник?
- 1.11 Амплитуда колебаний, влияющая на время осцилляций
- 1.12 Видео по теме:
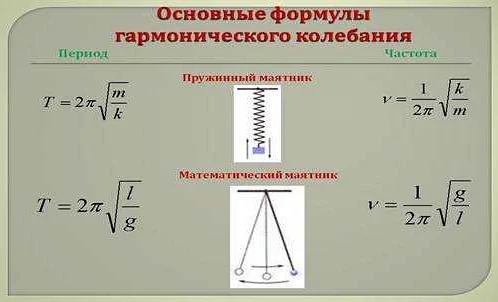
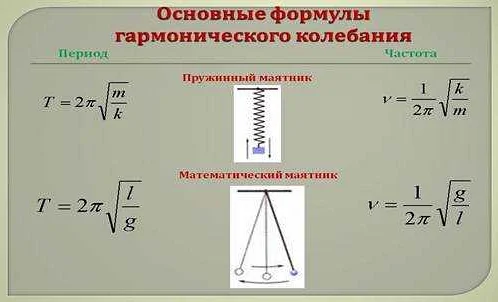
Период колебаний математического маятника зависит от его длины и силы тяжести. Чем длиннее маятник, тем больше его период. При увеличении силы тяжести период маятника уменьшается. Эти два фактора являются основными определяющими элементами для расчета периода колебаний математического маятника.
Математический маятник является одним из наиболее изученных объектов в физике. Его период колебаний, то есть время, которое требуется маятнику для одного полного оборота, зависит от нескольких факторов. Основной фактор, определяющий период, является длина маятника. Чем длиннее маятник, тем больше времени требуется на одно колебание. Это связано с тем, что при большей длине маятника увеличивается путь, который он проходит за одно колебание, и соответственно увеличивается время.
Кроме длины маятника, на период колебаний влияет ускорение свободного падения. Чем больше это ускорение, тем быстрее будет происходить колебание маятника. Величина ускорения свободного падения зависит от географического положения местности: на экваторе она больше, чем на полюсах. Также, ускорение свободного падения зависит от высоты над уровнем моря.
Масса маятника также влияет на его период колебаний. Чем больше масса маятника, тем больше сила тяжести, действующая на него. Это приводит к увеличению силы, возвращающей маятник в положение равновесия, и соответственно увеличивает период колебаний. Отметим, что масса подвеса маятника не влияет на его период колебаний.
Таким образом, период колебаний математического маятника зависит от нескольких факторов: длины маятника, ускорения свободного падения и массы маятника. Понимание этих факторов позволяет более глубоко изучить его свойства и использовать в различных практических задачах.
Влияние массы на период колебаний математического маятника
Согласно формуле периода колебаний математического маятника, T = 2π√(l/g), где T — период колебаний, l — длина подвеса маятника, g — ускорение свободного падения, можно сделать вывод, что период колебаний обратно пропорционален квадратному корню из ускорения свободного падения. Ускорение свободного падения не зависит от массы маятника и составляет примерно 9,8 м/с² на поверхности Земли.
Таким образом, влияние массы на период колебаний математического маятника заключается в том, что масса не влияет непосредственно на период колебаний, но может влиять на силу тяжести, которая действует на маятник. Более тяжелый маятник будет испытывать большую силу тяжести, что приведет к увеличению его инерции и скорости. Это может привести к увеличению периода колебаний.
Однако, если длина подвеса маятника остается постоянной, а ускорение свободного падения не изменяется, то изменение массы маятника не будет иметь значительного влияния на его период колебаний.
Таким образом, можно сказать, что масса играет относительно незначительную роль в определении периода колебаний математического маятника, поскольку этот параметр зависит в основном от длины подвеса и ускорения свободного падения.
Масса груза, определяющая период колебаний

Согласно закону Гука, период колебаний математического маятника зависит от квадратного корня из коэффициента пропорциональности между силой упругости и отклонением маятника. Этот коэффициент пропорциональности обратно пропорционален массе груза маятника.
Таким образом, с увеличением массы груза период колебаний маятника увеличивается. Более тяжелый груз создает большую силу упругости и требует больше времени для прохождения полного цикла колебаний.
Важно отметить, что зависимость между массой груза и периодом колебаний математического маятника не является линейной. Увеличение массы груза в два раза не приведет к удвоению периода колебаний. Закон Гука показывает, что изменение массы груза влияет на период колебаний известным образом.
Таким образом, масса груза является важным фактором, определяющим период колебаний математического маятника. При проведении экспериментов с маятниками необходимо учитывать массу груза и ее влияние на время осцилляций.
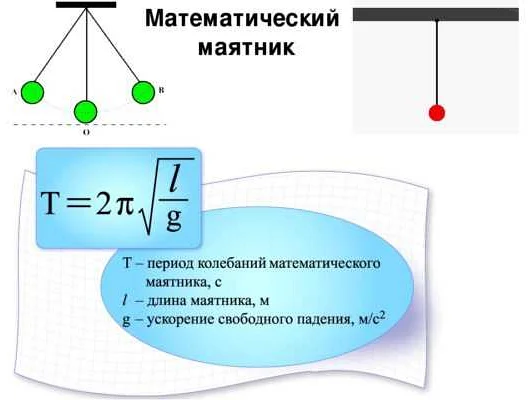
Влияние длины нити на период колебаний математического маятника
Чем длиннее нить, тем больше время, требуемое для прохождения полного колебания маятника. Это связано с тем, что при увеличении длины нити увеличивается путь, который маятник должен пройти. Следовательно, увеличивается и время, за которое он его пройдет.
Наоборот, если укоротить нить, то время периода колебаний также уменьшится. Это объясняется тем, что при уменьшении длины нити уменьшается и путь, который маятник должен пройти. Следовательно, время колебаний будет меньше.
Таким образом, можно сделать вывод, что длина нити является важным фактором, определяющим период колебаний математического маятника. При изменении длины нити меняется и время, за которое маятник совершает полное колебание. Поэтому при изучении математического маятника необходимо учитывать этот фактор.
Длина нити, влияющая на время осцилляций
Это связано с тем, что длина нити определяет период колебаний, то есть время, за которое маятник совершает одну полную осцилляцию. Формула периода колебаний математического маятника имеет вид:
T = 2π√(L/g),
где T — период колебаний, L — длина нити, g — ускорение свободного падения.
Из этой формулы видно, что период колебаний математического маятника обратно пропорционален квадратному корню из длины нити. То есть, увеличение длины нити приводит к увеличению периода колебаний.
Это связано с тем, что при увеличении длины нити увеличивается путь, который маятник должен пройти для совершения полного колебания. Следовательно, требуется больше времени для выполнения этого пути, что приводит к увеличению периода колебаний.
Длина нити также влияет на частоту колебаний математического маятника. Частота колебаний обратно пропорциональна периоду колебаний, поэтому увеличение длины нити приводит к уменьшению частоты колебаний.
Таким образом, длина нити является важным фактором, который определяет время и частоту осцилляций математического маятника. Изменение длины нити позволяет контролировать скорость и ритм колебаний, что делает этот фактор значимым при изучении и применении математического маятника.
Влияние силы трения на период колебаний математического маятника
Сила трения играет существенную роль в определении периода колебаний математического маятника. Сила трения возникает вследствие взаимодействия между маятником и окружающей средой, а именно, между маятником и воздухом или маятником и опорой, на которой он подвешен.
Влияние силы трения на период колебаний математического маятника проявляется в том, что она замедляет движение маятника, и, следовательно, увеличивает время, необходимое для совершения полного колебания. Силу трения можно представить как дополнительную силу, действующую в противоположном направлении к движению маятника.
Сила трения зависит от нескольких факторов, таких как скорость движения маятника, площадь поперечного сечения маятника, вязкость окружающей среды и другие. Более высокая скорость движения маятника приводит к увеличению силы трения, что в свою очередь увеличивает время колебаний. Площадь поперечного сечения маятника также влияет на силу трения: чем больше площадь, тем больше сила трения и, соответственно, дольше время колебаний.
Вязкость окружающей среды также оказывает влияние на силу трения и, следовательно, на период колебаний математического маятника. Чем выше вязкость, тем больше сила трения и, соответственно, дольше время колебаний.
Учет силы трения в формуле для периода колебаний математического маятника позволяет получить более точные результаты и более точное описание движения маятника в реальных условиях. Влияние силы трения на период колебаний следует учитывать при проведении экспериментов или при расчетах, связанных с колебаниями математического маятника.
Сила трения, влияющая на время осцилляций
Существует два вида трения, которые могут влиять на период колебаний математического маятника: статическое трение и динамическое трение.
Статическое трение возникает, когда поверхности между которыми осуществляется трение находятся в покое относительно друг друга. Данное трение препятствует началу движения маятника, поскольку требует дополнительной силы для преодоления сцепления между поверхностями.
Динамическое трение возникает, когда поверхности, между которыми осуществляется трение, движутся относительно друг друга. Данное трение препятствует сохранению энергии колебательной системы и приводит к затуханию колебаний во времени.
Сила трения зависит от различных факторов, таких как природа поверхностей, скорость движения маятника, сила нормального давления и другие. Чем больше трения, тем медленнее будут осцилляции маятника и тем больше времени потребуется для завершения одного полного колебания.
Важно учитывать силу трения при проведении экспериментов с математическим маятником, чтобы правильно оценить его период колебаний и сделать соответствующие выводы.
Влияние ускорения свободного падения на период колебаний математического маятника

Ускорение свободного падения обозначается символом «g» и определяется как ускорение, с которым свободно падает тело под воздействием силы тяжести. Значение ускорения свободного падения на Земле примерно равно 9,8 м/с².
Период колебаний математического маятника зависит от длины подвеса и ускорения свободного падения по следующей формуле:
ФормулаЗначение
| Период колебаний (T) | 2π√(l/g) |
где l — длина подвеса маятника.
Из этой формулы видно, что с увеличением ускорения свободного падения период колебаний математического маятника уменьшается. То есть, если ускорение свободного падения увеличивается, то маятник будет колебаться быстрее.
Таким образом, ускорение свободного падения играет важную роль в определении периода колебаний математического маятника и должно учитываться при проведении экспериментов или расчетах, связанных с этой физической системой.
Ускорение свободного падения, определяющее период колебаний
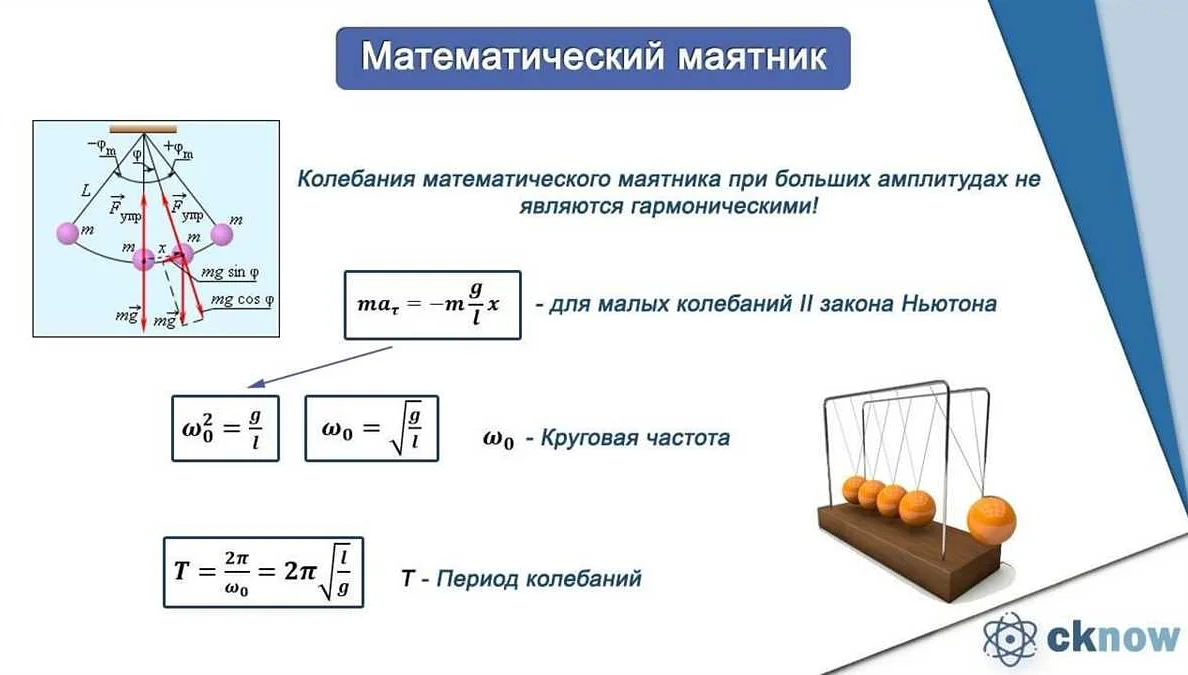
Ускорение свободного падения влияет на период колебаний математического маятника следующим образом: чем больше ускорение свободного падения, тем меньше будет период колебаний. Это связано с тем, что ускорение свободного падения определяет скорость, с которой маятник будет двигаться вниз в точке максимального отклонения.
Формула для расчета периода колебаний математического маятника включает ускорение свободного падения:
T = 2π * √(L/g)
Где T — период колебаний, L — длина математического маятника, g — ускорение свободного падения. Из этой формулы видно, что при увеличении ускорения свободного падения (g) период колебаний (T) уменьшается, так как корень из числа становится больше.
Таким образом, ускорение свободного падения играет важную роль в определении времени осцилляций математического маятника. Различные значения ускорения свободного падения на разных планетах могут привести к различным периодам колебаний, что важно учитывать при проведении экспериментов или вычислениях, связанных с математическими маятниками.
Влияние амплитуды колебаний на период математического маятника
Амплитуда колебаний — это максимальный угол отклонения маятника от положения равновесия. Чем больше амплитуда, тем больше расстояние, которое маятник должен пройти за одно колебание.
Известно, что период колебаний математического маятника можно выразить через его длину и ускорение свободного падения по формуле:
T = 2π√(l/g)
Где T — период колебаний, l — длина маятника, g — ускорение свободного падения.
Влияние амплитуды на период колебаний заключается в том, что при увеличении амплитуды, маятнику потребуется больше времени на прохождение одного колебания. Это связано с тем, что при большей амплитуде маятнику требуется больше времени на преодоление силы тяжести и изменение направления движения.
Таким образом, амплитуда колебаний математического маятника влияет на его период, и чем больше амплитуда, тем больше период колебаний.
Вопрос-ответ:
Что такое математический маятник?
Математический маятник — это абстрактная модель, которая представляет собой точку массы, подвешенную на невесомой нерастяжимой нити или стержне. Он используется для изучения основных законов колебаний.
Каковы факторы, влияющие на период колебаний математического маятника?
Период колебаний математического маятника зависит от нескольких факторов. Основными из них являются длина нити или стержня, масса точки и сила тяжести.
Как связана длина нити и период колебаний математического маятника?
Длина нити математического маятника прямо пропорциональна квадратному корню из периода колебаний. Это значит, что с увеличением длины нити период колебаний становится больше.
Что происходит с периодом колебаний математического маятника при изменении массы точки?
Масса точки математического маятника не влияет на период колебаний. Период зависит только от длины нити и силы тяжести.
Могут ли другие факторы, кроме длины нити и силы тяжести, влиять на период колебаний математического маятника?
Да, существуют и другие факторы, которые могут влиять на период колебаний математического маятника. Например, сопротивление воздуха может замедлять колебания и изменять период. Также, при больших амплитудах колебаний, их период может быть несколько отличным от периода малых колебаний.
Что такое математический маятник?
Математический маятник — это система, состоящая из точечной массы, подвешенной на невесомой нити или стержне. Он используется как модель для изучения колебаний и осцилляций.
Амплитуда колебаний, влияющая на время осцилляций
Согласно закону сохранения механической энергии, сумма потенциальной и кинетической энергии маятника остается постоянной на протяжении всего колебательного процесса. При увеличении амплитуды колебаний, потенциальная энергия также увеличивается, что приводит к увеличению кинетической энергии и скорости маятника.
Следовательно, при большей амплитуде колебаний, маятник проходит большее расстояние за один период колебаний, что приводит к увеличению времени осцилляций. В таком случае, период колебаний будет больше, чем при меньшей амплитуде.
Однако, следует отметить, что при слишком большой амплитуде колебаний возникают нелинейные эффекты, такие как деформация пружины или изменение длины маятника. Это может привести к изменению периода колебаний и ухудшению точности измерений.
Таким образом, амплитуда колебаний является важным фактором, который следует учитывать при изучении времени осцилляций математического маятника. Оптимальная амплитуда должна быть выбрана с учетом требований точности и устойчивости системы.

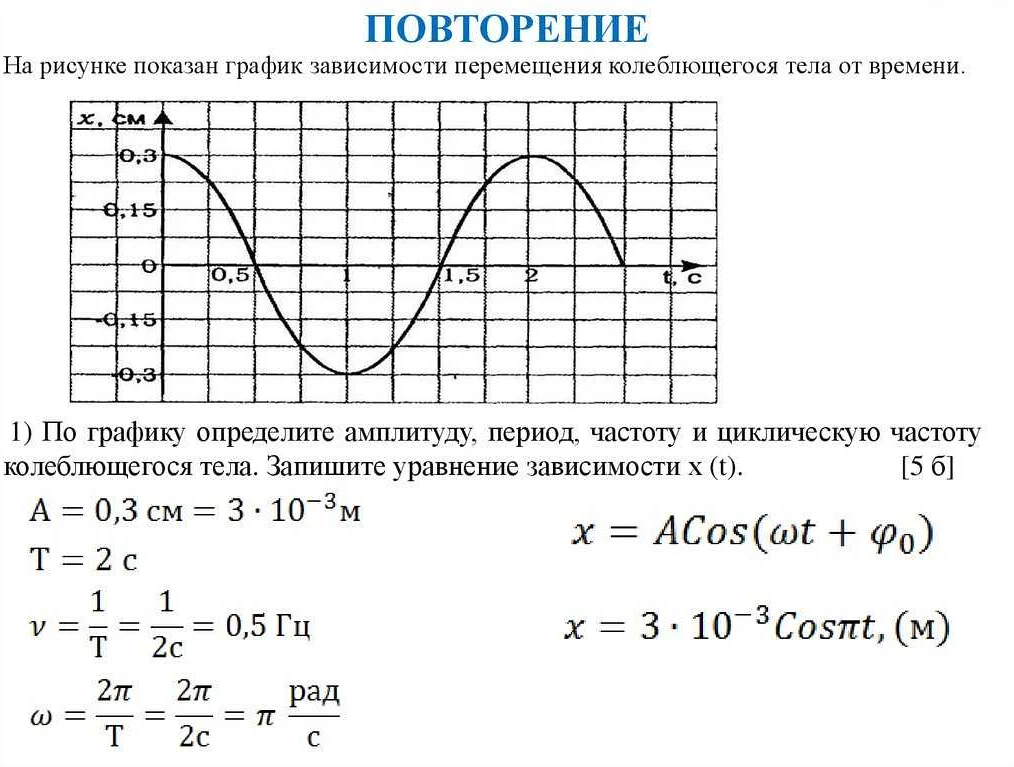

Статья очень интересная и информативная! Я всегда задавалась вопросом, от чего зависит период колебаний математического маятника. Теперь я понимаю, что на это влияет несколько факторов. Прежде всего, длина подвеса маятника — чем она больше, тем больше период колебаний. Также важным фактором является масса маятника — чем она больше, тем медленнее будет происходить колебание. И, конечно же, гравитационное поле Земли также влияет на период колебаний. Очень интересно узнать, что также влияет на период колебаний амплитуда и начальная скорость маятника. Большое спасибо за полезную информацию!