Что значит вычитать в математике

Вычитание в математике — это операция, которая позволяет находить разность между двумя числами. В процессе вычитания из одного числа вычитается другое число, что позволяет определить, насколько одно число меньше или больше другого. Узнайте подробности о том, как выполнять вычитание и его основные свойства.

Вычитание является одной из основных операций в математике, которая позволяет находить разность между двумя числами. Эта операция применяется для решения различных задач и является неотъемлемой частью арифметических операций.

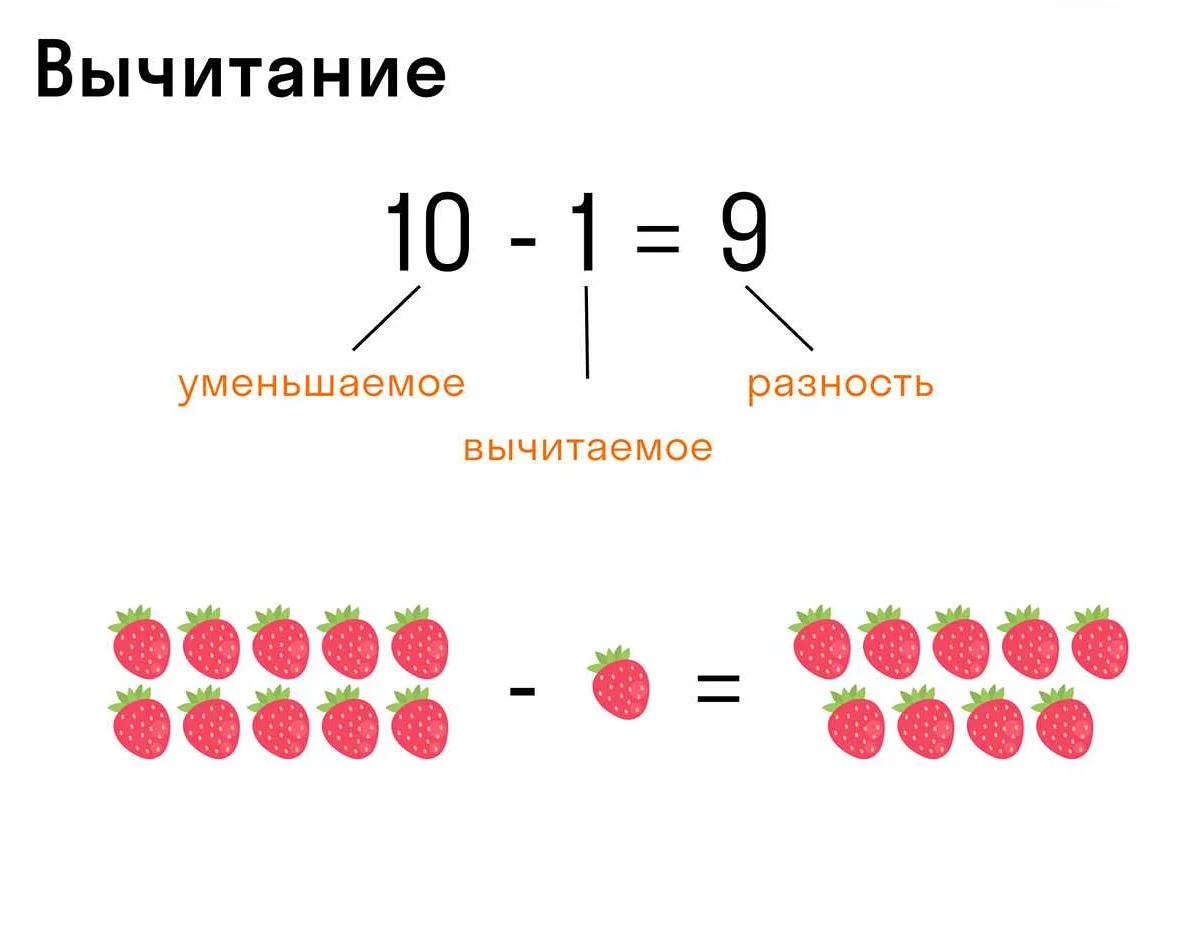
Понятие вычитания заключается в нахождении разности между уменьшаемым и вычитаемым числами. Уменьшаемое — это число, из которого вычитают. Вычитаемое — это число, которое вычитают из уменьшаемого. Результатом вычитания является разность.

Вычитание осуществляется по определенным правилам. Во-первых, если вычитаемое число положительное, а уменьшаемое — отрицательное, то вычитание превращается в сложение. Например, (-5) — (+3) = (-5) + (-3) = (-8). Во-вторых, если оба числа положительные, то вычитание осуществляется обычным образом. Например, 7 — 3 = 4. В-третьих, если вычитаемое число отрицательное, а уменьшаемое — положительное, то вычитание превращается в сложение с обратным знаком вычитаемого числа. Например, 5 — (-3) = 5 + 3 = 8.

Вычитание является важной математической операцией, которая позволяет находить разность между числами. Понимание понятия вычитания и его правил позволяет эффективно решать задачи и углублять знания в области арифметики.

Что такое вычитание в математике?

В выражении а — b, число a называется уменьшаемым, а число b – вычитаемым. Результат вычитания называется разностью.

Пример:

Рассмотрим выражение 9 — 4. В этом случае, число 9 является уменьшаемым, а число 4 – вычитаемым. Производя вычитание, получим следующую разность: 9 — 4 = 5.

При вычитании можно использовать различные стратегии, такие как вычитание в столбик или вычитание по частям. Однако, независимо от выбранного метода, результат должен быть одинаковым.

Вычитание можно использовать для решения различных задач и применять в повседневной жизни. Например, при подсчете сдачи в магазине или при решении математических задач.

Вычитание также связано с другими математическими операциями, такими как сложение и умножение. Изучение этих операций позволяет развивать навыки решения математических задач и применять их в реальной жизни.

Определение вычитания и его смысл

Вычитание представляет собой противоположную операцию сложения и осуществляется путем уменьшения одного числа на величину другого числа.

Часто в математических задачах и выражениях вычитание обозначается знаком минус (-) между числами, например: 3 — 2. При этом число, из которого вычитают, называется уменьшаемым, а число, которое вычитают, — вычитаемым.

Операция вычитания имеет свой смысл и применяется в различных сферах жизни. Она позволяет определить разность между двумя значениями, например, при измерении или расчетах. Вычитание также используется для нахождения изменений, снижений или потерь величин, а также для решения задач, связанных с сравнением и анализом данных.

Например, при измерении температуры можно вычесть текущую температуру из предыдущей, чтобы определить, насколько она изменилась. Также вычитание может быть полезно при расчете скидок или налогов, когда необходимо определить размер снижения или добавки к исходной сумме.

Понятие ориентированной разности и примеры

Пример 1:

Первая точкаВторая точкаОриентированная разность

5	2	3
2	5	-3

В первом примере, если мы вычитаем 2 из 5, получаем 3. Это означает, что первая точка находится на 3 единицы правее второй точки.

Во втором примере, если мы вычитаем 5 из 2, получаем -3. Это означает, что первая точка находится на 3 единицы левее второй точки.

Пример 2:

Первая точкаВторая точкаОриентированная разность

10	10	0
0	10	-10
10	0	10

Во втором примере, если мы вычитаем 10 из 10, получаем 0. Это означает, что обе точки совпадают и ориентированная разность равна 0.

В третьем примере, если мы вычитаем 0 из 10, получаем 10. Это означает, что первая точка находится на 10 единиц правее второй точки.

Ориентированная разность позволяет нам определить направление и расстояние между точками или числами, учитывая их порядок. Это важное понятие в математике, которое используется при решении различных задач и примеров.

Четыре основных правила вычитания

1. Вычитание числа из нуля: Результат вычитания числа из нуля всегда будет равен отрицательному значению этого числа. Например, 0 — 5 = -5.
2. Вычитание нуля из числа: Результат вычитания нуля из любого числа всегда будет равен этому числу. Например, 5 — 0 = 5.
3. Вычитание числа из самого себя: Результат вычитания числа из самого себя всегда будет равен нулю. Например, 5 — 5 = 0.
4. Вычитание двух чисел: Для выполнения вычитания двух чисел необходимо из уменьшаемого вычесть вычитаемое. Результат будет равен разности этих чисел. Например, 7 — 3 = 4.

Правильное применение этих четырех основных правил позволит вам выполнять вычитание без ошибок и получать точные результаты.

Вычитание целых чисел с примерами

Правило вычитания целых чисел гласит: если мы вычитаем положительное число из положительного, или отрицательное число из отрицательного, то мы складываем модули чисел и ставим знак минус перед результатом. Если же одно число положительное, а другое отрицательное, то вычитание сводится к сложению. Модуль числа с большим по абсолютной величине значением пишется первым.

Например, если мы хотим найти разность между числами 5 и 3, мы вычитаем модуль числа 3 из модуля числа 5: 5 — 3 = 2. В данном случае числа являются положительными, поэтому результат также будет положительным.

Если мы хотим найти разность между числами -8 и -12, мы сначала найдем модуль для каждого числа и затем сложим их: |-8| + |-12| = 8 + 12 = 20. Так как оба числа являются отрицательными, то результат будет отрицательным.

Если мы хотим найти разность между числами -6 и 9, мы сначала найдем модуль для каждого числа и затем сложим их: |-6| + 9 = 6 + 9 = 15. Одно число отрицательное, а другое положительное, поэтому результат будет положительным.

Вычитание целых чисел является важным навыком и может применяться в различных ситуациях, как в повседневной жизни, так и в других областях, например, в финансовой математике или программировании.

Вычитание десятичных чисел с примерами

Вычитание десятичных чисел выполняется по тому же принципу, что и вычитание целых чисел. Но в данном случае мы работаем с числами, которые имеют десятичную часть.

Правила вычитания десятичных чисел следующие:

1. Выполняем вычитание по правилам вычитания целых чисел.
2. Если в результате вычитания дробная часть числа получается отрицательной, занимаем единицу из целой части числа слева от дробной части и прибавляем ее к отрицательной дробной части.

Рассмотрим несколько примеров вычитания десятичных чисел:

Пример 1:

Вычтем 4.2 из 7.9.

7.9 — 4.2 = 3.7

Пример 2:

Вычтем 13.7 из 35.9.

35.9 — 13.7 = 22.2

Пример 3:

Вычтем 0.6 из 1.8.

1.8 — 0.6 = 1.2

Таким образом, вычитание десятичных чисел может быть выполнено с помощью правил вычитания целых чисел, с учетом особенностей десятичной части чисел. При необходимости можно занимать единицу из целой части и прибавлять ее к отрицательной дробной части.

Вычитание дробей: сведение к общему знаменателю и упрощение

Для сведения дробей к общему знаменателю можно воспользоваться несколькими способами. Один из них – использование наименьшего общего кратного (НОК) знаменателей дробей. Для этого необходимо найти НОК знаменателей и заменить исходные дроби эквивалентными, у которых знаменатели равны НОК. После этого можно произвести вычитание числителей и записать результат в виде дроби с общим знаменателем.

Полученную дробь можно упростить, если она не является несократимой. Для этого необходимо найти наибольший общий делитель (НОД) числителя и знаменателя дроби. Если НОД больше единицы, то можно разделить числитель и знаменатель на НОД, получив тем самым эквивалентную дробь, которую уже нельзя упростить.

Вычитание с остатком и его применение

Для выполнения вычитания с остатком необходимо применить следующие правила:

1. Если вычитаемое больше уменьшаемого, то остаток будет отрицательным числом. Например, при вычитании 7 из 4, получаем -3 в качестве остатка.
2. Если цифра, стоящая перед вычитаемым числом, меньше цифры, стоящей перед уменьшаемым числом, необходимо занять единицу из предыдущего разряда. Например, при вычитании 25 из 37, необходимо занять единицу из разряда десятков, получая остаток 12.
3. Если цифра, стоящая перед вычитаемым числом, равна цифре, стоящей перед уменьшаемым числом, и при этом вычитаемое больше уменьшаемого, также необходимо занять единицу из предыдущего разряда. Например, при вычитании 37 из 37, необходимо занять единицу из разряда десятков, получая остаток 0.

Вычитание с остатком на практике используется в различных областях, включая финансы, бухгалтерию, программирование и другие. Например, при расчете разницы между двумя датами, вычитание с остатком позволяет получить количество дней, часов, минут и секунд, которые прошли с момента начала до момента окончания.

Вопрос-ответ:

Что такое вычитание в математике?

Вычитание — это одна из основных операций в математике, которая используется для нахождения разности между двумя числами. При вычитании одного числа из другого мы находим значение, которое нужно прибавить к вычитаемому числу, чтобы получить уменьшаемое число.

Какие правила нужно знать для выполнения вычитания?

Для выполнения вычитания нужно знать несколько правил. Во-первых, при вычитании чисел разного знака, мы меняем знак у вычитаемого числа и выполняем сложение. Во-вторых, при вычитании большего числа из меньшего, результат будет отрицательным. В-третьих, при вычитании числа из нуля, результат будет противоположным вычитаемому числу.

Как выполнить вычитание с переносом?

Вычитание с переносом выполняется, когда разряд разности в одном столбце меньше нуля. В этом случае нужно занять единицу от следующего старшего разряда и увеличить разряд разности на 10. Затем продолжаем вычитание, учитывая этот перенос.

Как выполнить вычитание с десятичными дробями?

Вычитание с десятичными дробями выполняется по тем же правилам, что и вычитание с целыми числами. Мы вычитаем каждую десятичную цифру по отдельности, начиная с самой правой. Если после вычитания получается отрицательное число, мы занимаем 1 от следующей десятичной цифры и увеличиваем разряд разности на 10.

Чему равен результат вычитания нуля из числа?

Результат вычитания нуля из любого числа равен этому числу. Вычитание нуля не меняет значение числа, поэтому разница будет равна вычитаемому числу.

Что такое вычитание в математике?

Вычитание — это одна из основных арифметических операций, которая позволяет находить разность двух чисел или выражений. В результате вычитания получается число или выражение, которое является результатом отнимания одного числа или выражения от другого.

Видео по теме: