Что такое вычитать в математике
Содержимое
- 1 Что такое вычитать в математике
- 1.1 Определение вычитания
- 1.2 Значение вычитания в математике
- 1.3 Основные понятия вычитания
- 1.4 Вычитаемое и уменьшаемое
- 1.5 Разность
- 1.6 Отрицательные числа
- 1.7 Правила вычитания
- 1.8 Правило вычитания чисел с одинаковым знаком
- 1.9 Вопрос-ответ:
- 1.9.0.1 Как выполняется вычитание в математике?
- 1.9.0.2 Какие основные понятия связаны с вычитанием в математике?
- 1.9.0.3 Какие правила существуют для выполнения вычитания в математике?
- 1.9.0.4 Можете привести примеры вычитания?
- 1.9.0.5 Какие проблемы могут возникнуть при выполнении вычитания?
- 1.9.0.6 Какие основные понятия связаны с вычитанием в математике?
- 1.10 Правило вычитания чисел с разными знаками
- 1.11 Видео по теме:
Вычитание в математике — это арифметическая операция, которая позволяет находить разность между двумя числами. При вычитании одно число вычитается из другого, что позволяет определить, сколько остается после отнимания. Узнайте, как правильно выполнять вычитание и как применять его в повседневной жизни.
Вычитание является одной из основных операций в математике, которая позволяет находить разность между двумя числами. Оно широко используется в повседневной жизни и в различных областях науки.
Основное понятие вычитания заключается в том, что при вычитании одного числа из другого мы находим разницу между ними. Первое число называется уменьшаемым, а второе — вычитаемым. Результат вычитания называется разностью.
Правила вычитания определяют порядок действий и позволяют выполнять вычитание с учетом знаков чисел. Если вычитаемое число положительное, то вычитание сводится к добавлению его противоположного числа. Если вычитаемое число отрицательное, то вычитание сводится к сложению его с противоположным числом.
Пример: 10 — 5 = 10 + (-5) = 5
Вычитание также связано с другими арифметическими операциями, такими как сложение, умножение и деление. Понимание основных понятий и правил вычитания является важным для решения математических задач и развития логического мышления.
Определение вычитания
Вычитание в математике обозначается знаком «-«, который ставится между уменьшаемым и вычитаемым числами. Например, вычитание числа 7 из числа 10 записывается как 10 — 7. Результатом данного вычитания будет число 3, так как 10 уменьшается на 7.
Правила вычитания определяют, что если вычитаемое положительное, то результат вычитания будет меньше уменьшаемого числа. Если вычитаемое отрицательное, то результат вычитания будет больше уменьшаемого числа. Если вычитаемое равно 0, то результатом вычитания будет само уменьшаемое число.
Например, при вычитании числа 5 из числа 10, результатом будет число 5, так как 10 уменьшается на 5. А при вычитании числа -3 из числа 10, результатом будет число 13, так как 10 увеличивается на 3.
Значение вычитания в математике

Значение вычитания можно представить с помощью таблицы:
МинуэндВычитаемоеРазность
| уменьшаемое | вычитатель | разность |
Минуэнд — это число, из которого вычитают. Вычитаемое — это число, которое вычитают из минуэнда. Разность — это результат вычитания, то есть полученное число.
Правила вычитания:
- Вычитаемое вычитается из минуэнда слева направо, начиная с разряда единиц.
- Если в разряде, из которого происходит вычитание, вычитаемое больше минуэнда, то необходимо занять единицу из старшего разряда.
- Если вычитаемое равно нулю, то разность равна минуэнду.
Вычитание является важной математической операцией, которая применяется в различных областях науки и повседневной жизни. Оно позволяет решать задачи, связанные с расчетами, уменьшением, отрицательными значениями и другими аспектами числовых операций.
Основные понятия вычитания
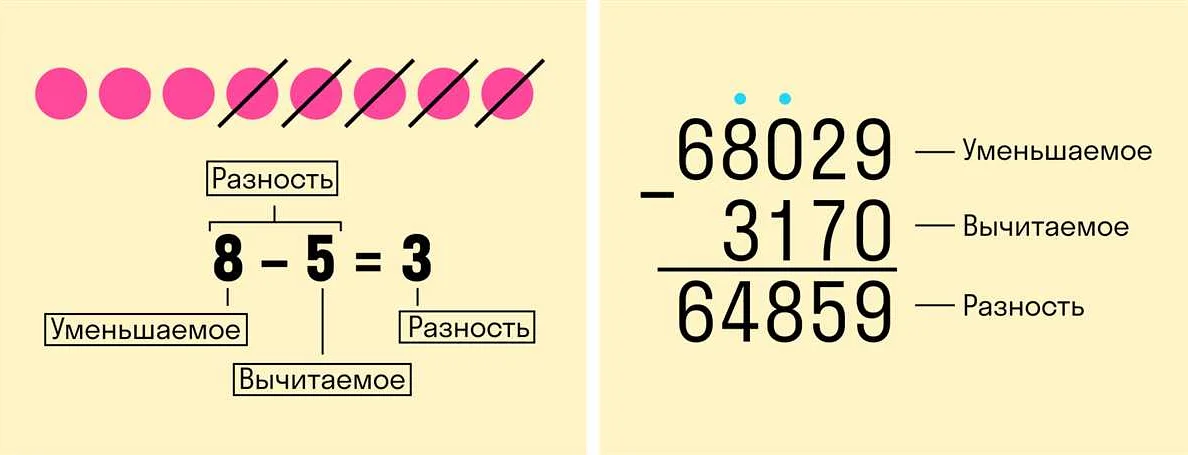
Вычитаемое — это число, которое вычитают из другого числа, называемого уменьшаемым. Ответ на вычитание называется разностью.
Правило вычитания гласит, что разность двух чисел равна разности их цифр в соответствующих разрядах. Если цифра в вычитаемом больше цифры в уменьшаемом, то из цифры в следующем разряде «заимствуют» единицу, чтобы выполнить вычитание.
Например:
- 3 — 2 = 1
- 8 — 5 = 3
- 12 — 8 = 4
- 25 — 17 = 8
При работе с многоразрядными числами вычитание проводят поэтапно, начиная с младших разрядов и двигаясь к старшим. При этом, если в столбике вычитаемое больше уменьшаемого, выполняется заимствование единицы. Это делается до тех пор, пока все разряды не будут вычтены.
Вычитание можно записать в виде столбика, где вычитаемое располагается под уменьшаемым, а разность выписывается под ними. Каждый разряд числа должен быть выведен в своей колонке.
Вычитаемое и уменьшаемое

Вычитаемое — это число, которое вычитают из другого числа. Оно является одним из компонентов вычитания и находится перед знаком вычитания (-).
Уменьшаемое — это число, из которого вычитают вычитаемое. Оно является другим компонентом вычитания и находится после знака вычитания (-).
Например, в выражении 7 — 3 = 4, число 3 является вычитаемым, а число 7 — уменьшаемым.
Вычитаемое и уменьшаемое могут быть как положительными, так и отрицательными числами. В данном случае, при вычитании положительного числа из отрицательного, результат будет отрицательным числом.
Разность
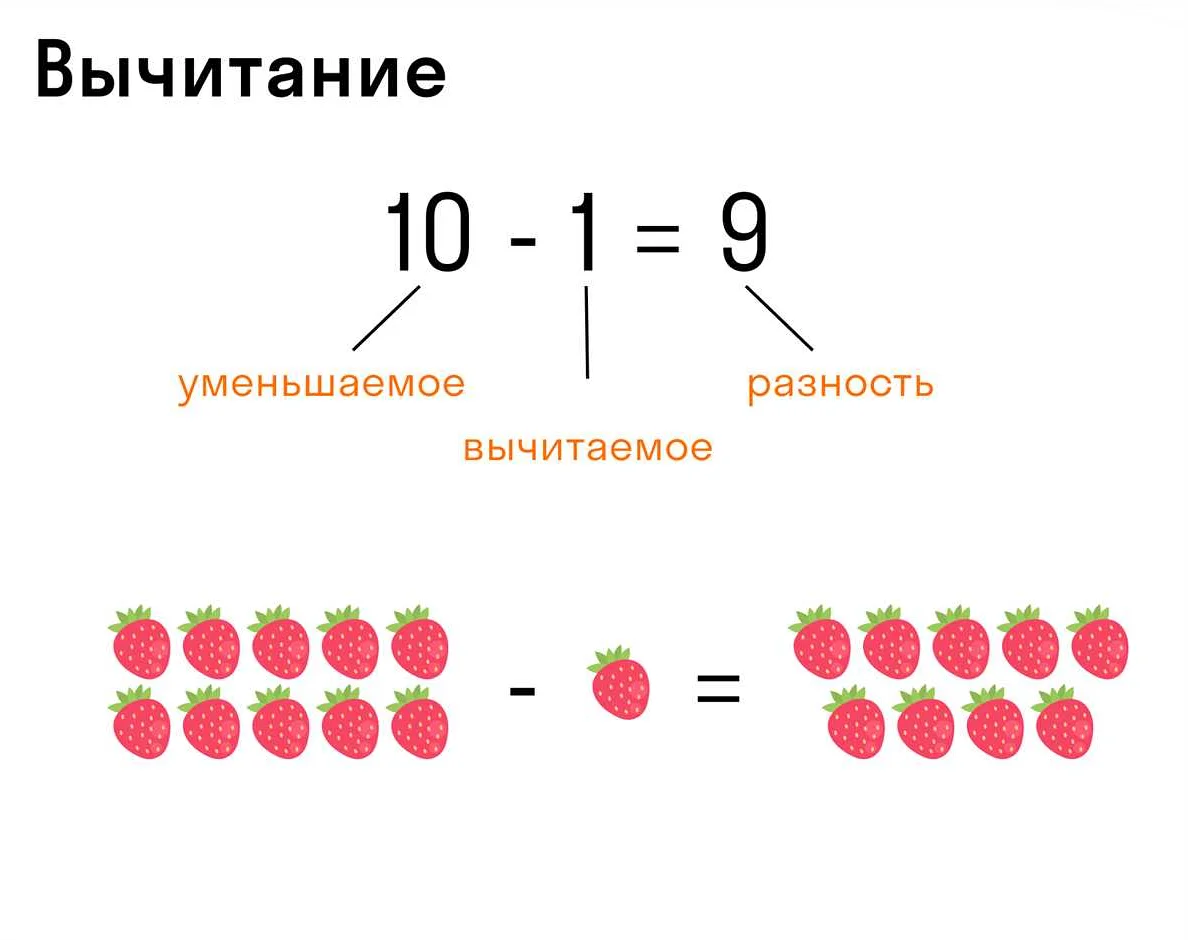
Вычитание можно представить с помощью вычитательной записи. Вычитательная запись представляет собой символ вычитания (-) между вычитаемым и вычитателем, а результат вычитания записывается после символа равенства (=).
Например, при вычитании числа 5 из числа 9, вычитательная запись будет выглядеть так: 9 — 5 = 4. В данном случае 9 – это вычитаемое, 5 – это вычитатель, а 4 – это результат вычитания, то есть разность между числами 9 и 5.
Правила вычитания помогают выполнить вычитание правильно и получить корректный результат:
- Вычитаемое всегда располагается перед вычитателем.
- Если вычитаемое меньше вычитателя, то в результате вычитания получится отрицательное число. Например, если вычесть 7 из 3, то результат будет -4.
- Если вычитаемое равно вычитателю, то результат вычитания будет равен 0. Например, 8 — 8 = 0.
- Вычитание можно выполнить путем добавления числа, обратного вычитаемому. Например, чтобы вычесть 9 из 14, можно сложить число 14 и число -9, так как -9 является обратным числом для 9.
Вычитание необходимо для решения различных задач и задачек, а также для выполнения сложнее математических операций, таких как умножение и деление. Понимание концепции вычитания и умение применять правила вычитания поможет в освоении более сложных математических тем и задач.
Отрицательные числа
Отрицательные числа могут быть использованы в различных математических операциях, включая вычитание. Вычитание отрицательных чисел имеет свои особенности и правила.
Правило вычитания отрицательного числа: чтобы вычесть отрицательное число, его знак меняется на противоположный и выполняется обычное сложение. Например, чтобы вычесть -5 из 10, меняем знак у -5 на плюс и складываем: 10 + 5 = 15.
Отрицательные числа также используются для обозначения направления или задания отрицательных величин. Например, при измерении температуры ниже нуля используются отрицательные числа.
Отрицательные числа играют важную роль в математике и имеют множество применений в реальном мире. Понимание основных концепций и правил вычитания отрицательных чисел помогает строить более сложные математические выражения и решать различные задачи.
Правила вычитания

- Метод переноса: если разряд уменьшаемого числа меньше разряда вычитаемого числа, то необходимо выполнить перенос. Это означает, что нужно занять единицу из старшего разряда и уменьшить его значение на единицу.
- Вычитание по разрядам: сначала вычитаются цифры в одинаковых разрядах, начиная с самого правого разряда. Если цифра уменьшаемого числа меньше цифры вычитаемого числа, то выполняется перенос и занимается единица из следующего разряда.
- Вычитание нуля: любое число, вычитаемое из нуля, остается без изменений. То есть, вычитание нуля не влияет на значение числа.
Соблюдение этих правил позволяет правильно выполнять вычитание и получать верный результат. При решении задач с вычитанием также важно учитывать порядок выполнения операций и действовать последовательно.
Правило вычитания чисел с одинаковым знаком
Правило вычитания чисел с одинаковым знаком основано на свойствах алгебры и позволяет найти разность между двумя числами, если они имеют одинаковый знак.
Когда мы вычитаем два числа с одинаковым знаком (положительное и положительное или отрицательное и отрицательное), мы складываем их модули и сохраняем знак исходных чисел:
- Если оба числа положительные, то вычитание будет иметь положительный результат.
- Если оба числа отрицательные, то вычитание будет иметь отрицательный результат.
Например, чтобы вычесть 5 из 8, мы складываем модули этих чисел: |8| — |5| = 8 — 5 = 3. Так как оба числа положительные, результат будет положительным.
Аналогично, чтобы вычесть -3 из -7, мы складываем модули этих чисел: |-7| — |-3| = 7 — 3 = 4. Так как оба числа отрицательные, результат будет отрицательным.
Правило вычитания чисел с одинаковым знаком может быть использовано для решения различных задач и примеров, включая работу с долгами и температурой.
Вопрос-ответ:
Как выполняется вычитание в математике?
Вычитание в математике выполняется путем вычитания одного числа из другого. Для этого необходимо выравнять числа по разрядам и вычислить разность между соответствующими разрядами.
Какие основные понятия связаны с вычитанием в математике?
Основными понятиями, связанными с вычитанием в математике, являются уменьшаемое (число, из которого вычитают), вычитаемое (число, которое вычитают) и разность (результат вычитания).
Какие правила существуют для выполнения вычитания в математике?
Основные правила вычитания в математике включают выравнивание чисел по разрядам, вычитание разрядов, перенос и замену нулей. Также важно запомнить, что вычитание не коммутативно (порядок чисел важен) и что разность может быть как положительной, так и отрицательной.
Можете привести примеры вычитания?
Конечно! Например, 7 — 3 = 4, где 7 — уменьшаемое, 3 — вычитаемое, 4 — разность. Еще один пример: 15 — 8 = 7. Здесь 15 — уменьшаемое, 8 — вычитаемое, 7 — разность.
Какие проблемы могут возникнуть при выполнении вычитания?
При выполнении вычитания могут возникнуть проблемы, связанные с неправильным выравниванием разрядов, ошибками при вычитании разрядов и неправильным переносом. Также важно не забыть учесть правила замены нулей и порядок чисел при вычитании.
Какие основные понятия связаны с вычитанием в математике?
Вычитание в математике связано с такими основными понятиями, как уменьшаемое, вычитаемое и разность. Уменьшаемое — это число, из которого производится вычитание. Вычитаемое — число, которое вычитается из уменьшаемого. Разность — результат вычитания, полученное число.
Правило вычитания чисел с разными знаками
При вычитании чисел с разными знаками необходимо следовать определенным правилам. Изначально необходимо определить знак результата. Если уменьшаемое число положительное, а вычитаемое число отрицательное (или наоборот), то знак результата будет соответствовать знаку большего по модулю числа. Например, при вычитании -8 из 5, знак результата будет отрицательным, так как 8 больше по модулю, чем 5.
Далее следует выполнить вычитание по модулю, то есть игнорировать знаки чисел и вычислить разницу по абсолютной величине. Например, 5 — (-8) равняется 5 + 8 = 13.
В конечном итоге результат будет иметь знак, определенный на первом шаге. В нашем примере, -13.
Если уменьшаемое и вычитаемое числа имеют одинаковые знаки, следует выполнить сложение по модулю и присвоить результату знак, соответствующий знаку исходных чисел. Например, при вычитании 5 из 8, результат будет положительным, так как и уменьшаемое, и вычитаемое числа положительные.

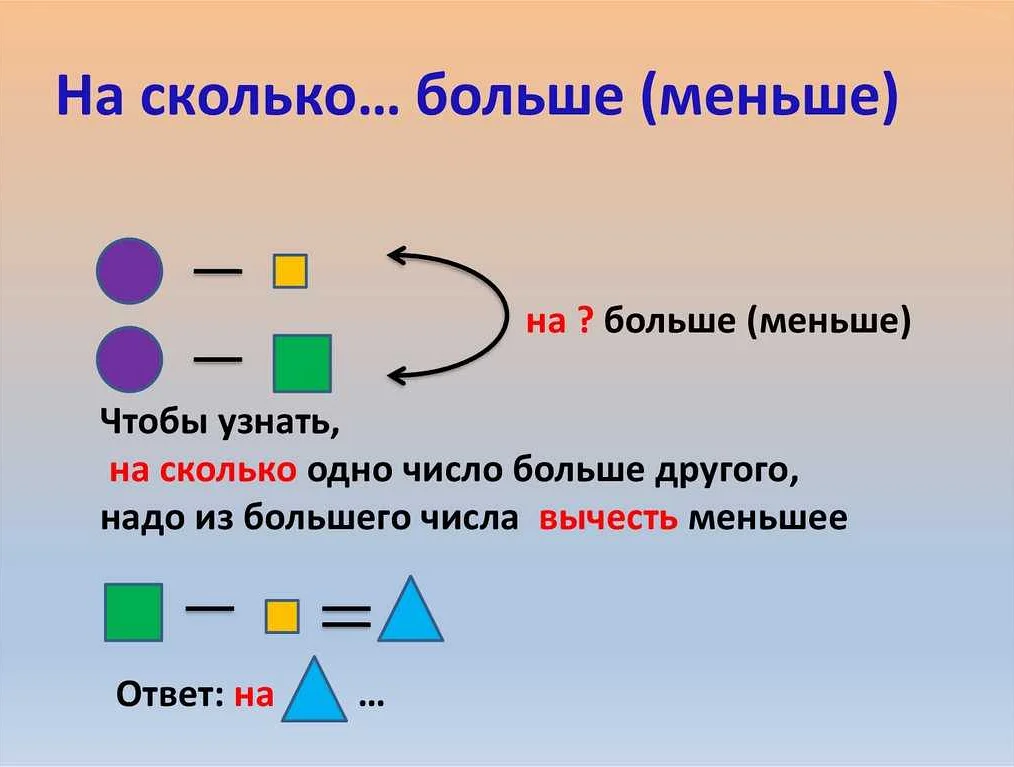


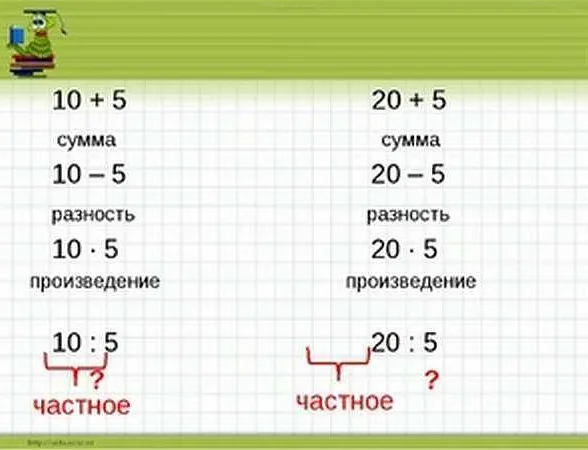
Вычитание в математике – одна из основных арифметических операций, с помощью которой мы находим разность двух чисел. Все начинается с понятия уменьшаемого и вычитаемого. Уменьшаемое – это число, от которого мы будем отнимать. Вычитаемое – это число, которое мы будем вычитать из уменьшаемого. Результатом вычитания будет разность этих чисел. Правила вычитания несложны. Вначале мы выравниваем числа по разрядам, а затем начинаем вычитать. Если вычитаемое меньше уменьшаемого, то просто вычитаем цифры столбиком, начиная с самого правого разряда. Если же вычитаемое больше уменьшаемого, то приходится занимать единицу из следующего разряда и продолжать вычитание. Вычитание – это важный навык, который пригодится нам не только в математике, но и в повседневной жизни. Например, когда мы считаем сдачу в магазине или вычитаем время, чтобы определить, сколько времени мы провели на занятии. Понимание основных понятий и правил вычитания помогает нам развивать наши навыки в математике и улучшать наше понимание чисел и операций с ними.
Вычитание — это одна из основных арифметических операций в математике, которая позволяет находить разность между двумя числами. Это важное умение, которое пригодится не только в школе, но и в повседневной жизни. Правила вычитания достаточно просты. Необходимо вычесть меньшее число из большего. Если мы вычитаем числа, которые имеют одинаковый знак (положительный или отрицательный), то просто складываем их модули и приписываем результат тому же знаку. Например, 5 — 3 = 2, -7 — (-2) = -5. Если числа имеют разный знак, то вычитание сводится к сложению чисел с противоположными знаками. Например, 5 — (-3) = 5 + 3 = 8. Вычитание также возможно с десятичными и дробными числами. В этом случае необходимо вычитать цифру за цифрой, начиная справа. Если в уменьшаемом число меньше, чем в вычитаемом, то необходимо занять единицу из старшего разряда. Вычитание — это важный навык, который нужно уметь применять в решении разнообразных математических задач. Понимание основных правил вычитания поможет вам справиться с этой операцией легко и быстро.
Статья прекрасно объясняет основные понятия вычитания в математике. Очень понятно и доступно написано о том, что вычитание — это операция, обратная сложению, и оно позволяет находить разность двух чисел. Мне особенно понравилось, как автор пошагово описал правила вычитания, начиная от простых случаев и переходя к более сложным. Ясно и понятно объяснено, что уменьшаемое вычитается из уменьшителя, а разность получается в результате. Также автор указал на важность правильного выбора знака при вычитании отрицательных чисел. Я узнал много нового и теперь лучше понимаю, как работает вычитание. Рекомендую всем, кто желает усовершенствовать свои знания в математике.
Статья очень понятно и доступно объясняет основные понятия и правила вычитания. Я всегда путалась в этой операции, но теперь все стало гораздо проще! Особенно мне понравилось, как автор подробно разобрал случаи с вычитанием нуля и вычитанием отрицательных чисел. Теперь я точно знаю, что результат вычитания нуля равен самому вычитаемому числу, а при вычитании отрицательного числа мы прибавляем к исходному числу модуль этого числа. Статья очень полезна и хорошо структурирована, я теперь точно буду лучше разбираться с вычитанием!