Что такое вычитаемое в математике

Вычитаемое в математике — это число или выражение, которое вычитается из другого числа или выражения. Узнайте, как определить вычитаемое и выполнить вычитание в математике.

Вычитаемое — одно из основных понятий в математике, которое используется в операции вычитания. Определение этого термина представляет собой число или выражение, которое вычитают из другого числа или выражения, называемого уменьшаемым.

Вычитаемое в операции вычитания всегда указывается после знака минус, который обозначает вычитание. Это значит, что вычитаемое является вторым компонентом этой операции. Например, в выражении «10 — 5», число 5 является вычитаемым, так как его вычитают из числа 10.

Особенностью вычитаемого является его влияние на результат операции вычитания. Если вычитаемое положительное, то оно уменьшает значение уменьшаемого. Например, «10 — 5 = 5». Если же вычитаемое отрицательное, то оно увеличивает значение уменьшаемого. Например, «10 — (-5) = 15».

Примеры:

Пример 1: 12 — 7 = 5

Пример 2: 20 — (-4) = 24

Пример 3: x — y = z

Вычитаемое имеет важное значение в математике, так как операция вычитания широко применяется в различных областях, например, при решении уравнений и задач по арифметике. Понимание и правильное использование данного понятия позволяет проводить точные вычисления и получать верные результаты.

Определение вычитаемого в математике

Вычитаемое может быть положительным, отрицательным или нулевым числом, а также может быть выражено с использованием переменных или других математических операций. В зависимости от конкретной задачи или контекста, вычитаемое может иметь различные значения и свойства.

Например, при выполнении простого вычитания «5 — 3», число 3 является вычитаемым, так как оно вычитается из числа 5. В этом случае, вычитаемое равно 3.

В общем смысле, вычитаемое представляет собой значение или элемент, который уменьшается или вычитается из другого числа или выражения. Оно помогает определить конечный результат операции вычитания и может влиять на ответ или решение задачи.

Вычитаемое — это число или выражение, которое вычитается из другого числа или выражения в математической операции вычитания.

Например, в выражении 10 — 5, число 5 является вычитаемым. Результатом операции будет число 5, так как мы вычитаем 5 из 10.

Вычитаемое может быть как положительным, так и отрицательным числом. Если вычитаемое положительное, то оно уменьшает значение изначального числа. Если вычитаемое отрицательное, то оно увеличивает значение изначального числа. Например, в выражении 10 — (-5), число -5 является вычитаемым и будет складываться с 10, что приведет к результату 15.

В математических выражениях вычитаемое может быть также в виде выражения, содержащего переменные и операторы. Например, в выражении x — (2y + z), вычитаемым является выражение (2y + z), которое будет вычисляться в зависимости от значений переменных y и z.

Вычитаемое играет важную роль в математике и позволяет выполнять операции вычитания для нахождения разности между числами или выражениями.

Примеры вычитаемого в математике

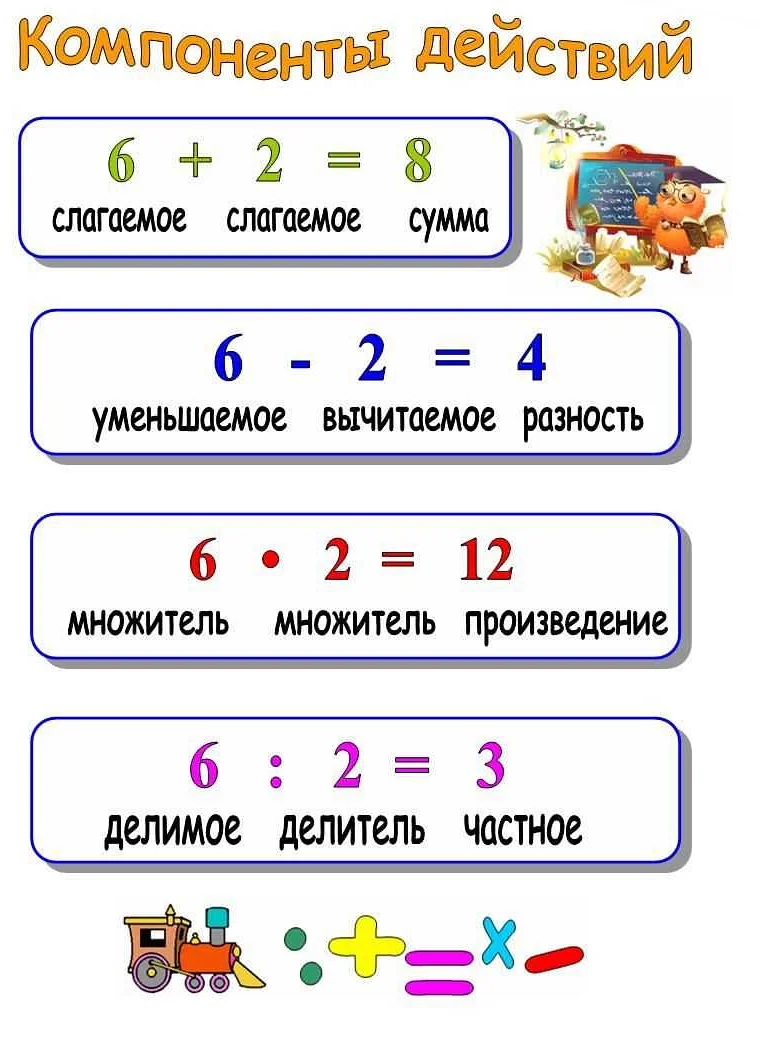
Пример 1: В выражении 9 — 4 = 5, число 4 является вычитаемым.

Пример 2: Если у нас есть выражение a — b = c, где a = 7, b = 2 и c = 5, то число 2 является вычитаемым.

Пример 3: В уравнении x — 3 = 8, число 3 является вычитаемым.

Вычитаемое может быть как положительным, так и отрицательным числом. Оно может быть представлено как числом, переменной или комбинацией чисел и переменных.

Обрати внимание, что порядок чисел и выражений в операции вычитания имеет значение. Вычитаемое всегда идет перед вычитающим числом или выражением.

Пример 1: Вычитаемое в простой операции — 5 из 10.

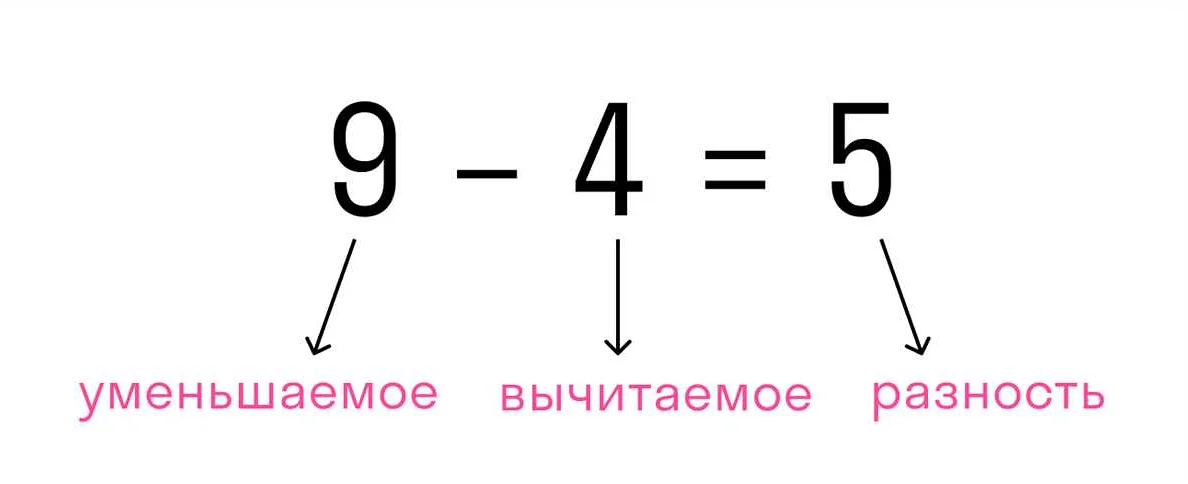
Вычитаемое в данном случае равно 5, так как это число, которое мы вычитаем из другого числа, называемого уменьшаемым или уменьшаемым числом.

Таким образом, если мы вычтем 5 из 10, получим результат 5.

Пример 2: Вычитаемое может быть переменной или выражением — x^2 — 3x + 2.

Для вычисления разности двух чисел или выражений, в данном случае разности x^2 — 3x + 2 и вычитаемого, необходимо учесть знак перед вычитаемым и выполнить соответствующие арифметические операции.

ВычитаемоеВычитаемоеРазность

x^2 — 3x + 2

—

вычитаемое

В данном примере переменная x может принимать различные значения, и результат разности будет зависеть от этих значений.

Особенности вычитаемого в математике

Основная особенность вычитаемого заключается в том, что оно определяет, насколько будет уменьшаться уменьшаемое число. В контексте математики вычитаемое может быть любым числом, включая натуральные и целые числа, дроби и десятичные дроби.

При вычитании двух чисел, вычитаемое может быть больше, меньше или равно уменьшаемому. В случае, если вычитаемое больше уменьшаемого, получается отрицательная разность. Если вычитаемое равно уменьшаемому, разность будет равна нулю. Если вычитаемое меньше уменьшаемого, получается положительная разность.

Определение и выбор вычитаемого зависит от поставленной задачи или конкретной математической операции. Например, при решении задач на вычитание десятичных дробей, вычитаемое может быть представлено в виде десятичной дроби с определенным числом знаков после запятой.

Также стоит учитывать, что при вычитании больших чисел с различным количеством разрядов, вычитаемое может иметь дополнительные цифры или нули в начале, чтобы обеспечить правильную позицию цифр при выполнении операции вычитания.

Особенность 1: Вычитаемое может быть как положительным, так и отрицательным числом.

Если вычитаемое число положительное, то результатом вычитания будет отрицательное число. Например, если вычесть из 5 число 3, то получится -2.

Если же вычитаемое число отрицательное, то результатом вычитания будет положительное число. Например, если вычесть из 5 число -3, то получится 8.

Такая особенность вычитаемого позволяет производить различные операции с числами и получать разные результаты в зависимости от знака вычитаемого числа.

Особенность 2: Вычитаемое может быть больше или меньше уменьшаемого числа или выражения.

В математике при вычитании одного числа из другого, вычитаемое может быть как больше, так и меньше уменьшаемого числа или выражения. Эта особенность открывает возможности для различных ситуаций и задач.

Если вычитаемое больше уменьшаемого числа или выражения, то результат будет отрицательным числом или выражением. Например, если из числа 7 вычесть число 10, результат будет -3:

ВычитаемоеУменьшаемоеРезультат

10

7

-3

Если же вычитаемое меньше уменьшаемого числа или выражения, то результат будет положительным числом или выражением. Например, если из числа 10 вычесть число 7, результат будет 3:

ВычитаемоеУменьшаемоеРезультат

7

10

3

Таким образом, вычитаемое может быть как больше, так и меньше уменьшаемого числа или выражения, и это влияет на знак и значение результата вычитания.

Вопрос-ответ:

Что такое вычитаемое в математике?

Вычитаемое — это число или выражение, которое вычитается из другого числа или выражения в математической операции вычитания.

Как определить вычитаемое в математике?

Вычитаемое определяется в математике как число или выражение, которое должно быть вычтено из другого числа или выражения в операции вычитания. Обычно вычитаемое указывается после знака минус (-) в выражении.

Какие примеры вычитаемых чисел?

Примерами вычитаемых чисел могут быть любые числа, которые должны быть вычтены из других чисел. Например, в выражении 5 — 3, число 3 является вычитаемым, так как оно вычитается из числа 5.

Можно ли использовать выражения как вычитаемые числа?

Да, можно использовать выражения как вычитаемые числа. Например, в выражении 10 — (2 + 3), выражение (2 + 3) является вычитаемым, так как оно вычитается из числа 10.

Какие особенности связаны с вычитаемым в математике?

Одной из особенностей, связанных с вычитаемым в математике, является то, что порядок чисел в операции вычитания влияет на результат. Например, при вычитании 3 из 5 мы получим разный результат, чем при вычитании 5 из 3. Также стоит помнить, что вычитаемое может быть как положительным, так и отрицательным числом.

Особенность 3: Вычитаемое может быть представлено как дробью или корнем.

При вычитании чисел может возникнуть ситуация, когда вычитаемое будет представлено в виде дроби или корня. В таких случаях необходимо применять специальные правила и методы для выполнения вычитания.

Если вычитаемое представлено в виде дроби, то необходимо привести оба вычитаемое и уменьшаемое к общему знаменателю. Затем можно произвести вычитание числителей и оставить общий знаменатель.

Пример:

Вычтем 3/4 из 5/6:

• Приведем дроби к общему знаменателю, который равен 12.
• 5/6 = 10/12
• 3/4 = 9/12
• Теперь можно произвести вычитание числителей: 10/12 — 9/12 = 1/12
• Ответ: 1/12

Если вычитаемое представлено в виде корня, то необходимо применять правила работы с корнями. Для выполнения вычитания корней можно использовать свойства корней и приведение подобных выражений.

Пример:

Вычтем √5 из √8:

• Преобразуем корни к подобным выражениям: √8 = √(4 * 2) = √4 * √2 = 2√2
• Теперь можно произвести вычитание: 2√2 — √5
• Ответ: 2√2 — √5

Таким образом, вычитаемое в математике может быть представлено как дробью или корнем, и для выполнения вычитания необходимо применять соответствующие правила и методы в зависимости от представления вычитаемого.

Видео по теме: