Что такое диаграмма венна в математике

Диаграмма Венна — это визуальный инструмент в математике, который помогает представить пересечение и отношения между различными множествами. Узнайте, как использовать диаграмму Венна для анализа данных и решения задач в математике.

Диаграмма Венна — это графическое представление множества и их отношений, которое было введено английским математиком Джоном Венном в 1880-х годах. Она позволяет наглядно отображать пересечения и различия между множествами, что помогает визуализировать логические отношения и выявить общие или уникальные элементы. Диаграмма Венна активно используется в различных областях, включая математику, логику, статистику, информатику и многие другие.

Основной элемент диаграммы Венна — это круги, каждый из которых представляет одно множество. Круги пересекаются в тех местах, где множества имеют общие элементы. Чем больше пересечение, тем больше общих элементов имеют множества. Также на диаграмме можно использовать прямоугольники и другие геометрические фигуры для представления множеств или их отношений. С помощью диаграммы Венна можно решать разнообразные задачи: определять пересечения, объединения и разность множеств, а также находить значения функций и выражений.

Примером использования диаграммы Венна может служить задача о классификации животных. Допустим, имеется множество животных, которые могут быть млекопитающими, птицами или рыбами. Используя диаграмму Венна, можно наглядно показать, какие животные являются млекопитающими, какие птицами, а какие являются и млекопитающими, и птицами одновременно. Таким образом, диаграмма Венна помогает классифицировать объекты и демонстрирует их сходства и различия.

Однако следует отметить, что диаграмма Венна имеет свои ограничения. Она может быть ограничена только конечным набором множеств, так как количество областей пересечения растет экспоненциально с увеличением количества множеств. Кроме того, диаграмма Венна не всегда может точно отразить все возможные отношения между множествами и может быть сложной для интерпретации в случае большого количества пересечений. Несмотря на это, диаграмма Венна остается эффективным инструментом для визуализации и анализа множественных данных.

Диаграмма Венна: определение, примеры, особенности

Диаграмма Венна представляет собой графическое представление множеств и их отношений между собой. Это инструмент, который используется в математике, логике, статистике, информатике и других областях, чтобы показать пересечения и различия между множествами.

Основными элементами диаграммы Венна являются окружности, которые представляют множества или группы элементов. Области пересечения между окружностями показывают элементы, принадлежащие нескольким множествам одновременно.

Диаграмма Венна может быть использована для решения различных задач. Она может помочь визуализировать логические отношения между множествами, определить взаимное исключение и пересечение элементов, а также выявить общие и уникальные элементы в нескольких множествах.

Примеры применения диаграммы Венна включают анализ данных, классификацию объектов, организацию информации и решение логических задач. Например, диаграмма Венна может быть использована для понимания отношений между различными видами животных (млекопитающие, птицы, рептилии) или для определения, какие продукты питания являются источниками белка, углеводов и жиров.

Важно отметить, что диаграмма Венна не является единственным инструментом для анализа множеств. Она имеет свои ограничения и может быть неприменима в случае большого количества множеств или сложных отношений между ними. Однако, при правильном использовании диаграмма Венна является полезным инструментом для визуализации и анализа множеств и их отношений.

Видео по теме:

Что такое диаграмма Венна?

Основная идея диаграммы Венна заключается в использовании окружностей или эллипсов для обозначения множеств, а пересечения множеств — для обозначения совместных элементов. Благодаря своей простоте и понятности, диаграммы Венна широко применяются в математике, логике, статистике, биологии, информатике и других науках.

Примеры использования диаграммы Венна:

• В математике диаграммы Венна используются для иллюстрации операций над множествами, таких как объединение, пересечение и разность.
• В статистике диаграммы Венна активно применяются для визуализации данных, связанных с сопоставлением и группировкой информации.
• В биологии диаграммы Венна помогают показать сходства и различия между разными видами организмов или между генетическими группами.

Диаграммы Венна обладают выразительностью и позволяют легко сравнивать множества и анализировать их отношения. Они могут быть использованы для решения задач, связанных с классификацией, пересечением и объединением групп элементов.

Примеры использования диаграммы Венна в математике

Вот несколько примеров использования диаграммы Венна в математике:

1. Множества чисел

Диаграмма Венна может быть использована для представления различных типов чисел, таких как натуральные числа, целые числа, рациональные числа и действительные числа. На диаграмме каждое множество будет представлено кругом, а пересечения между кругами будут показывать общие элементы между различными типами чисел.

2. Логические операции

Диаграмма Венна может быть использована для визуализации различных логических операций, таких как объединение, пересечение и разность множеств. На диаграмме каждое множество будет представлено кругом, а пересечения и разности между кругами будут показывать результаты логических операций.

3. Вероятность и статистика

Диаграмма Венна может быть использована для визуализации вероятностей и статистических данных. На диаграмме каждое множество будет представлено кругом, а пересечения между кругами будут показывать вероятности событий или соотношение различных категорий данных.

4. Алгебраические структуры

Диаграмма Венна может быть использована для представления алгебраических структур, таких как группы, кольца и поля. На диаграмме каждое множество будет представлено кругом, а пересечения и разности между кругами будут показывать связи и свойства элементов алгебраической структуры.

Это только некоторые примеры использования диаграммы Венна в математике. Она может быть применена во многих других областях, чтобы визуально представить и анализировать сложные связи и отношения между множествами и объектами.

Вопрос-ответ:

Что такое диаграмма Венна?

Диаграмма Венна — это графический метод представления множеств и их отношений друг к другу. Она состоит из нескольких пересекающихся окружностей или эллипсов, каждый из которых представляет отдельное множество, а пересечение окружностей показывает общие элементы между множествами.

Как использовать диаграмму Венна для нахождения пересечения множеств?

Для нахождения пересечения множеств на диаграмме Венна необходимо обратить внимание на область пересечения окружностей или эллипсов, которые представляют данные множества. Общие элементы будут находиться в этой области пересечения.

Какие примеры можно привести для диаграмм Венна?

Примерами использования диаграмм Венна могут быть следующие ситуации: показать пересечение множеств мужчин и котов (некоторые мужчины могут быть владельцами кошек), отобразить совокупность студентов, занимающихся математикой и физикой (некоторые студенты могут заниматься обоими предметами) и т.д.

В чем особенности использования диаграмм Венна в математике?

Диаграммы Венна могут быть полезным инструментом для визуализации отношений между множествами в математике. Они помогают лучше понять пересечение множеств, различать общие и различные элементы, а также проводить операции с множествами, такие как объединение и разность.

Можно ли использовать диаграммы Венна для более чем трех множеств?

Да, диаграммы Венна могут быть использованы для отображения отношений между более чем трех множеств. Для этого можно использовать более сложные комбинации пересекающихся окружностей или эллипсов, чтобы показать общие и различные элементы между множествами.

Что такое диаграмма Венна?

Диаграмма Венна — это графическое представление множества и их взаимосвязей. Она состоит из нескольких пересекающихся кругов, каждый из которых представляет отдельное множество, а пересечение кругов — общие элементы множеств.

Диаграмма Венна в логике и множествах

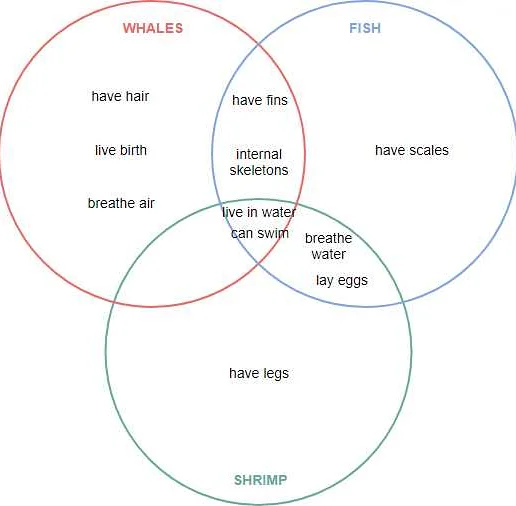
В логике диаграмма Венна используется для визуализации отношений между логическими выражениями и операциями над ними. На диаграмме Венна логические выражения представляются в виде окружностей или эллипсов, а отношения между ними – в виде пересекающихся или непересекающихся областей.

В математической логике диаграмма Венна часто используется для иллюстрации операций над множествами, таких как объединение, пересечение и разность. Каждое множество представляется в виде окружности или эллипса, а операции – в виде пересечений и объединений областей.

Диаграмма Венна позволяет наглядно представить логические связи и отношения между множествами, что упрощает понимание и анализ сложных логических выражений. Она также может использоваться для решения задач по теории множеств и логике, а также в других областях математики и информатики.

Особенности диаграммы Венна в математике

Основная особенность диаграммы Венна заключается в том, что она позволяет наглядно и наглядно представить пересечение и объединение множеств, а также различные операции, такие как дополнение, разность и симметрическая разность множеств.

Диаграмма Венна представляет собой эллипсы или окружности, которые пересекаются и перекрываются друг с другом. Каждое множество представляется своим собственным эллипсом или окружностью, а пересечения образуют общие области, которые показывают элементы, принадлежащие двум или более множествам.

В диаграмме Венна элементы множества обозначаются точками, которые располагаются внутри соответствующего эллипса или окружности. Если элемент принадлежит только одному множеству, то он находится внутри этого множества. Если элемент принадлежит нескольким множествам, то он находится в пересечении этих множеств.

Диаграмма Венна также позволяет наглядно отобразить логические операции над множествами. Например, объединение двух множеств представляется как общая область, которая содержит все элементы обоих множеств. А дополнение множества отображается как область, которая содержит все элементы, не принадлежащие данному множеству.

Одна из особенностей диаграммы Венна – ее гибкость и простота использования. Она позволяет представлять сложные логические операции и отношения между множествами в понятном и наглядном виде. Кроме того, диаграмма Венна может быть использована для решения различных задач, таких как нахождение пересечения и разности множеств, анализ логических выражений и решение задач по теории множеств.

В заключение, диаграмма Венна является важным инструментом в математике, который позволяет наглядно представлять и анализировать множества и их взаимосвязи. Она помогает разобраться в сложных логических операциях и решить различные задачи, связанные с теорией множеств.

Сравнение диаграммы Венна с другими методами визуализации данных

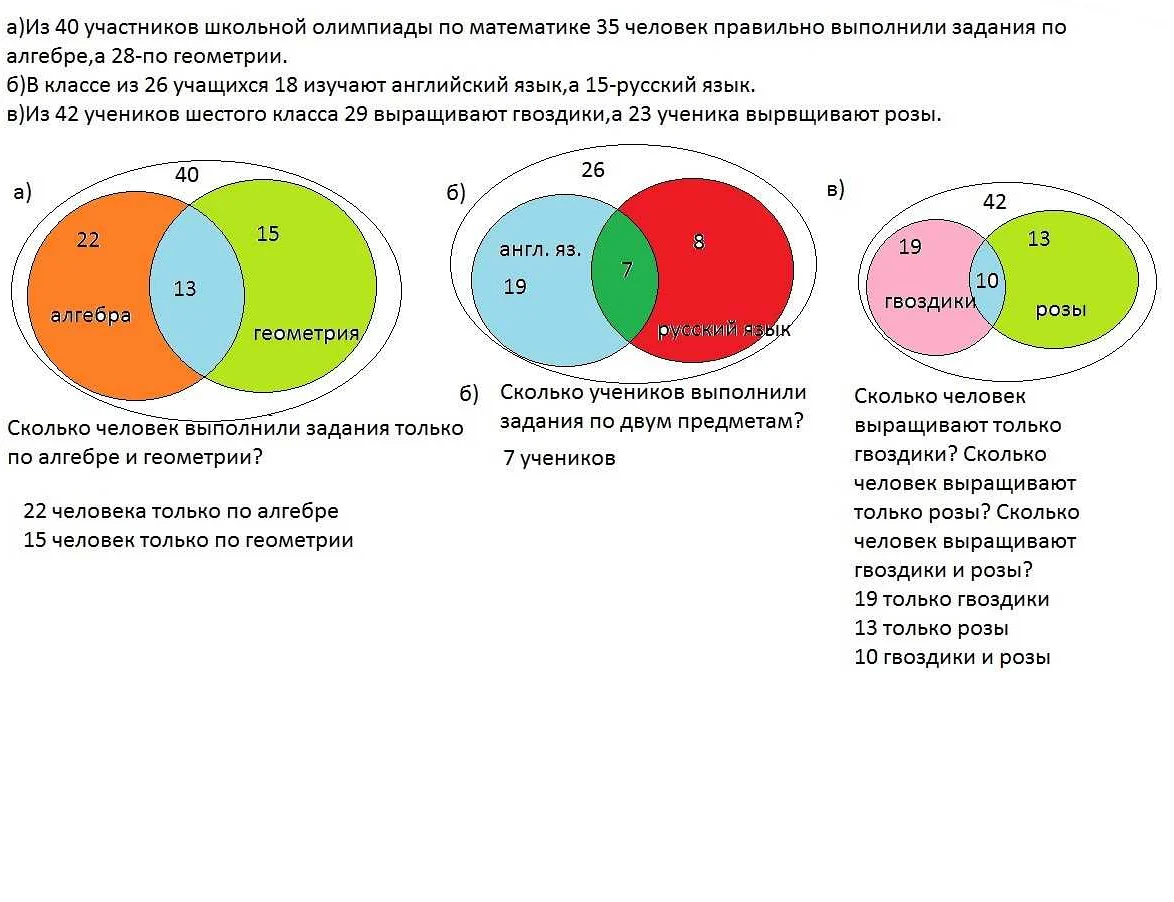
Один из таких методов — гистограмма. Гистограмма представляет собой столбчатую диаграмму, в которой каждому значению переменной соответствует столбец. Гистограмма позволяет наглядно представить распределение данных и выявить основные характеристики выборки, такие как среднее значение и стандартное отклонение.

Другим популярным методом визуализации данных является круговая диаграмма. Круговая диаграмма представляет собой круг, разделенный на секторы, каждый из которых соответствует определенной категории. Размер сектора пропорционален значению, которое он представляет. Круговая диаграмма позволяет наглядно сравнивать доли различных категорий и выявлять их относительные величины.

Также стоит упомянуть линейные графики, которые используются для отображения изменения переменной во времени или в зависимости от другой переменной. Линейный график представляет собой граф, на котором значения переменной отображаются в виде точек, соединенных линией. Линейные графики позволяют наглядно показать тренды и закономерности в данных.

Все эти методы визуализации данных имеют свои особенности и применяются в различных ситуациях. Диаграмма Венна особенно полезна для выявления пересечений и взаимосвязей между наборами данных. Однако при выборе метода визуализации данных необходимо учитывать особенности данных, а также цели и задачи исследования.

Как создать диаграмму Венна в математике?

Для создания диаграммы Венна в математике нужно следовать определенным шагам:

1. Определите множества, которые хотите сравнить и изобразить в диаграмме. Обычно это два или более множества с пересекающимися или непересекающимися элементами.
2. Нарисуйте круги, представляющие каждое множество. Размер и позиция кругов могут быть произвольными, но обычно они пересекаются или содержат друг друга.
3. Разместите элементы каждого множества внутри соответствующего круга. Если элемент принадлежит нескольким множествам, разместите его в пересечении кругов.
4. Подпишите круги, указав названия соответствующих множеств. Также можно добавить подписи к элементам внутри кругов, чтобы уточнить их значения.

Создание диаграммы Венна в математике помогает наглядно представить отношения между множествами и их элементами. Это полезный инструмент для изучения и анализа различных математических концепций, таких как теория множеств, логика и вероятность.

Возможности применения диаграммы Венна в математике

В математике диаграмма Венна может быть использована для:

1. Иллюстрации логических операций:

С помощью диаграммы Венна можно визуализировать операции пересечения, объединения и разности между множествами. Например, если есть два множества A и B, то пересечение множеств будет представлено областью пересечения двух окружностей, объединение — объединением окружностей, а разность — разностью окружностей.

2. Решения задач на комбинаторику:

В комбинаторике диаграмма Венна может быть использована для решения задач на пересечение множеств. Например, можно наглядно представить ситуацию, когда нужно найти количество элементов, принадлежащих одновременно двум или более множествам.

3. Построения диаграмм Эйлера:

Диаграмма Венна может быть использована для построения диаграмм Эйлера, которые позволяют визуализировать отношения между множествами и подмножествами. Например, можно построить диаграмму Эйлера для семейства множеств A, B и C, чтобы увидеть отношения между ними и выделить области, где находятся только определенные элементы.

В заключение, диаграмма Венна является удобным инструментом для визуализации логических отношений и операций между множествами в математике. Она помогает лучше понять связи между элементами и упрощает решение задач, связанных с комбинаторикой и логикой.