Что такое дифференциал математика

Дифференциал в математике — это понятие, используемое для изучения изменений функций. Он позволяет определить, как величина функции меняется при изменении ее аргумента. Дифференциал является основным инструментом дифференциального исчисления и широко применяется в различных областях науки и техники. Узнайте больше о дифференциале и его применении в математике.

Дифференциал – одно из важнейших понятий математического анализа, которое имеет широкое применение в различных областях науки и техники. Дифференциальное исчисление является одной из основных ветвей математики и позволяет исследовать поведение функций и их производных в окрестности заданной точки.

Понятие дифференциала основывается на идеи локального линейного приближения функции. Дифференциал функции f(x) в точке x=a представляет собой приращение функции в окрестности точки a, которое можно выразить через приращение аргумента. Дифференциал обычно обозначается как dx и показывает, насколько изменится значение функции при малом изменении аргумента.

Дифференцирование функций – это процесс нахождения производной функции. Производная функции показывает скорость изменения функции в зависимости от значения аргумента. При нахождении производной используется понятие дифференциала и основные правила дифференцирования, такие как правило суммы, правило произведения, правило цепочки и другие.

Дифференциал имеет широкое применение в различных областях науки, таких как физика, экономика, биология и многие другие. Он позволяет решать разнообразные задачи, связанные с оптимизацией процессов, моделированием систем и анализом поведения функций.

Изучение дифференциала и дифференциального исчисления является важной частью математического образования и позволяет развить навыки аналитического мышления и решения задач. Основные принципы дифференцирования, основанные на понятии дифференциала, широко применяются в различных областях науки и техники и являются необходимыми для понимания более сложных математических концепций и методов.

Определение дифференциала и его роль в математике

Формально, дифференциал функции f(x) в точке x определяется как произведение производной функции в данной точке на приращение аргумента:

df(x) = f'(x)dx

где df(x) – дифференциал функции f(x), f'(x) – производная функции f(x) в точке x, dx – приращение аргумента.

Роль дифференциала в математике очень важна. С его помощью можно исследовать свойства функций, находить точки экстремума, а также решать задачи оптимизации и приближенные значения функций.

Дифференциал также используется для построения дифференциальных уравнений, которые являются основой многих разделов математики и физики.

Основные принципы дифференциала в математике включают:

• Линейность: дифференциал суммы двух функций равен сумме дифференциалов этих функций.
• Правило Лейбница: дифференциал произведения функций равен произведению дифференциала одной функции на значение другой функции плюс произведение значения первой функции на дифференциал второй функции.
• Дифференциал функции сложной переменной: для функции f(g(x)) дифференциал равен произведению производной f от g на дифференциал g.

В заключение, дифференциал играет ключевую роль в математике, позволяя анализировать и приближенно описывать функции, а также решать различные задачи оптимизации и моделирования.

Производная функции и связь с дифференциалом

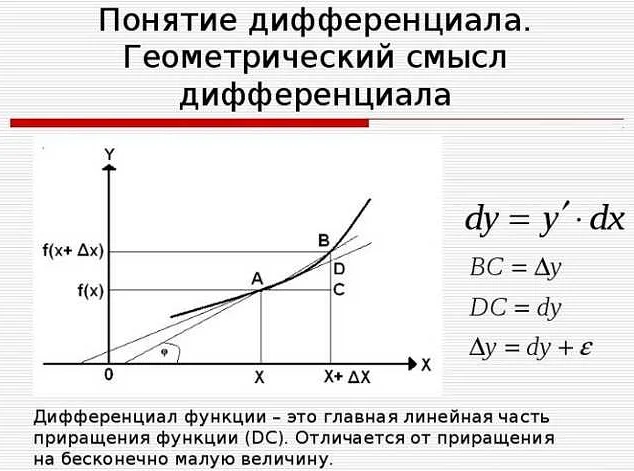
Пусть у нас есть функция f(x), определенная на некотором интервале (a, b). Производная функции f(x) в точке x_0 обозначается f'(x_0) или df/dx|_{x=x_0} и определяется следующим образом:

Определение производной:

f'(x_0) = lim_(h->0) (f(x_0 + h) — f(x_0))/h

То есть, производная функции в точке x_0 равна пределу отношения приращения функции f(x) к приращению аргумента x при стремлении приращения аргумента к нулю.

Связь производной функции с дифференциалом выражается следующим равенством:

Связь производной с дифференциалом:

df = f'(x) * dx

Здесь df – дифференциал функции f(x), dx – приращение аргумента x, а f'(x) – производная функции f(x) в точке x.

Дифференциал позволяет приближенно вычислять изменение функции при малых приращениях аргумента. С помощью производной и дифференциала можно решать задачи оптимизации и находить экстремумы функций, а также анализировать поведение функции в окрестности точки.

Производные и дифференциалы являются важными инструментами в математическом анализе и находят применение в различных областях, таких как физика, экономика и теория вероятностей.

Первообразная функции и ее отношение к дифференциалу

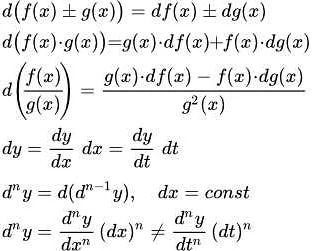
Первообразная функции играет важную роль в теории дифференцирования. Зная производную функции, мы можем найти ее первообразную. Этот процесс называется интегрированием или нахождением неопределенного интеграла.

Отношение между первообразной функции и дифференциалом заключается в том, что дифференциал функции является приращением значения этой функции, а первообразная функции позволяет найти значение функции по ее дифференциалу.

Формально, если F(x) — первообразная функции f(x), то справедливо следующее равенство:

F(x) = ∫ f(x) dx + C

где C — постоянная, называемая постоянной интегрирования. Она возникает в результате того, что при дифференцировании константа исчезает.

Таким образом, первообразная функции и дифференциал тесно связаны между собой: первообразная функции позволяет находить значение функции по ее дифференциалу, а дифференциал является приращением значения функции.

Точка локального экстремума и дифференциал

В математике точка называется локальным экстремумом функции, если она представляет собой максимум или минимум функции в некоторой окрестности этой точки. Локальный экстремум может быть достигнут внутри области определения функции или на её границе.

Дифференциалом функции f(x) называется линейное приближение функции в окрестности точки x. Он позволяет оценить изменение функции при небольших изменениях аргумента. Дифференциал функции обозначается как df(x) или dx и определяется следующим образом:

• Если f(x) дифференцируема в точке x, то df(x) = f'(x) * dx, где f'(x) — производная функции f(x) в точке x, а dx — приращение аргумента.
• Если f(x) не является дифференцируемой в точке x, то df(x) не существует.

В точке локального экстремума производная функции равна нулю или не существует. Это связано с тем, что в такой точке касательная к графику функции является горизонтальной. Дифференциал функции в точке локального экстремума также равен нулю или не существует.

Точка локального экстремума имеет важное значение в оптимизации и экономике. Она позволяет найти наилучшие значения функций в заданной области и принять оптимальные решения.

Дифференциал и линейная аппроксимация функции

Дифференциал функции f(x) в точке x0 обозначается как df(x0) и определяется следующим образом:

df(x0) = f'(x0)·dx,

где f'(x0) – производная функции f(x) в точке x0, а dx – малая приращение переменной x.

Дифференциал является линейной аппроксимацией функции вблизи точки x0. Это означает, что при достаточно малом приращении dx, значение функции f(x) можно приближенно вычислить с помощью формулы:

f(x) ≈ f(x0) + f'(x0)·dx.

Таким образом, дифференциал позволяет заменить функцию сложной формы на линейную функцию, что значительно упрощает проведение вычислений и анализ функции в окрестности заданной точки.

Правила дифференцирования и их применение

Основные правила дифференцирования включают:

ПравилоФункцияПроизводная

Правило линейности	f(x) = ax + b	f'(x) = a
Правило степенной функции	f(x) = x^n	f'(x) = nx^(n-1)
Правило суммы	f(x) = g(x) + h(x)	f'(x) = g'(x) + h'(x)
Правило произведения	f(x) = g(x) * h(x)	f'(x) = g'(x) * h(x) + g(x) * h'(x)
Правило частного	f(x) = g(x) / h(x)	f'(x) = (g'(x) * h(x) — g(x) * h'(x)) / h(x)^2

Эти правила могут быть комбинированы и применены для нахождения производной сложных функций. Например, если функция представлена как композиция двух функций f(g(x)), то можно использовать правило цепочки для вычисления производной.

Применение правил дифференцирования позволяет находить касательные и нормали к графикам функций, определять точки экстремума и изучать поведение функций в различных точках и интервалах. Также дифференцирование используется в задачах оптимизации, моделировании и многих других областях.

Дифференциал и его роль в оптимизации функций

Дифференциал функции обозначается символом dx и показывает, как изменяется значение функции при изменении аргумента на очень малую величину Δx. Дифференциал функции может быть записан как произведение производной функции и приращения аргумента: dx = f'(x)Δx.

Роль дифференциала в оптимизации функций заключается в том, что он позволяет найти экстремумы функций, то есть точки минимума или максимума. Для этого используется необходимое условие экстремума – равенство нулю дифференциала функции. Если дифференциал равен нулю в точке, то это может быть точка экстремума.

Дифференциал также используется для нахождения касательной к графику функции в заданной точке. Касательная показывает направление наиболее быстрого изменения функции в этой точке и часто используется в оптимизации для поиска оптимальных значений функций.

В заключение, дифференциал играет важную роль в оптимизации функций, помогая находить экстремумы и оптимальные значения функций. Он позволяет анализировать изменения функции вблизи каждой точки и строить линейные приближения, что является основой для оптимизационных методов в математике и других науках.

Дифференциал и его применение в физике и экономике

В физике дифференциал используется для описания изменений физических величин. Например, когда мы говорим о скорости изменения расстояния с течением времени, мы используем понятие дифференциала. Дифференциал также используется для апроксимации сложных функций и решения дифференциальных уравнений.

В экономике дифференциал используется для описания изменений величин, связанных с экономическими процессами. Например, дифференциал может быть использован для изучения изменения производства товаров относительно изменения затрат. Он также может использоваться для анализа изменения спроса на товары при изменении цен.

В обоих случаях, как в физике, так и в экономике, дифференциал позволяет нам анализировать и описывать изменения величин с использованием математических методов.

Вопрос-ответ:

Что такое дифференциал в математике?

В математике дифференциал – это понятие, используемое в теории дифференциальных уравнений и математическом анализе. Дифференциал определяется как приращение функции при бесконечно малом изменении аргумента.

Какие основные принципы дифференциала?

Основные принципы дифференциала включают в себя аддитивность, линейность, мультипликативность и сохранение порядка.

Как применяется дифференциал в теории дифференциальных уравнений?

В теории дифференциальных уравнений дифференциал используется для решения уравнений, которые описывают зависимость между функцией и ее производными. Дифференциал позволяет найти приращение функции при изменении ее аргумента.

Какую роль играет дифференциал в математическом анализе?

В математическом анализе дифференциал играет основную роль при нахождении производной функции. Дифференциал позволяет определить, как меняется функция при изменении аргумента в окрестности заданной точки.

Можно ли сказать, что дифференциал является бесконечно малой величиной?

Да, дифференциал можно рассматривать как бесконечно малую величину. Он представляет собой приращение функции при бесконечно малом изменении аргумента.

Видео по теме: