Кто придумал производную в математике
Содержимое
- 1 Кто придумал производную в математике
- 1.1 История происхождения производной в математике
- 1.2 Появление идеи производной
- 1.3 Первые шаги в развитии производной
- 1.4 Вклад Лейбница в развитие производной
- 1.5 Открытие формулы дифференцирования
- 1.6 Применение производной в физике
- 1.7 Развитие теории дифференцирования в XIX веке
- 1.8 Создание математического аппарата дифференциального исчисления
- 1.9 Современное применение производной в науке и технике
- 1.10 Вопрос-ответ:
- 1.10.0.1 Кто придумал производную в математике?
- 1.10.0.2 Как развивалась идея производной в математике?
- 1.10.0.3 Какое значение имеет производная в математике?
- 1.10.0.4 Какие методы используются для нахождения производной?
- 1.10.0.5 В каких областях математики и физики применяется производная?
- 1.10.0.6 Кто придумал производную в математике?
- 1.11 Видео по теме:
Узнайте о том, кто является изобретателем производной в математике, и какие открытия и идеи привели к ее созданию. Исследуйте важные вклады некоторых великих математиков в развитие этого фундаментального понятия и его применение в различных областях науки и инженерии.
Одной из фундаментальных концепций математики является производная. Это понятие, которое позволяет изучать изменение функции, ее скорость и направление. Производная имеет широкое применение в различных областях науки и техники.
История происхождения производной начинается в XVII веке. Одним из первых, кто занимался исследованием этого понятия, был английский математик Исаак Ньютон. В своей работе «Методы» он впервые ввел понятие производной и разработал основы дифференциального исчисления. Ньютон использовал символы «dot» и «prime» для обозначения производной.
Одновременно с Ньютоном над развитием производной работал и немецкий математик Готфрид Лейбниц. В своих трудах Лейбниц использовал символ дифференциала «d» для обозначения производной. Он также ввел понятие интеграла и разработал методы интегрирования.
Впоследствии производная и интеграл стали ключевыми понятиями математического анализа и играют важную роль во многих областях науки и техники.
По мере развития математики производная стала объектом более глубокого исследования. В XIX веке математики Эйлер, Лагранж, Коши и другие внесли значительный вклад в теорию производной. Они разработали формальные определения, методы вычисления и теоремы о производной. Также они применяли производную для решения задач из физики, механики и других научных областей.
В XX веке исследования в области производной продолжились. Появилось понятие обобщенной производной, которое позволяет работать с функциями, не являющимися классически дифференцируемыми. Кроме того, производная нашла свое применение во многих прикладных областях, таких как финансовая математика, оптимизация и машинное обучение.
История происхождения производной в математике
История происхождения производной в математике начинается с появления идеи о скорости изменения функции в заданной точке. В древности античные математики, такие как Архимед и Евклид, использовали концепцию скорости для решения геометрических задач. Однако, именно Ньютон и Лейбниц впервые формализовали понятие производной и разработали математический аппарат для ее вычисления.
Исследования Ньютона и Лейбница в области математического анализа привели к появлению дифференциального и интегрального исчисления. В своих работах Ньютон и Лейбниц использовали понятие предела, чтобы определить производную функции. Они показали, что производная функции является мгновенной скоростью изменения этой функции в заданной точке.
В дальнейшем идея производной была развита и уточнена другими математиками, такими как Эйлер, Коши и Вейерштрасс. Они установили строгие определения производной и разработали математический аппарат для ее вычисления. Эти разработки позволили математикам применять производные для решения различных задач и исследования функций.
С появлением компьютеров и развитием численных методов вычисления производной, математики получили новые возможности для исследования функций и решения задач. Сегодня производная является одним из основных понятий математического анализа и широко применяется в различных областях науки и техники.
Таким образом, история происхождения производной в математике связана с развитием идеи о скорости изменения функции и ее формализацией Ньютоном и Лейбницем. Дальнейшие разработки математиков позволили установить строгое определение производной и разработать методы ее вычисления.
Появление идеи производной
Концепция производной в математике возникла в XVII веке. Одним из первых математиков, который начал исследовать понятие производной, был английский математик Исаак Ньютон. Он разработал методы дифференцирования, которые позволяли находить производные функций.
Ньютон использовал аппроксимацию для определения производной. Он предполагал, что если функция непрерывна, то она может быть приближена с помощью касательной к графику функции в данной точке. Идея заключалась в том, что приближенный наклон касательной в данной точке является производной функции в этой точке.
Однако Ньютон не формализовал понятие производной и не предложил единый математический формат для ее вычисления. Эту работу продолжало развивать другое математическое поколение, в частности, Лейбниц и Эйлер.
Важно отметить, что идея производной возникла из необходимости решать проблемы, связанные с движением и изменением величин. Математики поняли, что производная может быть использована для определения скорости изменения функции в определенной точке и для нахождения экстремумов функции.
Таким образом, понятие производной является фундаментальным в математике и имеет широкое применение во многих областях науки и техники.
Первые шаги в развитии производной

Развитие производной в математике началось в XVII веке. Одним из первых математиков, изучавших производную, был английский ученый Айзек Ньютон. В своих работах Ньютон использовал представление производной как предела отношения изменения функции к изменению ее аргумента.
Одновременно с Ньютоном, независимо друг от друга, производную начал изучать и немецкий ученый Готфрид Лейбниц. Лейбниц ввел символ дифференциала, обозначаемый как d, и представил производную в виде отношения дифференциала функции к дифференциалу ее аргумента.
Первые шаги в развитии производной позволили математикам решать сложные задачи, связанные с нахождением касательных кривых, определением экстремумов функций и т. д. Впоследствии производная стала одним из основных понятий математического анализа и нашла широкое применение в различных областях науки и техники.
Вклад Лейбница в развитие производной

Готфрид Вильгельм Лейбниц был немецким математиком, философом и логиком, который внес значительный вклад в развитие производной. Лейбниц разработал идею дифференциального исчисления независимо от английского математика Исаака Ньютона.
В своих работах Лейбниц предложил символическое обозначение для производной, которое до сих пор используется в математике. Он использовал символ «d» для обозначения малого изменения и символ «dx» для обозначения бесконечно малого приращения аргумента функции. Таким образом, он ввел понятие дифференциала и дифференцирования.
Лейбниц также разработал правила дифференцирования и формулу для вычисления производной сложной функции, которая была названа «правилом Лейбница». Это правило позволяет находить производную сложной функции в терминах производных ее составляющих функций.
Важным достижением Лейбница было введение понятия интеграла, которое является обратной операцией к дифференцированию. Он также разработал методы вычисления определенных интегралов и формулу для вычисления площади под кривой.
Благодаря своим открытиям и разработкам, Лейбниц сыграл важную роль в развитии и популяризации производной и дифференциального исчисления. Его работы стали основой для дальнейшего развития математики и нашли применение во многих областях науки и техники.
Открытие формулы дифференцирования
Одним из первых математиков, который занимался исследованием производных функций, был Исаак Ньютон. В своих работах он вывел основные правила дифференцирования, включая формулу для нахождения производной степенной функции. Это открытие положило основу для дальнейшего развития теории производных.
Важную роль в развитии формулы дифференцирования сыграл Леонард Эйлер. Он ввел понятие бесконечно малой величины и разработал алгебраические методы дифференцирования, включая формулу дифференцирования сложной функции. Эйлер также сформулировал основные правила дифференцирования, которые обобщили и расширили представления о производных функций.
Вторая половина XIX века стала переломным моментом в развитии формулы дифференцирования. В этот период великую роль сыграли математики Александр Коши и Карл Вейерштрасс. Коши установил теорему о среднем значении, которая является основой для формулы Лагранжа и других формул дифференцирования. Вейерштрасс же разработал всеобщие методы дифференцирования и доказал теорему о пределе функции, которая является основой для формулы Коши и других формул дифференцирования.
Современная формула дифференцирования, которая используется в математическом анализе, была получена в результате синтеза работ всех ученых, которые занимались этой проблемой. Она позволяет находить производные различных функций и применяется во многих областях науки и техники.
Открытие формулы дифференцирования является важным этапом в истории математики и открывает двери для новых открытий и развития других математических теорий. Благодаря работам ученых, которые занимались этой проблемой, математика приобрела новые инструменты и возможности для анализа и понимания различных явлений в науке и жизни.
Применение производной в физике

В физике производная используется для решения задач, связанных с изменением физических величин в зависимости от времени. Она позволяет определить скорость изменения величины и понять, как она влияет на поведение системы.
Применение производной в физике проявляется во множестве случаев. Например, при решении задач о движении тела, производная используется для определения скорости и ускорения тела. Она позволяет рассчитать траекторию движения, прогнозировать будущее положение объекта и анализировать его поведение.
Производная также применяется в задачах, связанных с электрическими и магнитными полями. Она помогает определить изменение электрического и магнитного потенциала в пространстве, рассчитать силу электрического поля или магнитного поля, а также описать их взаимодействие с другими телами.
Благодаря применению производной, физики могут более точно описывать и предсказывать различные физические явления и процессы. Она позволяет решать сложные задачи, связанные с изменением величин во времени, и анализировать поведение системы в различных условиях.
Развитие теории дифференцирования в XIX веке

В XIX веке теория дифференцирования претерпела значительное развитие благодаря работам таких математиков, как Карл Густав Якоб Якоби, Карл Вильгельм Фридрих Гаусс и Адриен Мари Лежандр.
Одним из важных шагов в развитии теории дифференцирования была формализация определения производной. Карл Густав Якоби ввел понятие производной функции и разработал методы ее определения. Он ввел символ «d» для обозначения дифференциала и предложил использовать его для записи производной функции. Это стало основой для дальнейшего развития теории дифференцирования.
Карл Вильгельм Фридрих Гаусс также внес значительный вклад в развитие теории дифференцирования. Он разработал теорию комплексного анализа, которая стала основой для решения задач дифференцирования функций комплексного переменного. Его работы открыли новые горизонты в теории дифференцирования и привнесли новые методы и подходы.
Адриен Мари Лежандры внес существенный вклад в развитие теории дифференцирования, особенно в области дифференциальных уравнений. Он разработал теорию дифференциальных уравнений высших порядков и предложил методы их решения. Его работы стали основой для дальнейшего развития дифференциальных уравнений и дифференцирования в целом.
МатематикВклад в развитие дифференцирования
| Карл Густав Якоби | Введение понятия производной функции и разработка методов ее определения. |
| Карл Вильгельм Фридрих Гаусс | Разработка теории комплексного анализа и применение ее в задачах дифференцирования функций комплексного переменного. |
| Адриен Мари Лежандры | Разработка теории дифференциальных уравнений высших порядков и предложение методов их решения. |
Создание математического аппарата дифференциального исчисления
Истоки дифференциального исчисления уходят в древнюю Грецию, однако его полноценное развитие произошло лишь в XVII-XVIII веках. Основой для создания математического аппарата дифференциального исчисления стала работа таких ученых как Ньютон и Лейбниц. Именно они независимо друг от друга пришли к созданию понятия производной и разработали правила ее вычисления.
Итак, Исаак Ньютон и Готфрид Вильгельм Лейбниц оба заслуживают звания создателей дифференциального исчисления. Ньютон, работая над проблемой движения небесных тел, пришел к выводу о необходимости разработки нового математического аппарата. Он вводил понятие скорости изменения величины и определял ее как предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю.
Лейбниц, занимаясь изучением площади криволинейных фигур, также столкнулся с необходимостью введения новых математических понятий. Он предложил использовать понятие дифференциала для описания бесконечно малых изменений величин. Лейбниц также определил понятие производной и разработал правила дифференцирования функций.
После публикации своих работ, Ньютон и Лейбниц оказались в весьма ожесточенной борьбе за первенство в открытии дифференциального исчисления. Спор между ними продолжался много лет и закончился без ясного победителя. Однако оба ученых внесли огромный вклад в развитие математики и создание математического аппарата дифференциального исчисления.
В ходе дальнейшего развития дифференциального исчисления были созданы более общие понятия, такие как интеграл и обратная функция. Они позволили еще более эффективно применять математический аппарат дифференциального исчисления в различных областях науки и техники.
Сегодня дифференциальное исчисление является незаменимым инструментом в математике и физике, а его создание и развитие было важным этапом в истории математики.
Современное применение производной в науке и технике
Одно из основных применений производной находится в физике. Например, производная позволяет рассчитывать скорость и ускорение тела, определять траектории движения и изучать законы сохранения энергии. В механике производная используется для анализа динамики системы и определения равновесных состояний.
В экономике и финансах производная применяется для определения эластичности спроса и предложения, анализа прибыльности и рыночной структуры. Она также используется для моделирования финансовых рынков и принятия решений в инвестиционной деятельности.
В медицине производная находит применение в анализе функций организма, изучении изменений показателей здоровья, а также моделировании и прогнозировании пациентов. Она помогает определить оптимальные дозировки лекарств и провести эффективное лечение.
В инженерии и технике производная используется для анализа и оптимизации процессов. Она позволяет определить критические точки и максимумы/минимумы функций, а также провести оценку стабильности и надежности систем. Производная также находит применение в электротехнике, оптимизации алгоритмов и разработке новых технологий.
Таким образом, производная является мощным инструментом, который находит применение во многих областях науки и техники. Ее использование позволяет проводить анализ, прогнозирование и оптимизацию процессов, что способствует развитию и совершенствованию различных сфер человеческой жизни.
Вопрос-ответ:
Кто придумал производную в математике?
Производная в математике была придумана несколькими математиками независимо друг от друга. Одним из первых, кто занимался исследованием производной, был английский математик Айрнстоун, который использовал понятие «производная» в своих работах в 1695 году. Позднее, фундаментальную теорию и определения производной разработали Готфрид Вильгельм Лейбниц и Исаак Ньютон в конце XVII века.
Как развивалась идея производной в математике?
Идея производной в математике развивалась последовательно. Сначала в конце XVII века Готфрид Вильгельм Лейбниц и Исаак Ньютон внесли свои вклады, разработав основные определения и теорию производной. Затем, в XVIII и XIX веках, математики, такие как Эйлер, Лагранж, Коши и другие, усовершенствовали и дополнили идеи производной, внесли новые методы рассчета и применения производной в разных областях математики и физики.
Какое значение имеет производная в математике?
Производная играет важную роль в математике. Она используется для нахождения скорости изменения функции, а также для определения экстремумов (минимумов и максимумов) функции. Производная также применяется в физике для определения скорости и ускорения объектов.
Какие методы используются для нахождения производной?
Для нахождения производной могут применяться различные методы. Одним из основных методов является дифференцирование, которое основано на определении производной как предела отношения приращения функции к приращению аргумента. Также существуют правила дифференцирования, которые позволяют находить производные сложных функций, произведений, сумм и других комбинаций функций.
В каких областях математики и физики применяется производная?
Производная применяется во многих областях математики и физики. Она используется в анализе функций, исследовании графиков, решении уравнений, определении экстремумов функций и т.д. Кроме того, производная широко применяется в физике для анализа движения тел, определения скорости и ускорения, решении задач динамики и других физических задач.
Кто придумал производную в математике?
История происхождения производной в математике включает в себя вклад многих ученых. Однако, обычно говорят, что основателем теории производной является немецкий математик Готфрид Вильгельм Лейбниц. Он разработал первые основные принципы дифференциального исчисления в конце XVII века.

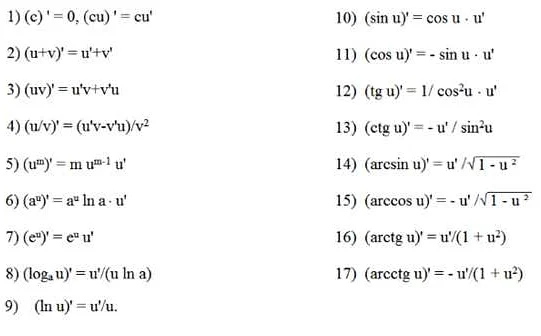


Статья прекрасно описывает историю происхождения производной в математике. Очень интересно узнать, что идея производной возникла у древнегреческих математиков, а затем была развита и формализована Ньютоном и Лейбницем. Они создали основы дифференциального исчисления, которые сейчас широко применяются во многих областях науки и техники. Кстати, статья рассказывает и о женщине-математике Эмили Ноэтер, которая внесла значительный вклад в развитие теории производной. Я узнал много нового об этой удивительной области математики, спасибо автору!
Очень интересная статья! Я всегда задавалась вопросом, как возникла производная в математике. Оказывается, история этого понятия весьма увлекательна. В статье очень подробно описаны трудности, с которыми сталкивались математики в процессе развития производной. Не могу не упомянуть великого математика Лейбница, который внес огромный вклад в развитие этой области. Я удивлена, какие сложные формулы и методы использовались в прошлом для нахождения производных. Это действительно великое достижение человечества. Спасибо автору за такую интересную историческую подборку! Теперь я понимаю, насколько важна производная в современной математике и ее приложениях.
Отличная статья! Я всегда интересовалась историей математики, и она помогает мне лучше понять эту науку. История происхождения производной в математике – это увлекательный путешествие во времени. Первоначально, конечно, это были геометрические исследования античных математиков, таких как Архимед и Евклид. Но само понятие производной возникло только в XVII веке благодаря работе Исааку Ньютону и Готфриду Лейбницу. Они независимо друг от друга разработали математический аппарат, который позволил находить производные для любых функций. Это был настоящий прорыв! В дальнейшем, производная стала важным инструментом в математике, физике и других науках. Производные помогают нам понимать скорость изменения величин и решать сложные задачи. Очень интересно узнать, как эта идея развивалась и применялась в течение времени. Спасибо за такую полезную информацию!