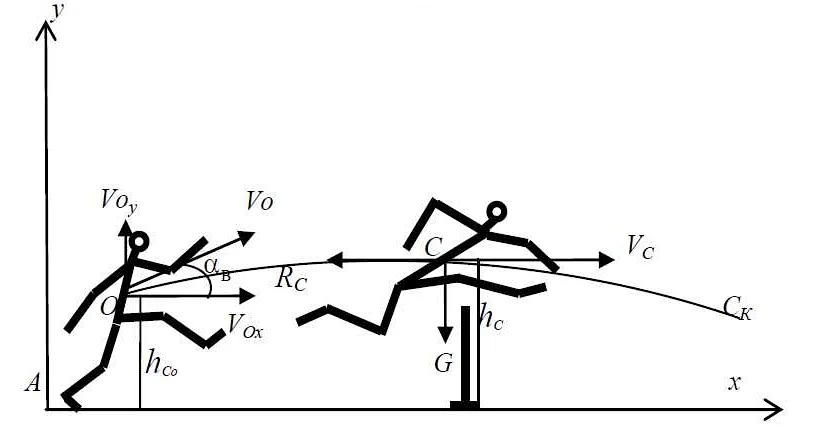
Физические математические модели: что это такое и как они применяются в различных областях

Физические математические модели являются инструментом математического описания физических явлений, а также помогают предсказывать и анализировать результаты экспериментов и исследований. Узнайте подробнее об этом методе в нашей статье.

Физические математические модели — это математические описания физических явлений и процессов в виде уравнений и графиков. Они позволяют проводить исследования и прогнозировать поведение систем в различных условиях.

Примеры физических математических моделей можно привести из разных областей науки: механики, физики твердого тела, электродинамики, квантовой механики, климатологии, биологии и многих других. Модели могут быть дискретными или непрерывными, статическими или динамическими, линейными или нелинейными.

Области применения физических математических моделей также широки: от прогнозирования погоды до разработки электроники, от изучения биологических систем до создания новых материалов. Моделирование также используется в финансовой сфере, чтобы прогнозировать поведение рынков и риски инвестиций.

Важность физических математических моделей состоит в том, что они позволяют представить сложные физические процессы в удобном виде, что позволяет проводить их анализ, оптимизацию и совершенствование в различных областях. Без использования моделей мы не смогли бы достичь многих достижений в науке и технологии, которые имеем сегодня.

Что такое физические математические модели?

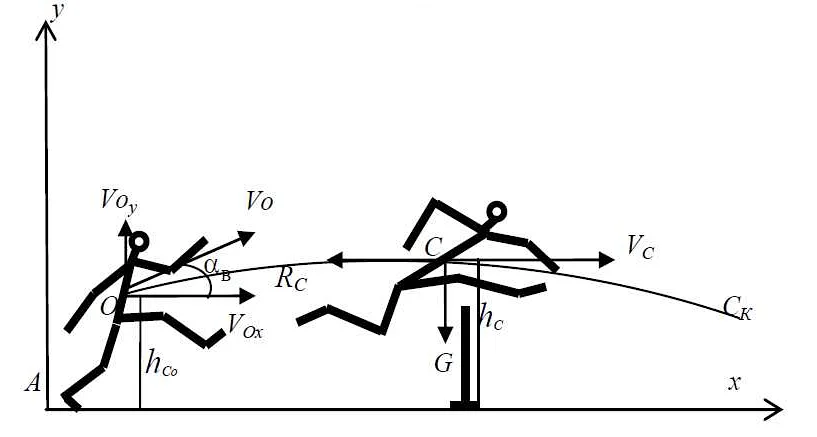
Физические математические модели – это математические описания физических процессов и явлений в природе. Их создание основано на фундаментальных законах физики и математики и используется для предсказания поведения системы при определенных условиях.

Физические математические модели зародились еще в древности, но истинный прорыв в их использовании произошел с появлением компьютеров в 20 веке, которые значительно ускорили процесс вычислений и позволили создавать более сложные модели.

Примерами физических математических моделей могут служить расчеты движения планет, прогноз погоды, симуляторы автомобильных и авиационных движений, а также моделирование роста популяции и многое другое.

Области применения физических математических моделей очень широки. Они используются во многих науках, таких как физика, химия, биология, экономика и др. Также они находят применение в различных инженерных областях, включая проектирование и оптимизацию систем воздушного и судового транспорта, энергетику и другие инженерные дисциплины.

История развития физических математических моделей

Основания физических математических моделей были заложены в Древней Греции. Пифагор, один из основоположников математики, считал, что мир можно описать исключительно математическими закономерностями.

В Средние века в Европе возрождалось научное мышление, и физические математические модели стали более популярны. Одним из первых ученых, который использовал математику для описания мира, был Галилео Галилей. Он предложил закон свободного падения тел и изучал движение тел, взаимодействующих под действием гравитации.

В XVIII веке физические математические модели стали еще более сложными. Исследователи начали использовать методы дифференциальных уравнений для описания движения тел и более точной формулировки законов физики.

В XIX веке, с развитием электричества и магнетизма, физические математические модели стали играть ключевую роль в развитии технологии. Математические модели использовались для проектирования электрических цепей, телекоммуникаций и других технологий.

В наше время физические математические модели используются во многих областях, включая физику, инженерию, медицину, экономику и другие. Современные математические методы позволяют более точно описывать и предсказывать поведение тел и систем, а также разрабатывать более эффективные технологии и строить более точные модели мира.

Функции физических математических моделей

Физические математические модели используются для описания физических процессов в природе, технике и науке. Функции физических математических моделей обладают рядом свойств, которые позволяют получать качественные физические предсказания и прогнозы.

• Описательная функция. Физическая математическая модель должна содержать описательную функцию, которая описывает физический процесс в форме математического уравнения или системы уравнений.
• Прогностическая функция. Физическая математическая модель должна содержать прогностическую функцию, которая позволяет делать прогнозы поведения системы в будущем на основании известных начальных условий.
• Калибровочная функция. Физическая математическая модель должна содержать калибровочную функцию, которая позволяет подобрать значения параметров модели таким образом, чтобы описать физический процесс максимально точно.
• Валидационная функция. Физическая математическая модель должна содержать валидационную функцию, которая позволяет проверять точность моделирования на основе экспериментальных данных.

Функции физических математических моделей играют важную роль в практическом применении моделей. Они позволяют проводить исследования, делать прогнозы, находить оптимальные решения задач, моделировать различные процессы в науке, инженерии и других областях знаний.

Примеры физических математических моделей в химии

Химические процессы могут быть достаточно сложными и непредсказуемыми. Физические математические модели в химии помогают упростить и оптимизировать эти процессы, что является важным фактором в многих областях, таких как производство лекарств, катализ и экология.

Один из примеров физических математических моделей в химии — это модель диффузии. Она позволяет описать перемещение молекул в жидкой или газообразной среде. Такая модель может быть полезной для определения скорости диффузии определенного вещества во время химической реакции. Модель диффузии также может применяться для определения скорости распространения загрязнений в земле или воде.

Еще один пример — это модель катализа. Она используется для определения эффективности катализатора при химической реакции. Эта модель может показать, какие условия оптимальны для катализируемой реакции, такие как температура, давление и состав реакционной смеси.

Другой пример — это модель физико-химической очистки воды. Она используется для определения оптимальных условий для очистки воды, такие как время, температура и концентрация реагентов для удаления загрязнений из воды. Модель также может показать, какие виды загрязнений можно удалить, и какие необходимы дополнительные шаги, чтобы очистить воду полностью.

Все эти примеры демонстрируют, как физические математические модели могут помочь химикам и инженерам оптимизировать и усовершенствовать процессы в химической промышленности, экологии и других областях.

Примеры физических математических моделей в физике

Физическая математическая модель является способом описания физических явлений в математических терминах. В физике такие модели широко используются для изучения свойств материи и ее взаимодействия с окружающей средой. Ниже представим несколько примеров физических математических моделей:

1. Модель движения тела под действием силы тяжести: в данной модели установлено соотношение между массой тела, его ускорением и силой тяжести. Это описание позволяет предсказывать дальнейшее движение тела.
2. Модель электромагнитной волны: данная модель описывает распространение электрической и магнитной энергии в пространстве. Она позволяет определить характеристики электромагнитной волны, такие как частота и амплитуда.
3. Модель идеального газа: эта модель представляет собой математическое описание поведения газа при различных условиях. Она используется для расчета параметров газа, таких как давление, объем и температура.

Эти модели используются в различных областях физики, таких как механика, электродинамика и термодинамика. Они помогают предсказывать и объяснять поведение физических систем в различных условиях.

Примеры физических математических моделей в биологии

Биология – наука о живых организмах, и как ни странно, физические математические модели широко используются в этой области. Вот несколько примеров:

• Модель распространения инфекции: используется для предсказания распространения инфекции в популяции и для разработки стратегии борьбы с эпидемией.
• Модель динамики популяций: используется для изучения взаимодействия между видами и предсказания тенденций в развитии популяции.
• Модель фенотипической пластичности: используется для изучения влияния окружающей среды на генетический материал и наличие изменчивости во внешнем виде и свойствах живых организмов.

Кроме того, математические модели используются для изучения биологических систем на микроуровне, таких как молекулярные взаимодействия, механизмы генной экспрессии и белковая динамика.

Биологические системы – это сложные, динамические системы с множеством переменных. Физические математические модели помогают нам лучше понимать эти системы и предсказывать их поведение в различных условиях.

Примеры физических математических моделей в экономике

Модель роста компании

Модель роста компании — это физическая математическая модель, которая помогает прогнозировать возможный рост компании в будущем. Она основана на анализе факторов, таких как привлечение капитала, управление ресурсами и маркетинговые стратегии компании.

Модель стоимости активов

Модель стоимости активов — это физическая математическая модель, которая используется в экономике для оценки стоимости финансовых инструментов. Она основана на принципах теории информации и статистической теории.

Модель спроса и предложения

Модель спроса и предложения — это физическая математическая модель, которая используется в экономике для описания спроса на товары и услуги, а также предложения этих товаров и услуг на рынке. Она основана на законах рынка и экономических принципах.

Модель экономических циклов

Модель экономических циклов — это физическая математическая модель, которая используется в экономике для анализа колебаний экономической активности. Она основана на цикличности экономической жизни и макроэкономических теориях.

Модель риска и доходности

Модель риска и доходности — это физическая математическая модель, которая используется в экономике для анализа рисков и доходности инвестиций. Она основана на принципах теории вероятности и статистики.

Модель портфеля инвестиций

Модель портфеля инвестиций — это физическая математическая модель, которая используется в экономике для определения оптимального портфеля инвестиций. Она основана на принципах теории портфеля и риск-менеджмента.

Примеры физических математических моделей в метеорологии

В метеорологии физические математические модели используются для прогнозирования погоды и исследования атмосферных явлений. Одним из примеров моделей является модель Глобального Климата (Global Climate Model, GCM).

GCM — это модель, которая позволяет прогнозировать изменения климата на планете в зависимости от различных факторов, включая концентрацию парниковых газов в атмосфере, солнечную активность, температуры океанов и другие изменения.

Еще одним примером физической математической модели в метеорологии является модель численного прогноза атмосферы (Numerical Weather Prediction, NWP). Эта модель использует данные с барометров, радаров, спутников и других источников для прогнозирования погоды на определенном участке земной поверхности в течение нескольких дней.

Модель атмосферы Миллер-Хилл (Miller-Hill Atmosphere Model) — еще один пример физической математической модели в метеорологии. Она представляет собой модель вращения идеальной жидкости в атмосфере, которая учитывает изменения давления и температуры за счет горизонтальных ветров.

Каждая из этих моделей позволяет создавать прогнозы погоды, исследовать изменения в климате и анализировать атмосферные явления на различных уровнях.

Области применения физических математических моделей

Физика: Физические математические модели применяются в области физики для описания физических явлений. Например, моделирование движения тела в свободном падении, движения их воды в океане, или моделирование взаимодействия частиц в термоядерной реакции.

Инженерия: Физические математические модели широко применяются в области инженерии, чтобы определить свойства материалов, проектировать и тестировать новые машины, устройства и сооружения. Например, моделирование напряжения и деформации деталей конструкции или моделирование течения жидкости в трубах.

Экономика: Физические математические модели также используются для анализа экономических явлений, таких как напряжение на финансовых рынках или влияние новых технологий на экономический рост. Модели могут помочь оценить риски и принимать решения на основе данных.

Биология: Физические математические модели могут быть применены для анализа биологических явлений, таких как эволюция и развитие популяции, распространение инфекционных заболеваний или изучение определенных патологий. Например, модель Кольца — Вольтерра используется для анализа взаимодействия двух видов в экосистеме.

Основные проблемы при создании физических математических моделей

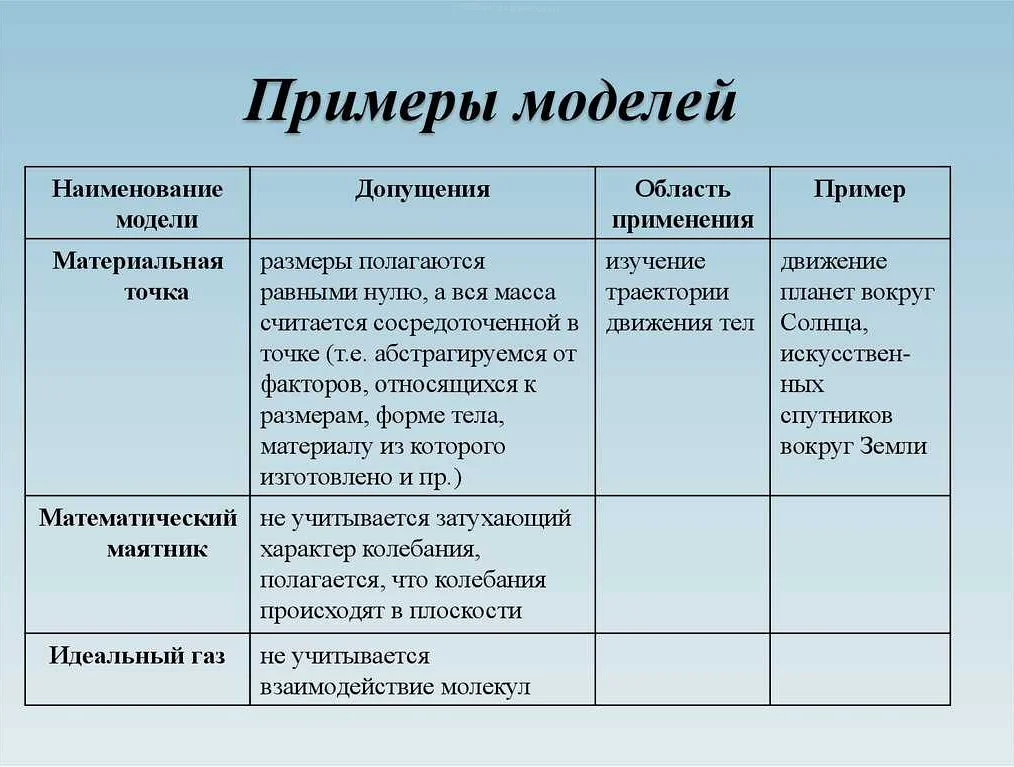
Создание физических математических моделей – сложный и долгий процесс. Один из главных проблем при его осуществлении заключается в том, что между реальным миром и математическим описанием этого мира существуют существенные различия, например, в связи с просчитыванием влияния различных факторов и условий.

Другая проблема, которую приходится решать при создании моделей, – это учет самой природы процесса, который описывается математическую формулой. Математические модели – это лишь приближенное описание реальной ситуации, поэтому для достижения большей точности необходимо учитывать ряд дополнительных условий и факторов.

Также одной из сложностей при создании моделей является их верификация. Для того чтобы убедиться в правильности математического описания, модели часто проверяют на реальных тестовых данных. Однако в случае сложных физических процессов часто бывает трудно найти такие данные, что затрудняет процесс проверки и верификации математической модели.

И наконец, еще одной проблемой при создании моделей является приближенный подход к описанию сложных процессов. При моделировании сложных физических процессов вынуждены принимать упрощенные предположения, что часто приводит к ограничениям и неточностям в итоговых результатах.

Плюсы и минусы применения физических математических моделей в исследованиях

Физические математические модели широко используются в научных и инженерных исследованиях для предсказания поведения сложных объектов и систем. Однако их применение имеет как плюсы, так и минусы.

Плюсы:

• Экономия времени и ресурсов. Физические эксперименты могут быть дорогостоящими и затратными по времени. Использование математических моделей позволяет экономить ресурсы и время, предсказывая результаты экспериментов.
• Удобство варьирования параметров. Физические эксперименты могут быть ограничены возможностями оборудования или масштабом объекта. Математические модели позволяют быстро и легко менять параметры и подходы для изучения объектов различного масштаба.
• Повышение точности предсказания. Физические эксперименты могут быть подвержены ошибкам, например из-за сложности измерения параметров объекта. Математические модели могут повысить точность предсказания путем устранения некоторых факторов неопределенности и погрешности.

Минусы:

• Ограничения точности моделей. Даже самые точные математические модели могут иметь ограничения, особенно в отношении сложных и динамичных систем. Это может приводить к неточным прогнозам и предсказаниям.
• Необходимость верификации моделей. Прежде чем использовать математическую модель для предсказания физического процесса, необходимо убедиться в корректности моделирования. Это может потребовать значительного времени и ресурсов для проверки и верификации модели, что может затруднить процесс исследования.
• Трудности в учете нелинейных зависимостей. Многие физические процессы и системы могут иметь нелинейную зависимость между параметрами, что усложняет создание математических моделей. При этом сами модели могут быть более сложными и требовать большего количества параметров и расчетов.

Таким образом, применение физических математических моделей в исследованиях имеет свои плюсы и минусы, и выбор метода зависит от конкретной задачи и условий исследования.

Вопрос-ответ:

Что такое физические математические модели?

Физические математические модели – это математические выражения, которые описывают поведение физических процессов в природе. Они используются для изучения явлений, которые сложно наблюдать, контролировать или измерить напрямую.

Какие примеры физических математических моделей существуют?

Примеры физических математических моделей могут включать в себя уравнения Ньютона для описания движения тел, уравнения Максвелла для описания электромагнитных полей, уравнение теплопроводности для описания процессов теплопередачи и другие.

В каких областях применяются физические математические модели?

Физические математические модели применяются во многих областях науки и техники, включая физику, математику, инженерное дело, медицину, экономику, аэрокосмическую промышленность и многое другое.

Как создаются физические математические модели?

Физические математические модели создаются на основе сбора данных, экспериментов и наблюдений для определения основных законов и принципов, которые описывают реальные явления. Затем эти законы и принципы формализуются в математические выражения, которые могут быть использованы для прогнозирования поведения системы в различных условиях.

Какие преимущества есть у использования физических математических моделей?

Использование физических математических моделей дает возможность получать прогнозы о поведении системы в различных условиях, без необходимости проводить длительные и дорогостоящие эксперименты. Это может быть полезно в различных областях, включая науку, инженерное дело и промышленность.

Какие типы физических математических моделей существуют?

Существует несколько типов физических математических моделей, включая аналитические модели, численные модели и статистические модели. Аналитические модели – это модели, которые можно решить аналитически, используя математические методы. Численные модели используют численные методы для решения математических моделей. Статистические модели используются для анализа статистических данных и для прогнозирования тенденций.

Какие недостатки есть у использования физических математических моделей?

Недостатки использования физических математических моделей могут включать в себя ограниченность точности модели, необходимость учета всех факторов, которые могут влиять на систему, и сложность разработки и тестирования моделей.

Видео по теме: