Чтобы оценить каков будет период малых колебаний математического маятника используем для вычислений

Для вычисления периода малых колебаний математического маятника применяются специальные формулы и уравнения, которые учитывают длину подвеса и ускорение свободного падения. Узнайте, как оценить период малых колебаний и применить его в практике.

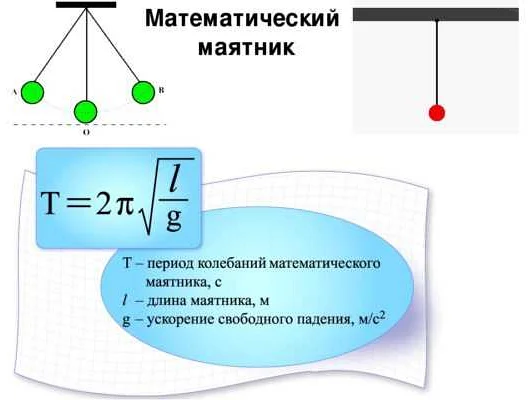
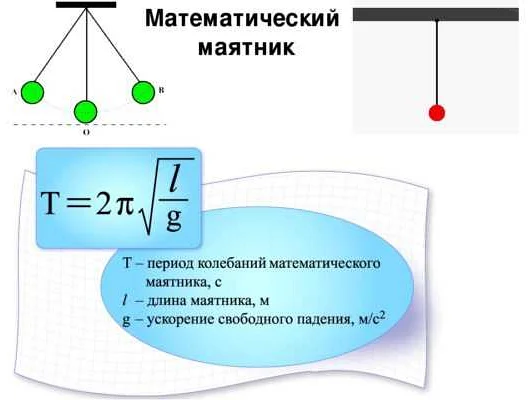
Математический маятник — это система, состоящая из невесомого стержня или нити, на конце которого закреплена материальная точка. Под действием силы тяжести точка начинает колебаться вокруг своего равновесного положения. Период колебаний математического маятника — это временной интервал, за который точка совершает полный оборот в одну сторону и возвращается в исходное положение.

Формула расчета периода малых колебаний математического маятника была впервые выведена Шарлем Булем в 1673 году. Она является одной из основных формул в классической механике и имеет вид:

T = 2π√(L/g)

где T — период колебаний, π — число пи (примерно равно 3,14159), L — длина стержня или нити, на которой закреплена точка, и g — ускорение свободного падения.

В формуле видно, что период колебаний математического маятника зависит от длины стержня или нити и ускорения свободного падения. Чем длиннее стержень или нить, тем больше будет период колебаний. А чем больше ускорение свободного падения, тем меньше будет период колебаний.

Определение и принцип работы математического маятника

Основной закон, описывающий движение математического маятника, называется законом сохранения энергии. Согласно этому закону, в системе математического маятника энергия переходит из потенциальной в кинетическую и обратно, сохраняя свою суммарную величину.

Работа математического маятника основана на силе тяжести, которая действует на тело, закрепленное на стержне или нити. Когда маятник отклоняется от положения равновесия, сила тяжести начинает действовать на него и приводит к его колебаниям. При этом, чем больше отклонение, тем сильнее действует сила тяжести и тем больше будет амплитуда колебаний.

Формула расчета периода малых колебаний математического маятника основана на длине нити (или на расстоянии от точки подвеса до центра масс тела) и на ускорении свободного падения. Она позволяет определить время, за которое маятник совершит одно полное колебание.

Математический маятник находит применение в различных областях, включая физику, математику, инженерию и другие науки. Его принцип работы широко используется в разработке механических устройств, включая метрономы, часы, гиростабилизаторы и многие другие.

Что такое математический маятник и как он функционирует?

Основным принципом работы математического маятника является взаимодействие силы тяжести и упругой силы, возникающей при отклонении маятника от равновесного положения. При отклонении маятник начинает двигаться взад-вперед, совершая периодические колебания.

Период колебания математического маятника зависит от его длины и ускорения свободного падения. Формула для расчета периода малых колебаний математического маятника выглядит следующим образом:

T = 2π√(l/g)

Где:

• T — период колебаний маятника;
• l — длина нити или стержня маятника;
• g — ускорение свободного падения (приближенно равно 9,8 м/с²).

Таким образом, математический маятник является важным инструментом для изучения колебательных процессов и подтверждения законов физики. Его применение находит в различных научных и инженерных областях, а также в повседневной жизни.

Формулы и методы расчета периода малых колебаний

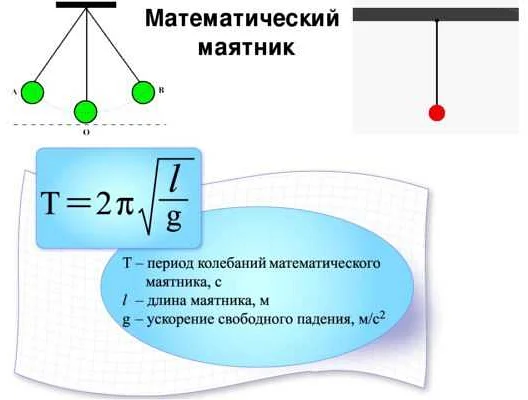
Период малых колебаний математического маятника может быть рассчитан с использованием различных формул и методов. Вот некоторые из них:

1. Формула периода математического маятника:

T = 2π√(l/g)

где T — период колебаний, l — длина подвеса маятника, g — ускорение свободного падения.

2. Формула периода физического маятника:

T = 2π√(I/mgh)

где T — период колебаний, I — момент инерции маятника, m — масса маятника, g — ускорение свободного падения, h — высота центра масс маятника над точкой подвеса.

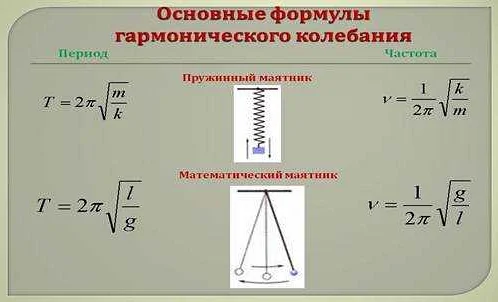
3. Формула периода гармонического осциллятора:

T = 2π√(m/k)

где T — период колебаний, m — масса осциллятора, k — коэффициент упругости.

4. Метод измерения периода колебаний:

Для измерения периода колебаний малого маятника можно использовать простой эксперимент. Необходимо отклонить маятник от положения равновесия на небольшой угол и засекать время, за которое маятник совершает определенное количество полных колебаний. Путем деления общего времени на количество колебаний можно получить период колебаний.

Эти формулы и методы позволяют рассчитывать период малых колебаний математического маятника и других систем, основанных на принципе гармонического осциллятора. Они являются важными в физике и науке в целом, и позволяют уточнить и предсказать результаты экспериментов и наблюдений.

Как можно определить период малых колебаний математического маятника?

Период малых колебаний математического маятника можно определить с помощью формулы, основанной на его физических характеристиках. Эта формула выражает зависимость периода колебаний от длины маятника и силы тяжести.

Формула для расчета периода малых колебаний математического маятника выглядит следующим образом:

Т = 2π√(l/g),

где T — период колебаний, l — длина маятника и g — ускорение свободного падения.

Для определения периода малых колебаний математического маятника необходимо знание его длины и значения ускорения свободного падения в данном месте. Длину маятника можно измерить с помощью линейки или мерной ленты. Ускорение свободного падения в разных местах Земли примерно равно 9,8 м/с², но точное значение можно узнать из специальных таблиц или измерений.

Подставив значения длины маятника и ускорения свободного падения в формулу, можно легко вычислить период малых колебаний математического маятника. Период колебаний представляет собой время, за которое маятник проходит полный цикл от точки равновесия до точки равновесия через одну крайнюю точку.

Знание периода малых колебаний математического маятника имеет практическое значение, так как позволяет предсказать время, которое потребуется маятнику для совершения определенного числа колебаний. Это особенно полезно в научных и технических расчетах, где точность и предсказуемость являются важными факторами.

Факторы, влияющие на период колебаний

Период колебаний математического маятника зависит от нескольких факторов:

Длина подвеса: Период колебаний прямо пропорционален квадратному корню из длины подвеса. Чем длиннее подвес, тем медленнее будет происходить колебание.

Масса груза: Масса груза не влияет на период колебаний математического маятника. Период колебаний зависит только от длины подвеса и силы тяжести.

Сила тяжести: Период колебаний обратно пропорционален квадратному корню из ускорения свободного падения. Чем больше сила тяжести, тем быстрее будет происходить колебание.

Начальные условия: Период колебаний может зависеть от начальных условий, таких как амплитуда колебания или начальная фаза. Однако, для малых колебаний, эти факторы имеют незначительное влияние.

Сопротивление среды: В наличии сопротивления среды, период колебаний будет зависеть от коэффициента затухания и механизма потери энергии. В идеальной среде без сопротивления, период колебаний будет постоянным.

Изучение этих факторов позволяет более точно предсказывать и оценивать период колебаний математического маятника и его поведение в различных условиях.

Какие факторы могут повлиять на период малых колебаний математического маятника?

Период малых колебаний математического маятника зависит от нескольких факторов, которые могут влиять на его значение. Важно учитывать эти факторы при расчете периода колебаний, чтобы получить более точные результаты.

Основные факторы, которые могут оказывать влияние на период малых колебаний математического маятника, включают:

Длина подвеса маятника	Длина подвеса математического маятника является основным фактором, определяющим его период. Чем длиннее подвес, тем больше будет период колебаний. Это связано с тем, что при большей длине подвеса маятник имеет больший путь, который он должен пройти за одно колебание.
Масса маятника	Масса математического маятника также влияет на его период колебаний. Чем больше масса маятника, тем меньше будет период колебаний. Это связано с тем, что более тяжелый маятник требует большей силы для изменения его положения, что замедляет его колебания.
Ускорение свободного падения	Ускорение свободного падения, которое обычно обозначается как g, также влияет на период малых колебаний математического маятника. Ускорение свободного падения зависит от местоположения на Земле и может незначительно различаться в разных точках. Чем больше ускорение свободного падения, тем меньше будет период колебаний.

Изучение этих факторов и их влияния на период малых колебаний математического маятника позволяет более точно предсказывать его поведение и использовать эту информацию при выполнении различных расчетов и экспериментов.

Применение формулы расчета периода малых колебаний в практике

Формула расчета периода малых колебаний математического маятника имеет широкое применение в различных областях науки и техники. Эта формула позволяет определить время, за которое происходит один полный оборот маятника вокруг своей оси.

Одним из основных применений этой формулы является измерение времени в физических экспериментах. Математический маятник используется для создания точного и стабильного временного интервала, что позволяет исследователям измерить длительность других явлений и процессов.

Формула также применяется в инженерии для решения задач динамики конструкций. Например, при проектировании мостов или зданий необходимо учитывать воздействие ветра или землетрясений. В таких случаях формула позволяет оценить возможные колебания и сделать конструкцию более устойчивой.

Еще одним применением формулы является определение частоты колебаний в электрических цепях. При проектировании и настройке электронных устройств необходимо знать, как быстро сигналы будут менять свое состояние. Формула расчета периода малых колебаний позволяет определить эту частоту и сделать правильные настройки.

Область примененияПример

Физика	Измерение времени в экспериментах
Инженерия	Оценка динамической устойчивости конструкций
Электроника	Определение частоты колебаний в электрических цепях

Применение формулы расчета периода малых колебаний позволяет решать различные задачи в науке и технике. Она является важным инструментом для измерения времени, анализа динамических процессов и определения частоты колебаний. Использование этой формулы позволяет улучшить точность и надежность исследований и разработок в различных областях.

Где и как используется формула расчета периода малых колебаний математического маятника?

Математический маятник представляет собой идеализированную модель, состоящую из массы, закрепленной на невесомой нерастяжимой нити или стержне. Период колебаний математического маятника определяется формулой:

T = 2π√(L/g)

где T — период колебаний маятника, L — длина нити или стержня, g — ускорение свободного падения.

Формула позволяет вычислить период колебаний математического маятника исходя из его физических параметров — длины нити или стержня и ускорения свободного падения. Также она позволяет проводить различные физические эксперименты, изучать зависимость периода колебаний от длины и ускорения свободного падения.

Формула используется в различных областях науки и техники, где изучаются колебательные процессы и системы. Например, в физике она применяется для расчета периода колебаний маятника при различных значениях его длины и в зависимости от ускорения свободного падения на разных планетах.

Формула также находит применение в инженерии, особенно в области проектирования маятниковых часов. Расчет периода колебаний математического маятника позволяет определить длину нити или стержня, необходимую для создания часов с заданным периодом колебаний.

Таким образом, формула расчета периода малых колебаний математического маятника находит широкое применение в науке и технике, где изучаются колебательные процессы и системы, а также в проектировании маятниковых часов и других устройств, основанных на принципе работы математического маятника.

Видео по теме:

Вопрос-ответ:

Какова формула для расчета периода малых колебаний математического маятника?

Формула для расчета периода малых колебаний математического маятника выражается следующим образом: T = 2π√(l/g), где T — период колебаний, l — длина математического маятника, g — ускорение свободного падения.

Каково значение ускорения свободного падения g?

Ускорение свободного падения g равно примерно 9,8 м/с² на поверхности Земли. Это значение может незначительно меняться в разных местах на Земле и зависит от высоты над уровнем моря, гравитационного поля и других факторов.

Что означает длина математического маятника l в формуле периода колебаний?

Длина математического маятника l в формуле периода колебаний представляет собой расстояние от точки подвеса до центра масс маятника. Она измеряется в метрах и является важным параметром для определения периода колебаний.

Влияет ли масса математического маятника на его период колебаний?

Масса математического маятника не влияет на его период колебаний. Формула для расчета периода малых колебаний не содержит массу маятника. Период колебаний зависит только от длины маятника и ускорения свободного падения.

В чем состоит физический смысл формулы периода малых колебаний математического маятника?

Формула периода малых колебаний математического маятника описывает зависимость между длиной маятника и его периодом колебаний. Чем длиннее маятник, тем медленнее будет его период колебаний. Формула позволяет предсказывать период колебаний для данного математического маятника и использовать эту информацию в различных приложениях и экспериментах.

Что такое период малых колебаний математического маятника?

Период малых колебаний математического маятника — это время, за которое маятник совершает одно полное колебание вокруг своей равновесной позиции.

Ограничения и предположения формулы

Формула расчета периода малых колебаний математического маятника основана на нескольких ограничениях и предположениях.

1. Малые амплитуды. Формула работает только для малых угловых отклонений маятника от положения равновесия. Если амплитуда колебаний становится слишком большой, формула может давать неточные результаты.

2. Условие безразмерности. Формула предполагает, что длина маятника является безразмерной величиной и не влияет на период колебаний. Это предположение справедливо только для идеализированного математического маятника, в котором нет сопротивления воздуха и других факторов, которые могут изменить период колебаний.

3. Идеальные условия. Формула предполагает, что маятник движется в вакууме без каких-либо внешних сил, таких как трение или сопротивление воздуха. В реальности маятники подвержены воздействию множества факторов, которые могут влиять на их период колебаний.

Несмотря на эти ограничения и предположения, формула расчета периода малых колебаний математического маятника является полезным инструментом для приближенного определения периода колебаний в идеальных условиях.

Какие ограничения и предположения существуют при использовании формулы расчета периода малых колебаний математического маятника?

Для использования формулы расчета периода малых колебаний математического маятника необходимо соблюдать определенные ограничения и предположения. В первую очередь, формула применима только для идеализированного математического маятника, то есть для объекта, который можно считать точечной массой, закрепленной на невесомой нерастяжимой нити.

Другим ограничением является предположение о том, что амплитуда колебаний малая. Формула периода малых колебаний применяется только при условии, что амплитуда колебаний маятника не превышает некоторого критического значения. Если амплитуда слишком большая, то формула становится неточной и не дает достоверных результатов.

Также важно отметить, что формула периода малых колебаний применима только для малых углов отклонения маятника от положения равновесия. Если угол отклонения слишком велик, то формула не будет давать точных результатов.

Наконец, формула расчета периода малых колебаний математического маятника предполагает, что нет учета внешних сил, таких как сопротивление воздуха или трение в опоре нити. В реальных условиях эти силы могут оказывать влияние на движение маятника и изменять его период.